Dass Ellipsen als ebene Schnitte durch Kegel auftreten, ist natürlich wohlbekannt. Hier soll es nicht um den Nachweis gehen, dass bei bestimmten Schnitten durch Kegel (hier immer als senkrechte Kreiskegel verstanden) Ellipsen als Schnittkurven entstehen. Wir wollen die Umkehrung untersuchen:
Gegeben sei eine Ellipse mit den Halbachsen a und b sowie ein Kegel. Wie muss man durch den Kegel schneiden, um die vorgegebene Ellipse zu erhalten ?
Welche Probleme stecken in dieser Fragestellung ?
- Geht das mit jedem Kegel ?
- Wo liegen der obere und der untere Einschnittpunkt ?
- In welchem Winkel muss man in den Kegel einschneiden ?
Hier ist ein Vorschlag, wie man den Kegel und die Schnittfläche in einem rechtwinkligen (x,y,z)-Koordinatensystem vereinfacht darstellen kann. Man skizziert in der oberen (x,z)-Halbebene ( z ≥ 0 ) einen ebenen Längsschnitt (also y = 0 ) durch den Kegel; dieser Schnitt soll durch die Mittelachse des Kegels verlaufen; die Spitze des Kegels soll in (0,0) liegen. In Bild 1 sieht man in beiden Skizzen die Ränder eines Kegel-Längsschnitts als schräge Linien. Es wurden zwei Skizzen angefertigt, um zu zeigen, wie die Öffnungswinkel der Kegel sowie die Kippwinkel (der Mittelachse gegenüber der z-Achse) variieren können. - Die Geraden parallel zur x-Achse stehen für den Schnitt durch den Kegel, der die vorgegebene Ellipse erzeugen soll.
Zur weiteren Vereinfachung kann man annehmen, dass a ≥ b ist und dass der Kegel aus einer senkrechten Lage (Mittelachse auf der z-Achse) nach rechts (also im Uhrzeigersinn) gekippt wird.
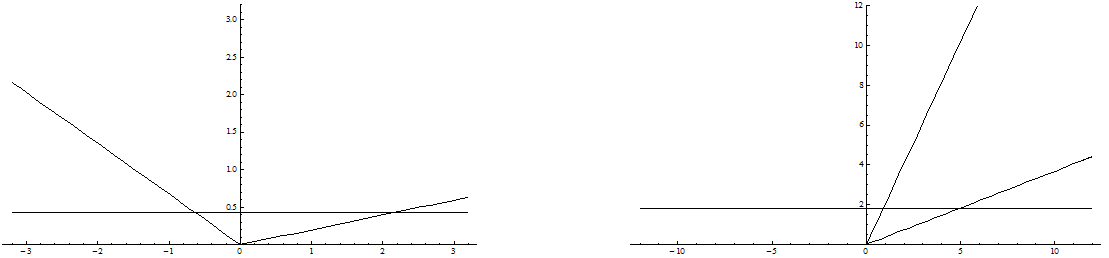
Bild 1
Noch mal zur Ausgangssituation: Gegeben sind a ≥ b und der halbe Öffnungswinkel des Kegels φ . Gesucht sind der Kippwinkel α und der Abstand d der achsenparallelen Geraden von der x-Achse; siehe Bild 2.
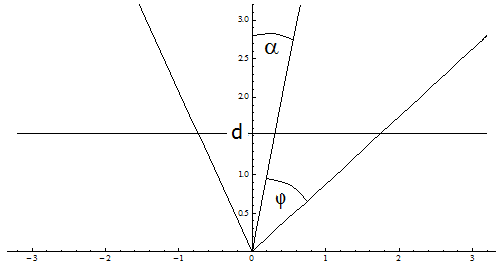
Bild 2 Ellipsenlängsschnitt mit Mittelachse
Man wird feststellen, dass es u.a. für den Einheitskegel mit φ = 45° immer eine Lösung gibt. Man erhält dann vereinfachte Formeln für α (wenn man eine trigonometrische Formel für den doppelten Winkel anwendet) und d .
Lösung