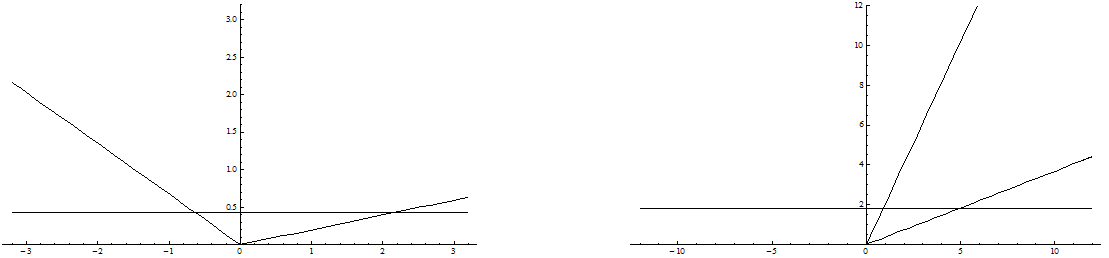Ellipse als Kegelschnitt
Die Lösung steht im unteren Teil der Seite.
Dass Ellipsen als ebene Schnitte durch Kegel auftreten, ist natürlich wohlbekannt. Hier soll es nicht um den Nachweis gehen, dass bei bestimmten Schnitten durch Kegel (hier immer als senkrechte Kreiskegel verstanden) Ellipsen als Schnittkurven entstehen. Wir wollen die Umkehrung untersuchen:
Gegeben sei eine Ellipse mit den Halbachsen a und b sowie ein Kegel. Wie muss man durch den Kegel schneiden, um die vorgegebene Ellipse zu erhalten ?
Welche Probleme stecken in dieser Fragestellung ?
- Geht das mit jedem Kegel ?
- Wo liegen der obere und der untere Einschnittpunkt ?
- In welchem Winkel muss man in den Kegel einschneiden ?
Hier ist ein Vorschlag, wie man den Kegel und die Schnittfläche in einem rechtwinkligen (x,y,z)-Koordinatensystem vereinfacht darstellen kann. Man skizziert in der oberen (x,z)-Halbebene ( z ≥ 0 ) einen ebenen Längsschnitt (also y = 0 ) durch den Kegel; dieser Schnitt soll durch die Mittelachse des Kegels verlaufen; die Spitze des Kegels soll in (0,0) liegen. In Bild 1 sieht man in beiden Skizzen die Ränder eines Kegel-Längsschnitts als schräge Linien. Es wurden zwei Skizzen angefertigt, um zu zeigen, wie die Öffnungswinkel der Kegel sowie die Kippwinkel (der Mittelachse gegenüber der z-Achse) variieren können. - Die Geraden parallel zur x-Achse stehen für den Schnitt durch den Kegel, der die vorgegebene Ellipse erzeugen soll.
Zur weiteren Vereinfachung kann man annehmen, dass a ≥ b ist und dass der Kegel aus einer senkrechten Lage (Mittelachse auf der z-Achse) nach rechts (also im Uhrzeigersinn) gekippt wird.
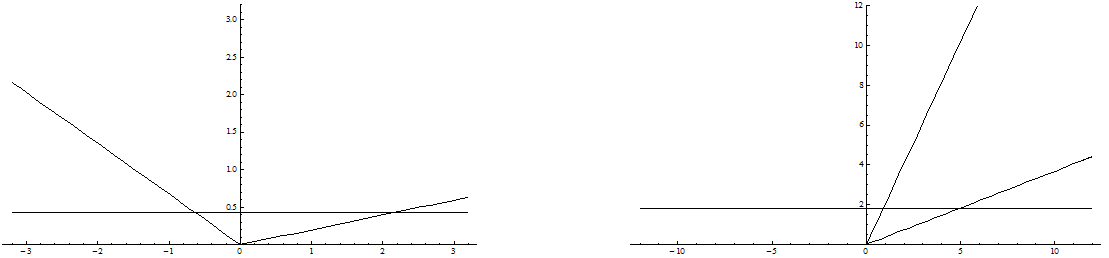
Bild 1
Noch mal zur Ausgangssituation: Gegeben sind a ≥ b und der halbe Öffnungswinkel des Kegels φ . Gesucht sind der Kippwinkel α und der Abstand d der achsenparallelen Geraden von der x-Achse; siehe Bild 2.
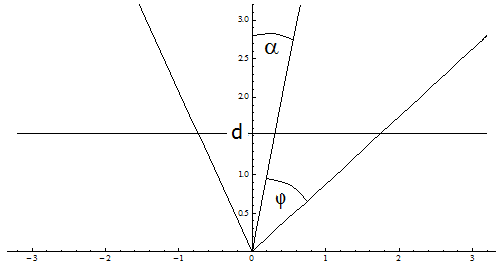
Bild 2 Ellipsenlängsschnitt mit Mittelachse
Man wird feststellen, dass es u.a. für den Einheitskegel mit φ = 45° immer eine Lösung gibt. Man erhält dann vereinfachte Formeln für α (wenn man eine trigonometrische Formel für den doppelten Winkel anwendet) und d .
Lösung
Die Winkel können die folgenden Werte annehmen: φ ∈ (0°, 90°) α ∈ [0°, 90°- φ)
Steht der Kegel senkrecht ( α = 0 ), so ist sein Schnitt parallel zur (x,y)-Ebene in der Höhe z ein Kreis mit Radius (tan φ)z . Also wird der Kegel durch die Gleichung beschrieben:
x2 + y2 = (rz)2 r = tan φ
Mit den Abkürzungen c = cos α und s = sin α erhält man den um α gekippten Kegel durch die Koordinatentransformation:
x → cx - sz
z → sx + cz
Dies führt auf die Gleichung für den gekippten Kegel (Längsschnitte in den Bildern 1 und 2):
(cx - sz)2 + y2 = r2(sx + cz)2
Nun macht man den Schnitt mit der Ebene, setzt also z = d , multipliziert die Gleichung aus und ordnet die Terme so, dass eine Ellipsengleichung entsteht; zur Abkürzung wird p = c2 - r2s2 gesetzt:
x2 - x·2csd(1+r2)/p + (csd(1+r2)/p)2 + y2/p = d2((r2c2-s2)/p + (cs(1+r2)/p)2)
quadr. Ergänzung quadr. Ergänzung
⇒ (x - csd(1+r2)/p)2 + y2/p = (dr/p)2
Es soll noch gezeigt werden, dass p positiv ist: c2 - r2s2
> cos2α - tan2(90°-α)sin2α = cos2α - cot2α sin2α = 0
Schreibt man die Ellipsengeichung in der Normalform (x - x0)2/a2 + y2/b2 = 1 , so folgt:
a2 =(dr/p)2 b2 = p·a2
a, b, r sind vorgegeben, also können wir d und α berechnen:
b2/a = dr ⇒ d = b2/(ra)
b2/a2 = p = cos2 α - r2(1-cos2 α) = (1+r2)cos2 α - r2 ⇒ α = arccos((b2/a2 + r2)/(1+r2))1/2
Also lässt sich jede Ellipse mit einem Kegelschnitt durch einen beliebigen senkrechten Kreiskegel erzeugen.
Wo wird in den Kegel eingeschnitten? In Bild 3 wurde der Kegel gegenüber den Bildern 1 und 2 wieder aufgerichtet. v1 und v2 beschreiben den oberen und unteren Einschnittpunkt als den jeweiligen Abstand von der Kegelspitze, entlang den Flanken des Kegels gemessen. h1 und h2 sind die entsprechenden Abstände entlang der Mittelachse.
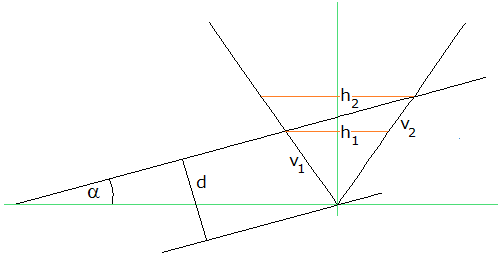
Bild 3
vi ergeben sich direkt aus Bild 2. Die auf der senkrechten Achse abgetragene Strecke der Länge d bildet nach links und nach rechts jeweils eine Kathete mit vi als Hypotenuse. Links: d/v1 = cos(φ-α) ; rechts: d/v2 = cos(φ+α) .
v1 = d/cos(φ-α) v2 = d/cos(φ+α)
Der Schnitt durch den Kegel in Bild 3 wird von der Geraden gebildet, die mit der x-Achse den Winkel α einschließt. Diese Gerade entsteht aus z = d durch Drehung um α im Gegenuhrzeigersinn, also durch z → -sx + cz . Für hi berechnen wir also die z-Koordinate des Schnittpunkts von -sx + cz = d und x = -rz bzw. x = rz :
h1 = d/(c+rs) h2 = d/(c-rs)
Damit ist das Problem gelöst. Bei einer gegebenen Ellipse und einem gegebenen Kegel ist der einfachste Weg, α und d nach den angegebenen Formeln zu berechnen und dann auf dem Mantel im Abstand v1 von der Spitze schräg im Winkel α einzuschneiden.
Wir wollen in den Bildern 4 und 5 zwei Beispiele zeigen - jeweils links den waagerechten Schnitt durch den gekippten Kegel, in der Mitte den aufgerichteten Kegel und rechts die Projektion der Ellipse auf die (x,y)-Ebene:

Bild 4 a = 1.9 b = 1.09 φ = 53° → α ≈ 29.53° d ≈ 0.4712 v1 ≈ 0.5137 v2 ≈ 3.6262 h1 ≈ 0.3091 h2 ≈ 2.1823
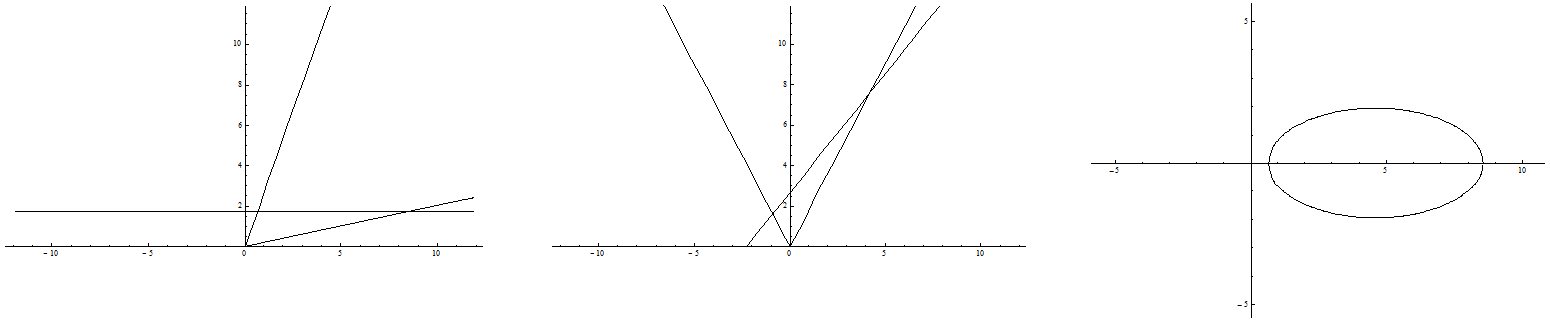
Bild 5 a = 3.95 b = 1.95 φ = 29° → α ≈ 49.52° d ≈ 1.7367 v1 ≈ 1.8543 v2 ≈ 8.7245 h1 ≈ 1.6218 h2 ≈ 7.6307
Einheitskegel
Da wir jede beliebige Ellipse für jeden Ellipsen-Öffnungswinkel 2φ erzeugen können, geht dies insbesondere für den Einheitskegel mit r = 1 , also φ = 45° . Wir erhalten mit den oben hergeleiteten Formeln für d und α sofort:
d = b2/a
sowie b2/a2 = 2cos2 α - 1 = cos 2α , also:
α = (arccos b2/a2)/2
Für v1 berechnen wir zunächst cos(45°- α) = (cos α + sin α)/√2 = (cos α + (1 - cos2α)1/2)/√2
Hier ist es es günstiger, mit α = arccos((b2/a2 + 1)/2)1/2 zu rechnen:
cos(45°- α) = ((1 + b2/a2)1/2 + (1 - b2/a2)1/2)/2
v1 = d/cos(45°- α) = 2d/((1 + b2/a2)1/2 + (1 - b2/a2)1/2) =
= (2b2/a)((1 + b2/a2)1/2 - (1 - b2/a2)1/2)/(2b2/a2) =
= a·((1 + b2/a2)1/2 - (1 - b2/a2)1/2)
v2 berechnet man analog und erhält:
v2,1 = a·((1 + b2/a2)1/2 ± (1 - b2/a2)1/2)
In Bild 3 erkennt man wegen φ = 45° sofort, dass
hi = vi /√2
Publiziert 2020-09-27 Stand 2017-04-23
voriges Problem | Liste aller Probleme mit Lösungen | nächstes Problem
Manfred Börgens |
zur Leitseite