Wir wollen Kreise in einer bestimmten Weise aneinanderreihen. Der Start des Verfahrens ist in Bild 1 zu sehen. Wir beginnen mit einem Kreis mit Radius 1 und Mittelpunkt (0,1) - Bild 1 zeigt davon nur die rechte Hälfte - und einem kleineren Kreis, der seinen Fußpunkt auf der positiven waagerechten Achse hat und den großen Kreis in einem Punkt tangential berührt.
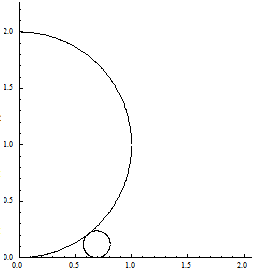
Bild 1
Die übrigen Kreise werden in zwei Schritten hinzugefügt. Im ersten Schritt werden rechts von den beiden Ausgangskreisen Kreise mit Fußpunkten auf der waagerechten Achse angefügt, die jeweils den kleineren Kreis links von ihnen und den ersten großen Kreis ganz links (mit Radius 1 ) tangential berühren. Dies sieht man in Bild 2. Offensichtlich kommt dieses Verfahren zu seinem Ende, wenn der Radius des zuletzt konstruierten Kreises ≥ 1 bzw. sein Fußpunkt ≥ 2 ist. Bei der Ausgangslage wie in Bild 1 kann man also nur zwei weitere Kreise konstruieren:
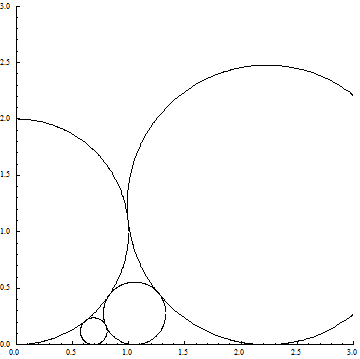
Bild 2
Der zweite Schritt verfährt analog zum ersten, aber jetzt werden die Kreise nach links angelegt. Hier ist keine Obergrenze für die Anzahl der Kreise zu erkennen. In Bild 3 sieht man drei von ihnen (in Orange), aber man hätte auch noch mehr skizzieren können. Die grünen Kreise stammen aus Schritt 1.
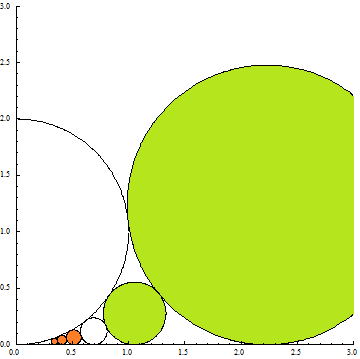
Bild 3
Für die weitere Diskussion wollen wir die Fußpunkte der Kreise benennen. Die x-Koordinaten der Fußpunkte der beiden Kreise in Bild 1 seien 0 und a , dabei sei a > 0 beliebig gewählt. Die Fußpunkte aus dem ersten Schritt seien tj , j = 1,2,... ; die Fußpunkte aus dem zweiten Schritt seien sj , j = 1,2,... ; die Nummerierung folgt der Reihenfolge der Konstruktion, siehe Bild 4.

Bild 4
Kleine Vorüberlegung
Geben Sie eine Schätzung ab - ohne zu rechnen - , wie groß der größte Kreis (ganz rechts) werden kann.
Aufgabe 1
Bestimmen Sie die Radien der konstruierten Kreise in Abhängigkeit von ihren Fußpunkten.
Die Radien, die zu tj gehören, sollen mit hj bezeichnet werden; die zu sj gehörigen mit gj . Zusätzlich setzen wir t0 = s0 = a . Für den Radius b des Kreises mit Fußpunkt a wird entsprechend h0 = g0 = b definiert. Die Mittelpunkte der Kreise (außer dem ganz linken) sind also (tj,hj) und (sj,gj) , j = 0,1,2,...
Aufgabe 2
Zeigen Sie, wie man einen neuen Kreis an die vorhandenen anlegt, d.h. bestimmen Sie tj+1 aus tj und sj+1 aus sj für j ∈ No (die entsprechenden Radien ergeben sich dann aus Aufgabe 1).
Aus der Berechnung ergibt sich auch, wie groß tj werden muss, damit das Verfahren abbricht. Ferner zeigt sich, dass es eine solche Beschränkung für sj nicht gibt, was uns anschaulich schon klar ist.
Aufgabe 3
Eine vollständige Induktion soll nun auf geschlossene Darstellungen der Fußpunkte tj und sj (und damit der Radien hj und gj ) führen. Diese hängen dann alle nur von a ab. Wie schon bei Aufgabe 2 ergibt sich, dass links vom Kreis mit Fußpunkt a unendlich viele Kreise liegen. Rechts davon lässt sich jetzt genau angeben, wieviele Kreise konstruiert werden können.
Aufgabe 4
Für welche a lässt sich die Summe aller Kreisflächen explizit berechnen - und mit welchem Ergebnis ?
Lösung