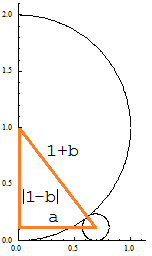Kreiskette

          Die Lösung steht im unteren Teil der Seite.

Wir wollen Kreise in einer bestimmten Weise aneinanderreihen. Der Start des Verfahrens ist in Bild 1 zu sehen. Wir beginnen mit einem Kreis mit Radius  1  und Mittelpunkt (0,1)  -  Bild 1 zeigt davon nur die rechte Hälfte  -  und einem kleineren Kreis, der seinen Fußpunkt auf der positiven waagerechten Achse hat und den großen Kreis in einem Punkt tangential berührt.



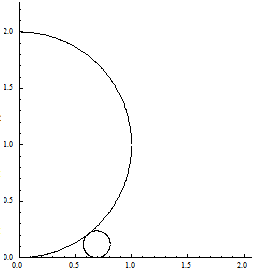
Bild 1

Die übrigen Kreise werden in zwei Schritten hinzugefügt. Im ersten Schritt werden rechts von den beiden Ausgangskreisen Kreise mit Fußpunkten auf der waagerechten Achse angefügt, die jeweils den kleineren Kreis links von ihnen und den ersten großen Kreis ganz links (mit Radius  1 ) tangential berühren. Dies sieht man in Bild 2. Offensichtlich kommt dieses Verfahren zu seinem Ende, wenn der Radius des zuletzt konstruierten Kreises  ≥ 1  bzw. sein Fußpunkt  ≥ 2  ist. Bei der Ausgangslage wie in Bild 1 kann man also nur zwei weitere Kreise konstruieren:



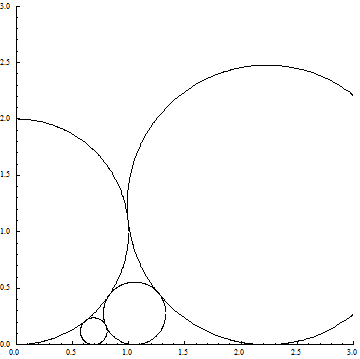
Bild 2

Der zweite Schritt verfährt analog zum ersten, aber jetzt werden die Kreise nach links angelegt. Hier ist keine Obergrenze für die Anzahl der Kreise zu erkennen. In Bild 3 sieht man drei von ihnen (in Orange), aber man hätte auch noch mehr skizzieren können. Die grünen Kreise stammen aus Schritt 1.



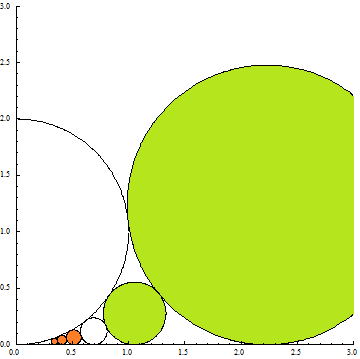
Bild 3

Für die weitere Diskussion wollen wir die Fußpunkte der Kreise benennen. Die  x-Koordinaten der Fußpunkte der beiden Kreise in Bild 1 seien  0  und  a ,  dabei sei  a > 0  beliebig gewählt. Die Fußpunkte aus dem ersten Schritt seien  t_j , j = 1,2,... ;  die Fußpunkte aus dem zweiten Schritt seien  s_j , j = 1,2,... ;  die Nummerierung folgt der Reihenfolge der Konstruktion, siehe Bild 4.




Bild 4


Kleine Vorüberlegung

Geben Sie eine Schätzung ab  -  ohne zu rechnen  - , wie groß der größte Kreis (ganz rechts) werden kann.


Aufgabe 1

Bestimmen Sie die Radien der konstruierten Kreise in Abhängigkeit von ihren Fußpunkten.

Die Radien, die zu  t_j  gehören, sollen mit  h_j  bezeichnet werden; die zu  s_j  gehörigen mit  g_j . Zusätzlich setzen wir  t₀ = s₀ = a . Für den Radius  b  des Kreises mit Fußpunkt  a  wird entsprechend  h₀ = g₀ = b  definiert. Die Mittelpunkte der Kreise (außer dem ganz linken) sind also (t_j,h_j) und (s_j,g_j) , j = 0,1,2,...


Aufgabe 2

Zeigen Sie, wie man einen neuen Kreis an die vorhandenen anlegt, d.h. bestimmen Sie  t_j+1  aus  t_j  und  s_j+1  aus  s_j  für  j ∈ N_o  (die entsprechenden Radien ergeben sich dann aus Aufgabe 1).
Aus der Berechnung ergibt sich auch, wie groß  t_j  werden muss, damit das Verfahren abbricht. Ferner zeigt sich, dass es eine solche Beschränkung für  s_j  nicht gibt, was uns anschaulich schon klar ist.


Aufgabe 3

Eine vollständige Induktion soll nun auf geschlossene Darstellungen der Fußpunkte  t_j  und  s_j  (und damit der Radien  h_j  und  g_j ) führen. Diese hängen dann alle nur von  a  ab. Wie schon bei Aufgabe 2 ergibt sich, dass links vom Kreis mit Fußpunkt  a  unendlich viele Kreise liegen. Rechts davon lässt sich jetzt genau angeben, wieviele Kreise konstruiert werden können.


Aufgabe 4

Für welche  a  lässt sich die Summe aller Kreisflächen explizit berechnen  -  und mit welchem Ergebnis ?

Lösung

Aufgabe 1

Bestimmen Sie die Radien der konstruierten Kreise in Abhängigkeit von ihren Fußpunkten.

Wir führen die Berechnung zunächst für den Kreis mit Fußpunkt  a  aus und bestimmen dessen Radius  b .  Der Mittelpunkt (a,b) dieses Kreises hat dann vom Mittelpunkt (0,1) des linken Kreises den Abstand  1+b  (siehe Bild 5), also gilt:

a² + (1-b)² = (1+b)²  ⇒  b = a²/4

Der Betrag um  1-b  in Bild 5 ist erforderlich, da  a  so gewählt werden kann, dass  b > 1  ist und deshalb die Kathetenlänge  b-1  beträgt; der rechte Winkel liegt in diesem Fall oberhalb von (0,1).



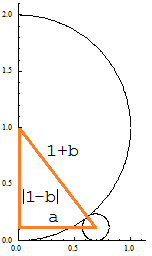
Bild 5

Auf gleiche Weise folgt   h_j = t_j²/4  und  g_j = s_j²/4 .


Aufgabe 2

Zeigen Sie, wie man einen neuen Kreis an die vorhandenen anlegt.

In Bild 6 soll der linke Kreis den Fußpunkt  t_j  haben und der rechte den Fußpunkt  t_j+1 . Die Katheten des eingezeichneten rechtwinkligen Dreiecks haben dann die Längen  t_j+1 - t_j  und  h_j+1 - h_j ;  die Hypotenuse zwischen den Mittelpunkten der Kreise hat die Länge  h_j+1 + h_j .



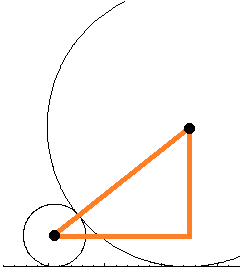
Bild 6

Mit dem Satz des Pythagoras und Aufgabe 1 erhält man (t_j+1 - t_j)² = 4 h_j+1·h_j = t_j+1²·t_j²/4 .

Daraus folgt  t_j+1 - t_j = t_j+1·t_j/2  und damit die rekursive Formel

t_j+1 = 2/(2/t_j - 1)

Daraus folgt mit Aufgabe 1

h_j+1 = 1/(1/√h_j - 1)²

In der Einleitung des Problems wurde schon festgestellt, dass  t_j+1  und  h_j+1  nur solange berechnet werden, wie  t_j < 2 ,  was äquivalent zu  h_j < 1  ist. Das ist anschaulich klar, deckt sich aber auch mit der Rekursionsformel für die  t_j.

Schreibt man die erste Rekursionsformel als  t_j+1 = t_j/(1-t_j/2) ,  so wird bestätigt, dass die  t_j  streng monoton wachsen, was ja aufgrund der Konstruktionsvorschrift des ersten Schrittes in der Aufgabenstellung auch verlangt wird. Wegen Aufgabe 1 wachsen auch die  h_j  streng monoton.

An dieser Stelle kann auch auf die  Kleine Vorüberlegung  vor Aufgabe 1 eingegangen werden. Für  t_j → 2  streben  t_j+1  und  h_j+1  gegen  +∞ .  Mit  a = t₀  nahe  2  lässt sich also schon im ersten Schritt ein beliebig großer Kreis erzeugen; Bild 7 zeigt dies für  a = 1,5 .



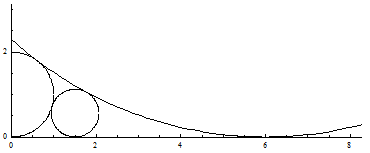
Bild 7


Bild 6 lässt sich auch für die Rekursionsformeln für  s_j  und  g_j  verwenden:

In Bild 6 soll nun der linke Kreis den Fußpunkt  s_j+1  haben und der rechte den Fußpunkt  s_j . Die Katheten des eingezeichneten rechtwinkligen Dreiecks haben dann die Längen  s_j - s_j+1  und  g_j - g_j+1 ;  die Hypotenuse zwischen den Mittelpunkten der Kreise hat die Länge  g_j + g_j+1 .

Mit dem Satz des Pythagoras und Aufgabe 1 erhält man (s_j - s_j+1)² = 4 g_j·g_j+1 = s_j²·s_j+1²/4 .

Daraus folgt  s_j - s_j+1 = s_j·s_j+1/2  und damit die rekursive Formel

s_j+1 = 2/(2/s_j + 1)

Daraus folgt mit Aufgabe 1

g_j+1 = 1/(1/√g_j + 1)²

Schreibt man die erste Rekursionsformel als  s_j+1 = s_j/(1+s_j/2) ,  so wird bestätigt, dass die  s_j  streng monoton fallen, was ja aufgrund der Konstruktionsvorschrift des zweiten Schrittes in der Aufgabenstellung auch verlangt wird. Wegen Aufgabe 1 fallen auch die  g_j  streng monoton.


Aufgabe 3

Eine vollständige Induktion soll auf geschlossene Darstellungen der Fußpunkte und der Radien führen. Diese hängen dann alle nur von  a  ab. Damit lässt sich angeben, wieviele Kreise rechts von  a  konstruiert werden können.


Wir setzen  t₀ = s₀ = a  in die Rekursionsformeln von Aufgabe 2 ein und erhalten sukzessive:

t₁ = 2/(2/a - 1)
t₂ = 2/(2/a - 2)
t₃ = 2/(2/a - 3)
...
t_j = 2/(2/a - j)
...

s₁ = 2/(2/a + 1)
s₂ = 2/(2/a + 2)
s₃ = 2/(2/a + 3)
...
s_j = 2/(2/a + j)
...

Die Formeln für  t_j  und  s_j  sind bisher nur Vermutungen, die aber leicht induktiv nachgewiesen werden:

t_j+1 = 2/(2/t_j - 1) = 2/(2/a - (j+1))

s_j+1 = 2/(2/s_j + 1) = 2/(2/a + (j+1))

Es folgt

h_j = 1/(2/a - j)²

g_j = 1/(2/a + j)²

Wir hatten festgestellt, dass  t_j+1  und  h_j+1  nur solange berechnet werden können, wie  t_j < 2 ,  was äquivalent zu  h_j < 1  ist.

t_j < 2  ⇔  j+1 < 2/a

Für  a < 2  lassen sich also  ⌈2/a - 1⌉  Kreise rechts von  a  bilden. Für  a ≥ 2  lassen sich rechts keine weiteren Kreise bilden.


Aufgabe 4

Für welche  a  lässt sich die Summe aller Kreisflächen explizit berechnen  -  und mit welchem Ergebnis ?

Die Flächeninhalte der Kreise betragen  π·h_j²  bzw.  π·g_j² .  Zu summieren sind also Terme der Form  π/(2/a ± j)⁴ .  Wir können die Summe  S  der Kreisflächen berechnen, wenn  2/a = m ∈ N  ist. Dann durchlaufen in Aufgabe 3 die Terme  2/a ± j  (auch für  j=0)  in  h_j  und  g_j  die natürlichen Zahlen, denn  h_jmax = h_2/a-1 = 1 .  Damit erhalten wir

S = π·Σ_n∈N n^-4

Hier haben wir es mit einem Funktionswert der Riemannschen Zeta-Funktion zu tun, nämlich ζ(4). Diesen Wert kann man leicht mit einem CAS berechnen:  Σ_n∈N n^-4 = π ⁴/90 .  In einem umfassenderen Kontext findet man dieses Ergebnis u.a. in MathWorld (Formel 73) und Abramowitz/Stegun (Formel 23.2.25) sowie in Particular Values (Wikipedia). Das führt uns zur Lösung dieser Aufgabe:

Für  a = 2/m  mit  m ∈ N  ist  S = π ⁵/90 ≈ 3,4 .

S  hängt also nicht von  m  ab !  Das ist auch leicht zu sehen, da die Fußpunkte aller Kreise für jedes  m  die absteigende Folge  2, 1, 2/3, 1/2, ..., 2/i, ..., 2/m = a, ..., 2/k, ...  durchlaufen.

Publiziert 2019-05-25          Stand 2019-01-03

voriges Problem   |   Liste aller Probleme mit Lösungen   |    nächstes Problem