Das folgende Dreieck ist ein diagonal halbiertes Quadrat der Seitenlänge 1 :
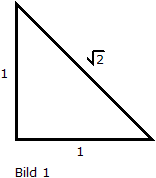
Es soll durch einen geraden Schnitt in zwei flächengleiche Teile zerlegt werden. Beide Teile haben dann den Flächeninhalt 1/4 :
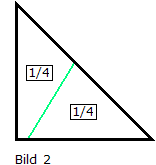
Wir suchen nun den kürzesten Schnitt. Dafür gibt es naheliegende Lösungsversuche, wie z.B. die symmetrische Teilung (Bild 3) oder seitenparallele Teilungen (Bilder 4 und 5) :
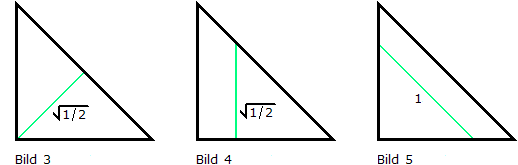
Die Teilung aus Bild 5 scheidet also aus. Wir haben zwei Teilungen mit einer Schnittlänge von √(1/2) ≈ 0.7071 gefunden (Bilder 3 und 4).
Gibt es eine kürzere Teilung ?
Lösung