Ein Mischungsproblem
Ich trinke gerne Apfelsaftschorle. Das ist ein Mischgetränk aus Apfelsaft und Mineralwasser. Ich möchte es mir selbst mischen und habe auch die Zutaten: Eine Flasche Apfelsaft und eine (beliebig) große Menge Wasser. Aber ich habe kein leeres Gefäß zum Mischen zur Hand. Pures Wasser mag ich nicht trinken, puren Apfelsaft schon eher. Also trinke ich einen Schluck aus der Saftflasche, fülle dann mit Wasser auf und schüttele die Flasche zur Durchmischung. Das wiederhole ich so lange, bis die Mischung halbe-halbe Saft und Wasser enthält.
Wir wollen annehmen, dass meine Schlucke gleich groß sind. Sie dürfen natürlich nicht größer als der halbe Flascheninhalt sein. Wenn ich irgendeine Größe meiner Schlucke vorgebe, kann ich nicht erwarten, dass ich exakt bei 50 % Wasser auskomme. Deshalb mache ich es andersherum: Ich frage mich, wie groß jeder Schluck sein muss, wenn ich die Anzahl der benötigten Schlucke vorgebe. Dazu kommen wir später noch. Die Hauptfrage dieses Problems ist die folgende:
- Wieviel muss ich trinken, bis nur noch die Hälfte des Apfelsafts in der Flasche ist?
Klar ist, dass ich bis dahin eine halbe Flasche Apfelsaft trinken muss. Die Frage lässt sich also darauf reduzieren, wieviel Wasser mit diesem Saft vermischt war. - Außerdem ist klar, dass ich genau soviel aus der Flasche trinke, wie insgesamt an Wasser in die Schorleflasche zugeführt wird.
Die Antwort hängt natürlich von der Anzahl n der Schlucke ab. Aus n lässt sich außerdem die Größe der Schlucke berechnen, wenn man ein Mischungsverhältnis von genau gleich viel Saft und Wasser erreichen will. Das Volumen der Flasche setzen wir der Einfachheit halber gleich 1 ; das Volumen eines Schlucks sei dann s .
- Bestimmen Sie s in Abhängigkeit von n .
Das müsste reichen, um die erste Frage zu beantworten.
Die Lösung ist vielleicht etwas unbefriedigend, weil sie n oder s enthält. Einsetzen von konkreten Werten von n oder s gibt aber schon einen guten Eindruck (viele finden das Ergebnis etwas überraschend). Wenn man davon ausgeht, dass ich in kleinen Schlucken trinke, müsste sich ein Näherungswert für die Menge aus der ersten Frage angeben lassen. Das wollen wir präzisieren:
- Bestimmen Sie den Grenzwert für die ausgetrunkene Menge (bis zum Erreichen der gewünschten Mischung) für n → +∞ bzw. s → 0 .
Dieses Mischungsproblem ist ein diskretes Problem, da das Trinken und Nachfüllen in einzelnen Schritten erfolgt. Es gibt ein verwandtes stetiges Problem, bei dem man vermuten kann (zu Recht, wie wir noch sehen werden), dass die Lösung mit dem eben bestimmten Grenzwert übereinstimmt. Die folgende schematische Skizze zeigt die "stetige Mischungsaufgabe":
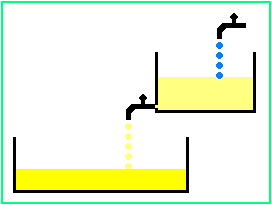
Was ist in der Skizze dargestellt? Wir befinden uns schon mitten im Mischprozess, d.h. der obere Behälter enthält bereits eine Mischung aus Saft und Wasser. Das Wasser kommt aus dem oberen Hahn. Wir stellen uns vor, dass die Mischung ständig gut umgerührt wird, so dass aus dem unteren Hahn die Schorle in dem Mischungsverhältnis ausläuft, dass man überall im oberen Behälter vorfindet. Er enthält immer die gleiche Menge Flüssigkeit, weil die beiden Hähne gleich weit geöffnet sind. - Die Analogie zum ursprünglichen diskreten Problem liegt auf der Hand: Der obere Behälter entspricht der Flasche, der untere enthält die "abgetrunkene" Menge. Der obere Hahn füllt das Wasser nach.
Hier stellt sich die analoge Frage zum diskreten Problem:
- Wieviel Wasser muss zugeführt werden, bis das Mischungsverhältnis im oberen Behälter halbe-halbe beträgt?
Die Lösung führt hier über eine einfache Differentialgleichung. Ein naheliegender Ansatz ist, die Funktion a(t) zu bestimmen, die den Apfelsaftanteil im oberen Behälter in Abhängigkeit von der Zeit (und damit vom Volumen des zugeführten Wassers) beschreibt. Für kleine Zeitintervalle h entspricht dann die Veränderung a(t+h)- a(t) näherungsweise der Veränderung im diskreten Problem bei einem Schluck. Für h → 0 führt das auf eine Differentialgleichung zur Bestimmung von a(t) .
Lösung
Publiziert 2011-05-20 Stand 2010-09-19
voriges Problem | Liste aller Probleme mit Lösungen | nächstes Problem
Manfred Börgens | zur Leitseite
