Wieviel Schatten spendet eine Mauer ?


Dies ist eine Aufgabe zum bevorstehenden Frühlingsanfang.

Eine lange Mauer begrenzt einen Garten in West-Ost-Richtung. Sie hat überall die gleiche Höhe. Immer wenn mittags die Sonne scheint, wirft die Mauer ihren Schatten in den Garten.

Wieviel Schatten spendet die Mauer im Garten am Frühlingsanfang im Laufe des Tages zwischen Sonnenaufgang und Sonnenuntergang ?

Man erhält natürlich das gleiche Ergebnis für den Herbstanfang. Für die anderen Tage des Jahres ist das Problem wesentlich schwieriger; man benötigt dafür Grundkenntnisse in Astronomie und sphärischer Trigonometrie. Aber es ist möglich, auch ohne Kenntnis der exakten Lösung den wesentlichen Unterschied zu Frühlings- und Herbstanfang zu erkennen. Insbesondere kann man daraus schließen, ob der Schatten zunächst (vormittags) wächst oder schrumpft. Dabei ist immer im Auge zu halten, an welchem Ort der Erde man sich befindet.

Jetzt kommt noch eine Zusatzfrage, die nicht mit der Schattenlänge, sondern mit der Schattendauer zu tun hat:
Wann ist die längste Schattendauer ?  Gefragt ist also nach dem Tag, an dem der Schattenwurf der Mauer in den Garten die längste Zeit anhält.

Lösung

Bild 1 zeigt, wonach gefragt ist:  t  ist die Schattenlänge der Mauer, gemessen als (rechtwinkliger) Abstand der Schattenkante vom Fuß der Mauer.



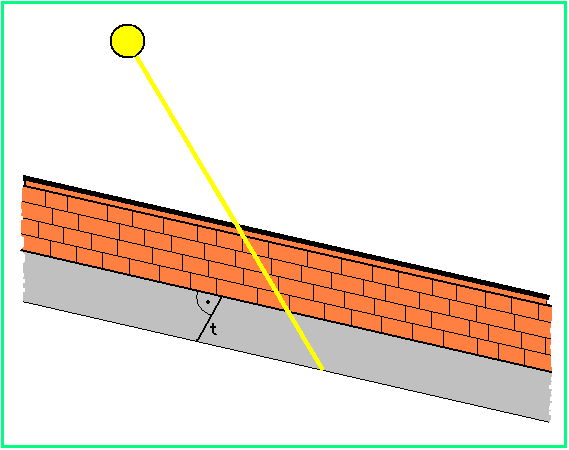
Bild 1

In Bild 1 steht die Sonne hinter der Mauer; der Schatten fällt also entweder in Nord- oder in Südrichtung in den Garten. Das kann sich nicht am Nord- oder Südpol abspielen, da es dort keine West-Ost-Richtung für die Mauer gibt. Am Frühlingsanfang kann die Mauer aber auch nicht auf dem Äquator stehen, weil sie dann gar keinen Schatten werfen würde. Steht die Mauer zwischen Äquator und Nordpol, so fällt der Schatten nach Norden, steht sie zwischen Äquator und Südpol, fällt der Schatten nach Süden. Aus Symmetriegründen wollen wir uns auf die Nordhalbkugel beschränken. Wenn man die Problemstellung genau liest, gibt es noch eine weitere Einschränkung. "Immer wenn mittags die Sonne scheint, wirft die Mauer ihren Schatten in den Garten." Dies wurde unabhängig vom Datum formuliert, soll also das ganze Jahr über gelten. Damit entfallen die Tropen, also die Zone zwischen den Wendekreisen, denn dort würde die Mauer ihren Schatten zeitweise nach Norden und zeitweise nach Süden werfen, jedenfalls nicht immer in den Garten hinein. Also befindet sich unsere Mauer zwischen nördlichem Wendekreis (Breitengrad  23,45° N ) und dem Nordpol. Für den Frühlingsanfang ist diese Einschränkung allerdings unerheblich.

Wir werden die Höhe der Mauer der Einfachheit halber  = 1  setzen. Andere Höhen wirken sich dann proportional auf die Schattenlänge aus. Der Schattenwurf hängt vom Höhenwinkel  h  der Sonne und von ihrer Himmelsrichtung  α  ab.

Zwei schematische Zeichnungen (Bild 2) erleichtern die Orientierung. In der linken Skizze betrachten wir statt der Mauer einen Pfahl der Höhe  1  mit der Schattenlänge  s , in der rechten Skizze wird der Zusammenhang zwischen  α, s  und  t  deutlich:


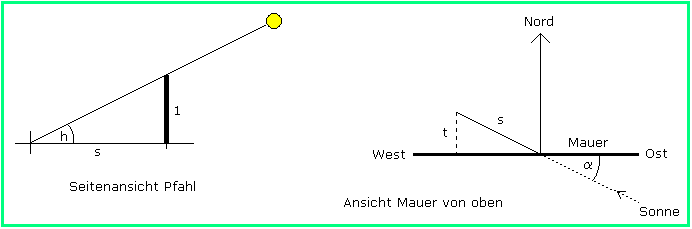
Bild 2

Der Winkel  α  beträgt  0° , wenn die Sonne im Osten steht,  90°  im Süden und  180°  im Westen. Nur das Intervall  (0°,180°)  kommt in Betracht, wenn der Schatten in den Garten fallen soll. Aus Bild 2 erhält man:

s = cot h   und   t = s · sin α , also zusammen

(1)   t = cot h · sin α

Ist der Breitengrad  φ  bekannt, auf dem die Mauer steht, und ist das Datum festgelegt (Frühlingsanfang), so muss sich  h  durch  α  ausdrücken lassen, so dass die Schattenlänge  t  nur noch von der einen unabhängigen Variablen  α  abhängt, also von der Himmelsrichtung der Sonne. Dazu benötigen wir ein wenig Kugelgeometrie. In Bild 3 betrachten wir die Sonnenbahn über einer halben Horizontebene. Dies ist eine geozentrische Darstellung, die aber die Verhältnisse zwischen Erde und Sonne richtig wiedergibt und geometrisch äquivalent ist zur heliozentrischen Darstellung. Bei der geozentrischen Darstellung steht der Beobachter auf dem Berührpunkt einer Tangentialebene der Erd"kugel". Aus seiner Sicht ist die Tangentialebene die Horizontebene und wird deshalb als Kreisfläche gezeichnet. Im Laufe eines Tages ändert sich die Entfernung der Sonne vom Beobachter nicht nennenswert, also lässt sich ihre Bahn auf einer Kugel mit dem Beobachter im Mittelpunkt beschreiben. (Der wahre Mittelpunkt ist natürlich der Erdmittelpunkt, aber der Durchmesser der Erde ist vernachlässigbar gegenüber dem Abstand Erde - Sonne.) Am Frühlingsanfang läuft die Sonne fast exakt durch die Äquatorebene, beschreibt also einen Großkreis auf der Kugel. Auch die Horizontebene schneidet die Kugel in einem Großkreis. Großkreise spielen in der Kugelgeometrie die Rolle der Geraden, da sie die kürzesten Verbindungen zwischen Kugelpunkten liefern ("Geodätische"), und für Dreiecke auf der Kugel, die durch Großkreisstücke begrenzt sind, gibt es trigonometrische Gesetzmäßigkeiten in Analogie zur Ebene.

In Bild 3 wurde verwendet, dass am Frühlingsanfang die Sonne genau im Osten aufgeht und genau im Westen untergeht. Der Auf- und Untergangswinkel hängt vom Breitengrad  φ  des Beobachters ab und beträgt  90°-φ .


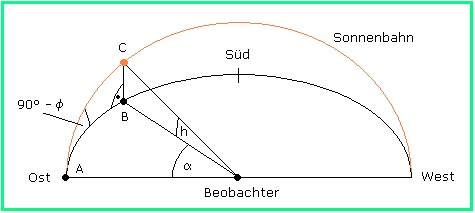
Bild 3

In Bild 3 sehen wir ein rechtwinkliges sphärisches Dreieck  ABC  auf der Kugel der Sonnenbahn.  A  ist der Punkt auf der Horizontebene, an dem die Sonne aufgeht.  C  stellt die Sonne an einem bestimmten Punkt im Tagesverlauf dar und  B  ihren "Fußpunkt" auf der Horizontebene, der in der gleichen Himmelsrichtung wie die Sonne liegt. Die Länge der Stücke von Großkreisen beschreibt man auf der Kugel durch die zugehörigen Mittelpunktswinkel (sofern nur die trigonometrischen Verhältnisse interessieren, aber nicht der Kugelradius). Das Kreisstück  AB  wird also durch  α  gemessen und  BC  durch  h . Wenn nun der Breitengrad des Beobachters und die Himmelsrichtung der Sonne vorgegeben werden, so sind von  ABC  eine Seite, nämlich  AB = α , und ein Winkel, nämlich  90°-φ  bei  A , bekannt; gesucht ist die Höhe der Sonne  BC = h . Diesen Fall schaut man in einer Formelsammlung für sphärische Trigonometrie nach und findet:

(2)   tan h = sin α · tan (90°-φ)

Aus (1) und (2) ergibt sich  t = 1/tan(90°-φ) ; dies lässt sich vereinfachen zu:

Wir haben eine interessante und elegante Lösung gefunden:

Beispiel :  Auf der geographischen Breite von Friedberg in Hessen,  φ = 50°20' N , wirft eine  1 m  hohe Mauer in W-O-Richtung bei Frühlingsanfang ganztägig einen Schatten von ca. 1,206 m . Am 20. März 2006 können Sie das experimentell überprüfen.


Zu den beiden anderen Fragen aus der Aufgabenstellung zunächst ein paar Vorüberlegungen. Nur am Frühlings- und Herbstanfang geht die Sonne genau im Osten auf und im Westen unter und steht genau 12 Stunden am Himmel. Im Winterhalbjahr, also zwischen Herbstanfang und Frühlingsanfang, ist diese Zeit kürzer, und die Sonne steht schon bei ihrem Aufgang hinter der Mauer (vom Ostpunkt Richtung Süden verschoben). Das bedeutet, dass der Schatten der Mauer bei Sonnenaufgang unendlich lang ist und mit steigender Sonne abnimmt. Dies lässt sich durch Beziehung (1) erhärten, die für alle Tage des Jahres gilt: Bei Sonnenaufgang ist  h = 0  und  α > 0 ; wir erhalten  lim t = ∞  für  h --> 0 . Wegen der Symmetrie zum Mittag ist es somit eine plausible (und die einfachste) Vermutung, dass die Schattenlänge eine Kurve etwa der folgenden Form beschreibt:


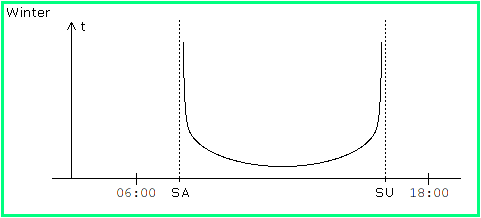
Bild 4

Wir werden noch sehen, dass diese Vermutung richtig ist.

Im Sommerhalbjahr wirft die Mauer bei Sonnenaufgang ihren Schatten in die "falsche" Richtung, also nicht in den Garten, denn ihr Aufgangspunkt liegt vom Ostpunkt aus Richtung Norden verschoben. Im Osten steht steht die Sonne erst später als 6:00 Uhr Ortszeit; zu diesem Zeitpunkt wirft die Mauer keinen Schatten. Wandert die Sonne weiter, wächst der Schatten allmählich. Dies lässt sich wieder durch Beziehung (1) erhärten: Wenn die Sonne im Osten steht, ist  h > 0  und  α = 0 ; wir erhalten  lim t = 0  für  α --> 0 . Wegen der Symmetrie zum Mittag ist es somit eine plausible (und die einfachste) Vermutung, dass die Schattenlänge eine Kurve etwa der folgenden Form beschreibt:


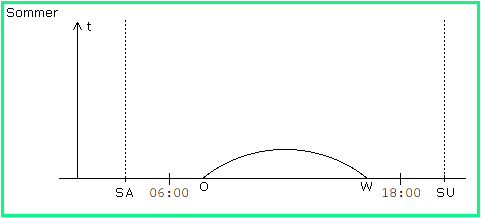
Bild 5

Wir werden noch sehen, dass auch diese Vermutung richtig ist.

Die beiden Kurven in Bild 4 und Bild 5 zeigen den wesentlichen Unterschied zum Frühlings- und Herbstanfang. Der Schatten der Mauer verändert sich im Lauf des Tages; winters ist er morgens sehr lang und schrumpft dann, sommers ist er morgens sehr kurz und wächst dann; abends beobachtet man die dazu symmetrischen Phänomene. Insbesondere folgt aus den bisherigen Überlegungen:

Die Schattendauer ist am längsten am Frühlings- und Herbstanfang, und zwar 12 Stunden.

Im Winterhalbjahr ist die Schattendauer verkürzt durch den späten Sonnenaufgang und den frühen Sonnenuntergang, im Sommerhalbjahr durch die spät liegende Oststellung und die früh liegende Weststellung der Sonne.

Damit sind die Fragen aus der Problemstellung beantwortet. Natürlich können wir ohne genaue Herleitung nicht wissen, ob die Gestalt der Kurven in Bild 4 und Bild 5 wirklich so einfach ist und tatsächlich die Extrema mittags auftreten. Wir haben uns ja bisher nur plausibel gemacht, wie sich die Kurven am linken und rechten Rand verhalten. Also benötigen wir für alle, die es genau wissen wollen, die allgemeine Formel für die Schattenlänge.

Zur Erinnerung: Aus Symmetriegründen soll nur die Nordhalbkugel mit Ausnahme des Nordpols betrachtet werden. Wir werden allerdings jetzt die Tropen und den Äquator mit einbeziehen.

Will man den Schattenwurf für das ganze Jahr mathematisch analysieren, so muss man das oben vorgestellte geozentrische Modell verallgemeinern. Nur bei Frühlings- und Herbstanfang läuft die Sonne auf einem Großkreis, ansonsten über den Breitenkreisen der Erde zwischen den Wendekreisen. Dies gilt zumindest in sehr guter Näherung; an einem bestimmten Tag des Jahres umläuft die Sonne einen Breitenkreis  δ  mit  -23°,45 ≤ δ ≤ 23°,45 , über dem sie von der Erde aus gesehen senkrecht steht (das gilt natürlich nur näherungsweise, da sich  δ  kontinuierlich und nicht in Tagessprüngen ändert). Im geozentrischen Modell läuft also die Sonne auf einer Kugel, in deren Mittelpunkt der irdische Betrachter steht und dessen Horizontebene die Kugel halbiert; die Neigung dieser Ebene hängt vom Breitengrad ab. Man kann also wieder, so wie weiter oben für den Frühlingsanfang dargestellt, den Schattenwurf mit Mitteln der sphärischen Trigonometrie berechnen. Da dies mit Hilfe einer einfachen Formelsammlung gelingt und wir es hier auch nicht mit der zentralen Frage in der Problemstellung zu tun haben, sollen nur die wesentlichen Ergebnisse angegeben werden. Aus Symmetriegründen reicht es, die erste Tageshälfte zu betrachten. Frühlings- und Herbstanfang, also  δ = 0° , wenn die Sonne über dem Äquator senkrecht steht, wurden bereits behandelt und entfallen jetzt. Für den Breitengrad  φ  des Beobachters betrachten wir  0° ≤ φ < 90° . Die Tageszeit  τ  wird auch in Grad angegeben mit  0° = Mitternacht,  90° = 6 Uhr,  180° = Mittag.

In der folgenden Tafel finden sich die wichtigsten Formeln zur Behandlung des allgemeinen Schattenproblems:

Damit ergeben sich die folgenden Schattenverläufe. Die Begründungen folgen hinter den Bildern 6 und 7.


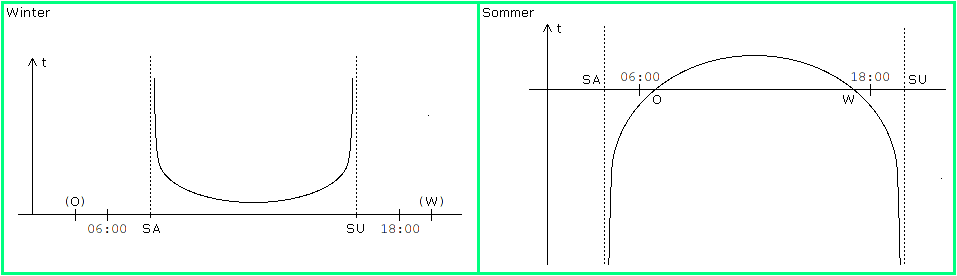
Bild 6

"Winter" heißt hier wieder  δ < 0  und "Sommer"  δ > 0 .  t < 0  bedeutet, dass der Schatten nach Süden fällt, also nicht in den Garten. Ost und West sind für das Winterhalbjahr eingeklammert, da die Sonne bei diesen Positionen unter dem Horizont steht. Für  |δ| ≥ φ  steht die Sonne den ganzen Tag über weder im Osten noch im Westen (auch nicht, wenn sie unter dem Horizont steht).

Ausnahme Winter:
φ + |δ| > 90°  : Sonne scheint gar nicht (Polarnacht).

Ausnahmen Sommer:
Eine wichtige Ausnahme zu Bild 6 tritt in der Polarregion auf. Ist  φ + δ > 90° , so steht die Sonne den ganzen Tag am Himmel. Bild 7 (links) zeigt dafür den Verlauf der Schattenlänge  t . Die zweite Ausnahme betrifft die Tropen. Ist  φ ≤ δ , so wirft die Mauer ihren Schatten nur nach Süden, und es gibt weder einen Ost- noch einen Westpunkt der Sonnenbahn (Bild 7 rechts). Dies ist z.B. dann der Fall, wenn man sich im Mai ein wenig nördlich des Äquators aufhält. Bei  φ = δ  berührt die Kurve die waagerechte Achse ( t = 0 ).


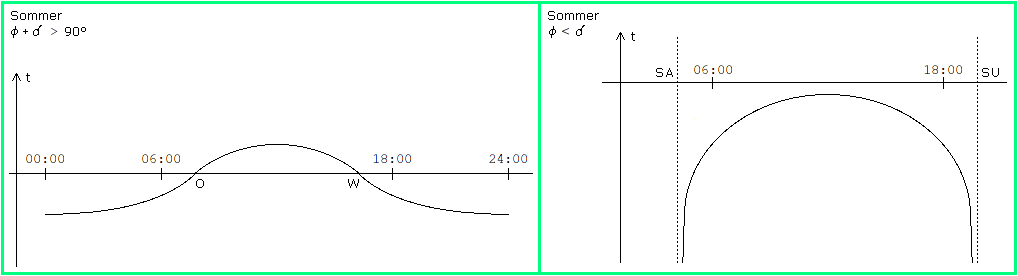
Bild 7


Die Kurven in den Bildern 6 und 7 ergeben sich aus den Formeln in der Tafel oben. Diese wollen wir kurz analysieren, unter Beachtung der Einschränkungen für die beteiligten Variablen oberhalb des Formelkastens. In den Graphen ist  τ  die unabhängige und  t  die abhängige Variable; vereinfacht schreiben wir deshalb für die Schattenlänge:

(6)    t = (a·cos τ + b) / (cos τ - a·b)

Dabei ist  a = tan φ  und  b = tan δ .

Für  a = 0  (Äquator) wird aus (6):

(7)    t = b / cos τ

Für  a > 0  lässt sich (6) umformen zu:

(8)    t = a·(1 + b·(a + 1/a)/(cos τ - a·b))

Winter  :  δ < 0
Die Gestalt des Graphen in Bild 6 (links) ergibt sich aus den folgenden Überlegungen. Zunächst folgt die zeitliche Reihenfolge Ostpunkt - 06:00 - Sonnenaufgang direkt aus (3) und (4).  t  hat in (6) keine Nullstellen, denn  a ≥ 0, b < 0  und  cos τ ≤ 0 . Der Nenner hat wegen (3) seine einzige Nullstelle bei Sonnenaufgang. Wegen (7) und (8) und  b < 0  nimmt  t  sein Minimum bei  τ = 180°  an, also um 12:00. Die Ausnahmen (kein Ostpunkt, kein Sonnenaufgang) ergeben sich mit (3) und (4).

Sommer  :  δ > 0
Die Gestalt des Graphen in Bild 6 (rechts) ergibt sich so: Die zeitliche Reihenfolge Sonnenaufgang - 06:00 - Ostpunkt folgt wieder direkt aus (3) und (4).  t  hat in (6) seine einzige Nullstelle für  cos τ = -b/a , d.h. im Ostpunkt. Der Nenner hat wegen (3) seine einzige Nullstelle bei Sonnenaufgang. Wegen (7) und (8) und  b > 0  nimmt  t  ein Maximum bei  τ = 180°  an, also um 12:00. Zur ersten Ausnahme (Bild 7 links): Ist  φ + δ > 90° , so hat der Nenner keine Nullstelle; man beachte, dass in diesem Fall auch das Minimum bei  τ = 0° , also um 00:00 zum Tragen kommt. Zur zweiten Ausnahme (Bild 7 rechts): Ist  φ < δ , so hat  t  in (6) keine Nullstelle und ist negativ; (4) zeigt, dass es keinen Ostpunkt gibt.


Bemerkung zur Schattendauer: Wegen der Aufgabenstellung ("Immer wenn mittags die Sonne scheint, wirft die Mauer ihren Schatten in den Garten.") hatten wir auf der Nordhalbkugel nur Mauern an der Südgrenze des Gartens in Betracht gezogen. Bild 7 zeigt aber einen interessanten Effekt für Mauern an der Nordgrenze. Hat man einen Garten nördlich des nördlichen Polarkreises, so wirft eine Mauer an der Nordgrenze des Gartens jedes Jahr während eines bestimmten Zeitraums (nämlich für  φ + δ > 90° ) einen Schatten nach Süden, der mehr als 12 Stunden pro Tag anhält und somit unser obiges Ergebnis relativiert. Gleiches gilt in den Tropen für die Zeit, wenn  φ < δ . Wann und wo ist die Schattendauer maximal? In der Polarregion (Bild 7 links) nimmt der Ostpunkt in (4) den maximalen Wert an, wenn  δ  möglichst groß und  φ  möglichst klein wird, also bei  δ = 23°,45  und  φ = 66°,55 , d.h. bei Sommeranfang am Polarkreis. In den Tropen (Bild 7 rechts) nimmt der Sonnenaufgang in (3) den minimalen Wert an, wenn  δ  und  φ  maximal werden, also  δ = φ = 23°,45 , d.h. bei Sommeranfang am Wendekreis (wegen der Nullstelle von  t  für  δ = φ  muss  φ = δ-ε  mit kleinem  ε  gewählt werden). In beiden Fällen erhalten wir einen Schattenwurf nach Süden mit der Dauer  13^h26'46'' .

Bemerkung zur Genauigkeit der Angaben: Der Schattenwurf einer Mauer ist gut beobachtbar und messbar. Die dazu in dieser Lösung gemachten Angaben sind für "Alltagsbeobachtungen" hinreichend genau, obwohl sie von idealisierten Bedingungen ausgehen (u.a. Kugelgestalt der Erde). In Wirklichkeit gibt es aber geringe Abweichungen: So ist z.B. die Sonne am Frühlingsanfang wegen des Linseneffekts der Atmosphäre etwas mehr als 12 Stunden sichtbar. Auch läuft die Sonne an diesem Tag nicht ganz exakt parallel zum Äquator, sondern beginnt ein wenig weiter südlich und endet ein wenig weiter nördlich. Dies alles beeinträchtigt die gefundenen Ergebnisse aber nicht nennenswert.

Bemerkung zu  δ :  δ ist eine Funktion der Jahreszeit und heißt Deklination. Wegen der elliptischen Erdbahn ist dies keine einfache Funktion. Für ein bestimmtes Datum kann man den Funktionswert in astronomischen Tabellenwerken nachlesen.

Eine ausführlichere Behandlung des Mauerschatten-Problems findet man in Blog # 3.


Kategorie: Geomathematik