Deutschland 1967  Michel 533  Scott 969     Armenien 2006  Michel 550  Scott 745     Ghana 1970  Michel 386A  Scott 375     Argentinien 1963  Michel 811  Scott 744



Die Mathematik der Zahnräder

Zahnräder enthalten viel Mathematik. Greifen zwei oder mehr Zahnräder ineinander, ergeben sich Übersetzungen als rationale Zahlen; weiter unten wird erklärt, wie dabei Kettenbrüche ins Spiel kommen. Insbesondere sollen Anwendungen angeführt werden, wie sie bei astronomischen Uhren vorkommen.  -  Die Form der Zähne bedarf der höheren Mathematik; für die Formung kommen u.a. Epizykloide und Hypozykloide zum Einsatz. Darauf wird auf dieser Seite nicht näher eingegangen; es gibt dazu informative Websites, z.B. auf Wikipedia.




Bild 1


Übersetzung

In der linken Skizze von Bild 1 greifen zwei Zahnräder ineinander. Eines davon bezeichnen wir mit Antriebsrad (oder Treiber), das andere mit Abtriebsrad. Das Antriebsrad wird durch eine äußere Kraft in eine Drehbewegung gesetzt und bewirkt dadurch die Drehung des Abtriebrades.

Definition der Übersetzung :  Antriebsrad hat  n  Zähne, Abtriebsrad hat  m  Zähne   →   Übersetzung  m:n

In der linken Skizze von Bild 1 hat das linke Zahnrad  36  Zähne, das rechte  8  Zähne. Sitzt der Antrieb links, ist die Übersetzung  8:36  oder  2:9 .  Das bedeutet, dass  2  Umdrehungen des linken Rads  9  Umdrehungen des rechten Rads bewirken.  -  Sitzt der Antrieb rechts, so ist die Übersetzung  36:8  oder  9:2 ;  9  Umdrehungen rechts bewirken  2  Umdrehungen links.

Bei zwei Zahnrädern drehen sich Antriebsrad und Abtriebsrad in entgegengesetzter Richtung. Will man das vermeiden, so setzt man ein weiteres Zahnrad zwischen die beiden, so wie in der rechten Skizze von Bild 1. Das mittlere Rad dient dabei sowohl dem Abtrieb als auch dem Antrieb. Die Zahnzahl des mittleren Rades ist unerheblich! Eine einfache, aber wichtige Regel lautet nämlich:

Zahnradgesetz A :  Die Übersetzung bleibt unverändert, wenn beliebig viele Zahnräder zwischen Antriebsrad und Abtriebsrad gesetzt werden.

Der Beweis muss nur für ein einziges zwischengeschaltetes Zahnrad geführt werden; induktiv folgt dann die Behauptung für mehrere Zwischenräder.  -  Sei also o.E. das linke von zwei Zahnrädern der Antrieb mit  p  Zähnen und das rechte der Abtrieb mit  r  Zähnen; die Übersetzung ist dann  r:p .  Nun soll zwischen den beiden ein Zahnrad mit  q  Zähnen eingefügt werden (in Bild 1 ist  p = 36, q = 22, r = 8).  Eine Umdrehung des linken Rades bewirkt  p/q  Umdrehungen des mittleren Rades; der Rest ist Dreisatz: Da  r  Umdrehungen des mittleren Rades  q  Umdrehungen des rechten Rades bewirken, werden von  p/q  Umdrehungen des mittleren Rades  (p/q)·(q/r)  Umdrehungen des rechten Rades bewirkt, was einer Übersetzung  r:p  entspricht.

Auf der Ghana-Marke sehen wir eine Übersetzung  1:1 .  Das rote und das grüne Zahnrad drehen sich gleichsinnig.  -  Die argentinische Marke zeigt zwei Zahnräder mit  8  und eines mit  16  Zähnen. Nimmt man das schwarze Rad als Antrieb und das weiße als Abtrieb, erhält man eine Übersetzung  1:2 ;  die Zahnzahl des roten Rades ist dafür unerheblich.


Verbundene Zahnräder

Setzt man zwei oder mehr Zahnräder auf dieselbe Achse und verbindet sie fest miteinander, so wollen wir von verbundenen Zahnrädern sprechen. Diese Technik wird u.a. eingesetzt, um bestimmte Übersetzungen mit relativ kleinen Zahnrädern zu konstruieren. In Bild 2 sehen wir ein Beispiel. Links ist ein Antrieb mit  36  Zähnen, der auf einen Abtrieb mit  22  Zähnen wirkt; dieser ist fest verbunden mit einem Rad mit  8  Zähnen, das wiederum als Antrieb für das ganz rechte Rad mit  17  Zähnen wirkt.



Bild 2

Wie wirkt in Bild 2 der ganz linke Antrieb auf den ganz rechten Abtrieb, d.h. welche Übersetzung wirkt zwischen den beiden? Im Zahnradgesetz B werden wir allgemein zeigen, wie die Übersetzung berechnet wird. Im Beispiel von Bild 2 ist die Übersetzung (22·17):(36·8) = 374:288 = 187:144 ;  man multipliziert dafür also die Zahnzahlen der Abtriebe (weiße Räder, erste Klammer) und die Zahnzahlen der Antriebe (grüne Räder, zweite Klammer).

Zahnradgesetz B :  Werden vier Zahnräder mit den Zahnzahlen (von links nach rechts) p, q, r, s  wie in Bild 2 so angeordnet, dass die mittleren beiden Räder verbunden sind, so ist die Übersetzung zwischen dem linken Rad (Antrieb) und dem rechten Rad (Abtrieb) (q·s):(p·r);  beide Räder drehen sich im selben Drehsinn.

Beweis: Macht das linke Rad  q·s  Umdrehungen, so drehen sich die beiden mittleren Räder  p·s-mal. Macht das nicht angetriebene mittlere Rad  p·s  Umdrehungen, so dreht sich das rechte Rad  p·r-mal.

Das Gesetz B lässt sich induktiv verallgemeinern auf mehr als vier Zahnräder. Das erste Produkt hat dann alle Zahnzahlen der Abtriebe als Faktoren, das zweite Produkt alle Zahnzahlen der Antriebe.


Anwendungsbeispiel: Metonischer Zyklus

Astronomische Uhren, wie man sie z.B. im Straßburger Münster oder am Prager Rathaus findet, benötigen komplizierte Übersetzungen, da sie den Lauf des Mondes und der Planeten in Beziehung zu unserer normalen Zeitmessung setzen. Im folgenden soll dies anhand eines eigenen Beispiels gezeigt werden, das bei der Berechnung des Osterdatums eine wichtige Rolle spielt, siehe Briefmarke # 106: Wir wollen einen Antrieb für den Metonischen Zyklus entwerfen.

Der Metonische Zyklus beruht auf einer astronomischen Zufälligkeit:  19  Sonnenjahre entsprechen recht genau  235  Mondmonaten (unter einem Mondmonat wollen wir die Zeit zwischen zwei Vollmonden verstehen). Nach  19  Jahren wiederholen sich also die Mondphasen. Der  19-jährige Zyklus wird abgezählt durch die (römischen) Goldenen Zahlen  I  bis  XIX .  Wie könnten bei einer astronomischen Uhr Uhrwerke für die Mondphasen und die Goldenen Zahlen hergestellt werden?

Zuerst muss festgelegt werden, welches Uhrwerk als Antrieb verwendet werden soll. Da sich der Metonische Zyklus über lange Zeiträume erstreckt, soll dafür die Jahresuhr gewählt werden, also die Uhr, deren Zeiger eine Umdrehung pro Jahr macht  -  solche Jahresuhren findet man auf den astronomischen Uhren z.B. zur Anzeige der Gedenktage der Heiligen und der Tierkreiszeichen.

Für die Monduhr benötigen wir also eine Übersetzung  19:235 .  Da  235  Zähne nicht leicht handhabbar bei der Herstellung und (wegen der Größe des Rades) im Betrieb sind, erinnert man sich an Gesetz B und macht die Zerlegung  235 = 47·5 .  Da  5  Zähne für ein Zahnrad zu wenig sind und sich außerdem  19  nicht zerlegen lässt, erweitert man mit einer nicht zu großen Zahl; wir wählen  8  als Faktor:  19:235 = (8·19):(47·40).  Diese Übersetzung sieht man in Bild 3; links sitzt die Jahresuhr als Antrieb, rechts die Monduhr als Abtrieb.



Bild 3    Übersetzung  19:235

Für die Goldenen Zahlen benötigt man ein Uhrwerk, dessen Zeiger eine Umdrehung in  19  Jahren vollführt. Eine mögliche Erweiterung der Übersetzung  19:1  ist  19:1 = (19·49):(7·7) .  Ausgehend von Bild 3 soll die Uhr für die Goldenen Zahlen nach links angebaut werden. Also wird auf das Jahresrad mittig ein  7-er-Rad montiert, das ein  49-er-Rad antreibt; auf dieses wird ein  7-er-Rad montiert, das ein  19-er Rad ganz links antreibt zur Anzeige der Goldenen Zahl. In der Praxis sind  7  Zähne eher etwas zu wenige; evtl. müsste man mit größeren Faktoren als  7  bzw.  49  arbeiten. In Bild 4 sieht man im oberen Teil, wie das Jahresrad (in der Mitte) nach rechts die Monduhr (wie in Bild 3) und nach links die Uhr für die Goldenen Zahlen antreibt. Im unteren Teil sind die zugehörigen Zifferblätter zum Antrieb (Jahresuhr mit Monaten) und zu den beiden Abtrieben (Goldene Zahlen und Monduhr mit Mondphasen) zu sehen.



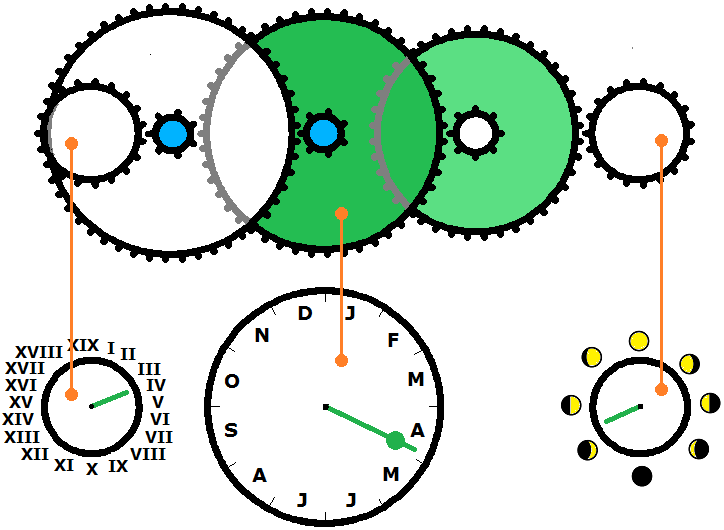
Bild 4    Antrieb über großes Rad in der Mitte, Übersetzung nach ganz rechts  19:235 ,  Übersetzung nach ganz links  19:1


Verwendung von Kettenbrüchen für Übersetzungen

Leonhard Euler zeigte, dass jede rationale Zahl durch einen endlichen regulären Kettenbruch dargestellt werden kann (den man z.B. mit Hilfe des euklidischen Algorithmus berechnet). Die Kettenbruchentwicklung erlaubt Näherungen von Brüchen mit großen Zählern und Nennern durch einfachere Brüche. Bei astronomischen Uhren wird von dieser Möglichkeit Gebrauch gemacht. Will man etwa das Verhältnis der Umlaufzeiten der Erde und eines anderen Planeten um die Sonne möglichst exakt darstellen, erhält man in der Regel einen komplizierten Bruch, der Zahnräder mit extrem vielen Zähnen erfordern würde. Man sucht also einfachere Brüche  -  für kleinere Zahnräder  - , die den ursprünglichen Bruch hinreichend genau approximieren. Diese Methode kann ergänzt werden durch geeignete Erweiterungen der Brüche. Beides  -  Kettenbruch und Erweiterung kombiniert  -  lässt sich am Beispiel der Übersetzung  19:235  in der Monduhr (siehe Bild 3) zeigen:

Kettenbruchentwicklung für den Metonischen Zyklus  19:235
    1:12   (Fehler:  3,07 % ;  zu lang)
    2:25   (Fehler:  1,05 % ;  zu kurz)
    3:37   (Fehler:  0,28 % ;  zu lang)
    8:99   (Fehler:  0,05 % ;  zu kurz)

Für eine direkte Umsetzung in Zahnräder kommt keiner dieser Brüche in Frage. Die ersten drei Brüche haben bei einem der Zahnräder maximal  3  Zähne; außerdem ist der Fehler für eine präzise Uhr zu hoch. Der Bruch  8:99  ist für eine Übersetzung noch am ehesten geeignet; hier würde dem Vorteil, dass man mit  2  Zahnrädern auskommt (gegenüber  4  Zahnrädern in Bild 3), der Nachteil entgegen stehen, dass man  99  Zähne benötigt (gegenüber  47  in Bild 3) und außerdem einen nicht unerheblichen Fehler in Kauf nehmen muss. Aber eine Erweiterung kann zu einer guten Faktorzerlegung führen:

8:99 = 64:792 = (8·8):(36·22)

Diese Übersetzung sieht man in Bild 5; sie könnte die Übersetzung in Bild 3 ersetzen. Man käme dann mit deutlich kleineren Zahnrädern aus, würde aber einen Fehler von  0,05 %  in Kauf nehmen müssen.

In Bild 5 ist der linke Treiber wieder eine Jahresuhr für die durchschnittliche Jahreslänge; mit den vier Zahnrädern erhält man wieder eine Monduhr (rechtes Zahnrad, eine Umdrehung von Vollmond zu Vollmond). Der linke Treiber hat  36  Zähne und treibt ein Zahnrad mit  8  Zähnen an; dieses ist verbunden mit einem zweiten Treiber mit  22  Zähnen, der das rechte Zahnrad mit  8  Zähnen antreibt.



Bild 5    Übersetzung  8:99


Die Darstellungen der Zahnräder auf dieser Seite sind nur schematisch, um die mathematischen Übersetzungsprinzipien zu erläutern. In der Praxis haben die Uhrmacher viele geniale technische Verbesserungen und Vereinfachungen erfunden.

Publiziert 2020-04-27          Stand 2019-05-29