deutsche Version

Parabola in a Square


We define the quadratic polynomial  f  by  f(x) = x² + b^.x + c  with  b,c ∈ R .

Which constants  b,c  suit the constraint  f: [-1,1] → [-1,1] ?

Hence, we are looking for all parabolas  f(x) = x² + b^.x + c ,  whose graph for  x ∈ [-1,1]  lies completely in the square  [-1,1]² .

Solution

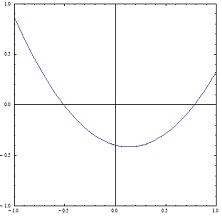
|b| ≤ 1  and  |c| ≤ 1  are shown easily:  f(0)= c  yields  |c| ≤ 1 ;    f(-1)= 1 - b + c ∈ [-1,1]  and  f(1)= 1 + b + c ∈ [-1,1]  yield  2b = f(1)-f(-1)∈ [-2,2] .

The parabolas in question are convex and have a strict absolute minimum. Hence, only two conditions must be considered:

a)  Both boundary values of the parabola must lie in  [-1,1] .  We want to find  b  and  c  with  f(-1)∈ [-1,1]  and  f(1)∈ [-1,1] .

b)  We shall prove that the minimum of the parabola has the coordinate  x = x_extr ∈ [-1/2, 1/2]  with  f'(x_extr) = 0 .  Hence, the second condition is  f(x_extr) ∈ [-1,1] .

To a)

We already know  |b| ≤ 1  and  |c| ≤ 1 .

(1)   f(1) ≤ 1  ⇔  1 + b + c ≤ 1  ⇔  c ≤ -b

(2)   f(1) ≥ -1  ⇔  1 + b + c ≥ -1 .  This is always true because  b ≥ -1  and  c ≥ -1 .

(3)   f(-1) ≤ 1  ⇔  1 - b + c ≤ 1  ⇔  c ≤ b

(4)   f(-1) ≥ -1  ⇔  1 - b + c ≥ -1 .  This is always true because  b ≤ 1  and  c ≥ -1 .

(1) - (4) yield

(5)   c ≤ -|b| .  This implies  c ≤ 0 .



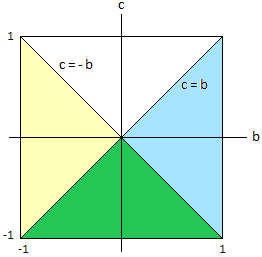
Figure 1

In figure 1 the blue-green region corresponds to  c ≤ b ,  the yellow-green region corresponds to  c ≤ -b .  The green intersection of the two regions contains all pairs (b,c) with  c ≤ -|b| ;  for these pairs the boundary values of the parabola lie in  [-1,1] .

To b)

Which pairs (b,c) in the green region of figure 1 belong to a parabola with minimum value in  [-1,1] ?

The first step is the proof that the absolute minimum of the parabola has the coordinate  x = x_extr ∈ [-1/2, 1/2] :

f'(x) = 2x + b = 0  ⇔  x = -b/2

x_extr = -b/2 ∈ [-1/2, 1/2]  and  f(x_extr) = -b²/4 + c ≤ 0 .  (5) implies that the minimum of the graph lies in the lower half of the real plane.

For the pairs (b,c) in the green region in figure 1 the condition  f(x_extr) ∈ [-1,1]  is equivalent to  -b²/4 + c ∈ [-1,0]  or  b²/4 - 1 ≤ c ≤ b²/4 .  But  c ≤ b²/4  is always true because  c ≤ 0 . Hence we get:

(6)   c ≥ b²/4 - 1 

Which  b  meet the condition (6) ?  Have a look at figure 2. There the graph of  c = b²/4 - 1  is the lower border of the green region. This graph does not stretch to  b = 1  or  b = -1  because  c ≤ -|b| (see (5) and the green region in figure 1). This means we have to find the intersections of  c = b²/4 - 1  and  c = -|b| .  For the intersection on the right with  b > 0  we get  b²/4 - 1 = -b  ⇔  b = √8 - 2 .  The symmetry of figure 2 gives the result:

(7)   |b| ≤ 2(√2 - 1) ≈ 0,8284


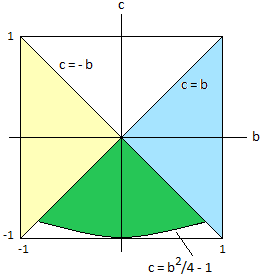
Figure 2

We conclude from (5), (6) and (7):

|b| ≤ 2(√2 - 1)     c ∈ [b²/4 - 1, -|b|]

The corresponding pairs (b,c) are shown as the green region in figure 2.


Example:  For  b = 1/2  all  c ∈ [-15/16, -1/2]  meet the conditions. One of the corresponding parabolas is  f(x) = x² + x/2 - 3/4  whose graph is shown in figure 3.



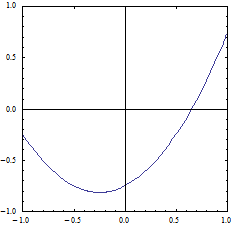
Figure 3


For a similar problem see Mathematical Excalibur 1/2, problem 6.