deutsche Version

Cutting up rectangles

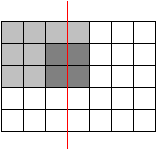
A rectangle is divided in  n·m  squares of equal size, like a matrix with  n  rows and  m  columns. By straight cuts from border to border, along the sides of the squares, the rectangle shall be completely cut up, leaving  n·m  separate squares. The following picture shows for  n = 4  and  m = 6  the start and the end of the procedure and in the middle a possible situation after several cuts.



We want to determine the minimum number of cuts. Two different ways of cutting will be discussed:

A :  It is not allowed to cut through more than one piece at a time. (Pieces may not be stacked or laid alongside each other before cutting.)

B :  Before each cut pieces may be stacked or laid alongside each other, allowing cuts through more than one piece.

The following picture shows three pieces in a stack:


This cut (red) is legal in variant  B , not in variant  A .


If you happen to have the right idea for variant  A  you will easily find the solution, without any computation. But you can also find the solution by testing the possible ways to cut up small rectangles; the rule for determining the minimum number of cuts will become evident.

Concerning variant  B  only this shall here be said: The intuitive idea for fastest cutting is the best one.


Solution