deutsche Version

Cutting up rectangles

A rectangle is divided in  n·m  squares of equal size, like a matrix with  n  rows and  m  columns. By straight cuts from border to border, along the sides of the squares, the rectangle shall be completely cut up, leaving  n·m  separate squares. The following picture shows for  n = 4  and  m = 6  the start and the end of the procedure and in the middle a possible situation after several cuts.



We want to determine the minimum number of cuts. Two different ways of cutting will be discussed:

A :  It is not allowed to cut through more than one piece at a time. (Pieces may not be stacked or laid alongside each other before cutting.)

B :  Before each cut pieces may be stacked or laid alongside each other, allowing cuts through more than one piece.

The following picture shows three pieces in a stack:


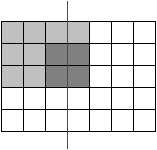
This cut (red) is legal in variant  B , not in variant  A .


If you happen to have the right idea for variant  A  you will easily find the solution, without any computation. But you can also find the solution by testing the possible ways to cut up small rectangles; the rule for determining the minimum number of cuts will become evident.

Concerning variant  B  only this shall here be said: The intuitive idea for fastest cutting is the best one.

Solution

Variant  A

You can try small numbers  n  and  m  in order to guess a general rule for the number  s  of cuts needed. A certain supposition will quickly arise: You need one cut less than the number of squares,  s = n·m - 1 . And it does not matter where you cut !  This (experimental) observation may give you the inspiration for the following very fine proof :  Every cut lets the number of separate pieces increase by one. You start with one piece and finish with  n·m  pieces. So we get :

Variant  B

Ask a bright child !  She or he will make the obvious and correct cut and divide the rectangle in two equal or nearly equal parts. This can be iterated. After each cut only one half resp. the (slightly) bigger piece stays in consideration because the other part can be put on top of the first. A sequence of rectangles with fast decreasing area results from this procedure :


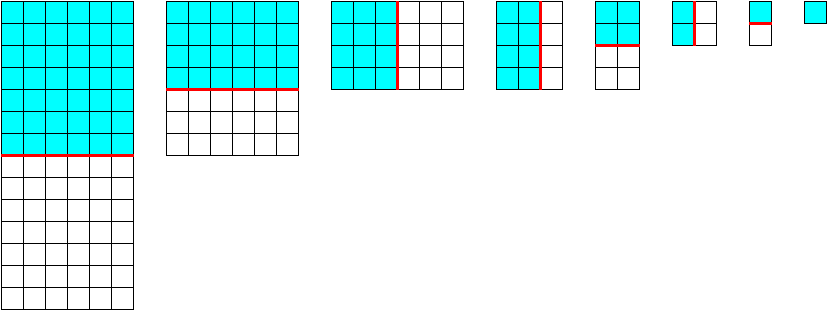
                                              Sequence of "round-up-halvings"


A "round-up-halving" will describe a straight cut through a rectangle with  k  "bars" (bars are rows or columns) which leaves an equal or smaller part with  [k/2]  bars. This was demonstrated in the picture above.   [·]  stands for the rounding-down of real numbers to natural numbers. So if  k  is even we cut in two halves with  k/2  bars each. If  k  is odd the larger part has  [k/2] + 1  bars (this is the rounding-up) and the smaller part has  [k/2]  bars. The smaller (or equal) remaining rectangle plays no role in the following cuts as we can put it on top of the larger (or equal) part. The whole procedure becomes easier if we leave the upper left square in its place and cut off the bars from the right (bars = columns) or from below (bars = rows) as in the picture. Then every cutting procedure ends with the upper left square.

This is the optimal procedure, and we will prove it. Any other cutting than the round-up-halving would leave a larger rectangle and obviously yield at least the same number of further cuts. It should be observed that the order of the cuttings (horizontal - vertical) is irrelevant because every horizontal cut leaves the vertical cutting lines untouched and vice versa.

How many cuts are needed ?  For  n = 2^r  rows we have to make  r  cuts; each of these cuts exactly results in two halves. For  2^r-1 < n < 2^r  we also need  r  cuts for the rows because  r-1  round-up-halvings leave  n/2^r-1  rows at least, and  n/2^r-1 > 1 . The same reasoning applies for the columns when we replace  n  by  m .

This can be expressed as follows: If  n  is a power of  2 , say  n = 2^r , we need  r = log₂n  horizontal cuts. If  n  isn't a power of  2  we take the nearest power of  2  above  n ; its exponent is the number of cuts. The analogous formula applies to the  m  columns. We add the numbers of horizontal and vertical cuts to obtain  s  and use  <·>  for the rounding-up of real numbers to natural numbers: