Zerlegung von Rechtecken
Die Lösung steht im unteren Teil der Seite.
Ein Rechteck sei in n·m gleich große Quadrate eingeteilt, wie eine Matrix mit n Zeilen und m Spalten. Durch gerade Schnitte von Rand zu Rand des Rechtecks, entlang der Quadratseiten, soll das Rechteck vollständig in die n·m Quadrate zerlegt werden. Im folgenden Bild sieht man für n = 4 und m = 6 die Anfangs- und Endlage und dazwischen eine Situation nach einigen Schnitten.

Diese Zerlegung soll mit möglichst wenigen Schnitten erfolgen. Dabei gibt es zwei Varianten:
A : Es ist nicht erlaubt, vor einem Schnitt zwei oder mehrere Teilstücke über- oder nebeneinander zu legen.
B : Bei jedem Schneiden dürfen beliebig viele Teilstücke über- oder nebeneinander gelegt werden, um sie gemeinsam mit einem Schnitt teilen zu können.
Das folgende Bild zeigt drei übereinandergelegte Teilstücke:
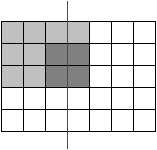
Dieser Schnitt (rot) ist in Variante B erlaubt, in Variante A dagegen nicht.
Wenn man bei Variante A die richtige Idee hat, findet man die Lösung sofort und ohne zu rechnen. Aber es geht auch ohne Geistesblitz, indem man verschiedene Schnittreihenfolgen bei kleinen Rechtecken ausprobiert; man erkennt schnell die Gesetzmäßigkeit.
Zu Variante B sei nur gesagt, dass die intuitive Idee für das schnellste Teilen die richtige ist.
Lösung
Variante A
Mit kleinen n und m kann man schnell ausprobieren, wieviel Schnitte s man benötigt. Auf diese Weise stellt sich die Vermutung ein, dass man einen Schnitt weniger braucht als die Anzahl der Quadrate, also s = n·m - 1 Schnitte. Außerdem stellt man fest, dass es offenbar unerheblich ist, in welcher Weise und Reihenfolge man schneidet. Diese Beobachtung führt uns zum Beweis : Bei jedem Schnitt erhöht sich die Anzahl der Einzelteile um eins. Man benötigt also immer, egal wie man die Schnitte ausführt, gleich viele Schnitte, nämlich:
Variante B
Stellen Sie diese Aufgabe einem aufgeweckten Kind! Es wird spontan das Naheliegende und Richtige tun, nämlich das Rechteck in zwei (annähernd) gleich große Stücke teilen und mit diesem Verfahren bis zum Ende fortfahren. Nach jedem Schnitt braucht man nur eine Hälfte bzw. das größere Stück für die folgenden Schnitte zu beachten, denn auf dieses darf man das andere Stück legen. So entsteht eine Folge von immer kleineren Rechtecken:
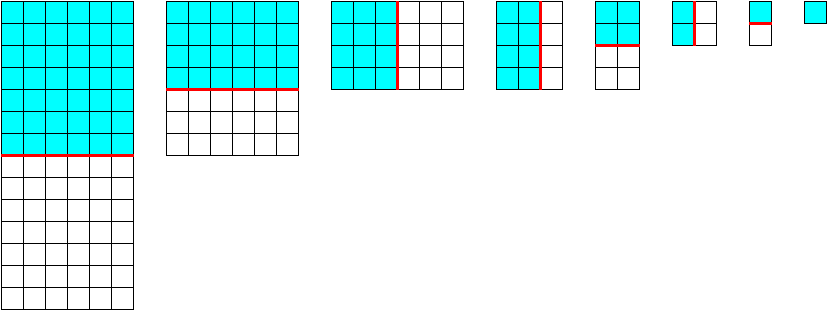
Folge von Quasi-Halbierungen
Wir bezeichnen mit "Quasi-Halbierung" die Abtrennung von [k/2] Reihen von insgesamt k Reihen, so wie im vorigen Bild (d.h. entweder [k/2] Zeilen oder [k/2] Spalten; [·] ist die Gaußklammer, in MATHEMATICA: Floor[·] ). Das abgetrennte Rechteck spielt für die weiteren Schnitte keine Rolle mehr, da es auf das andere (größere oder gleich große) gelegt werden darf. Es bedeutet keine Einschränkung, wenn man immer rechts oder unten wegschneidet, so dass bei jedem Schnitt die linke obere Ecke liegen bleibt. Jede Folge von Quasi-Halbierungen endet also beim linken oberen Quadrat.
Dass dieses Verfahren optimal ist, lässt sich einfach nachweisen: Bei einer waagerechten Teilung würde jeder andere Schnitt als die Quasi-Halbierung ein größeres Rechteck zurücklassen, also gleich viele oder mehr waagerechte Schnitte erfordern; gleiches gilt für eine senkrechte Teilung. Die Reihenfolge der Quasi-Halbierungen (waagerecht - senkrecht) ist unerheblich für die Anzahl der Schnitte, weil ein waagerechter Schnitt die Zahl der noch ungeschnittenen senkrechten Trennlinien unverändert lässt - und umgekehrt.
Wieviele Schnitte werden benötigt? Offenbar benötigt man für n = 2r Zeilen r waagerechte Schnitte - jeder dieser Schnitte ist eine exakte Halbierung (analoges gilt für die Spalten). Aber für 2r-1 < n < 2r kommt man auch nicht mit weniger Schnitten aus, denn bei r-1 Quasi-Halbierungen bleiben mindestens n/2r-1 Zeilen übrig, und n/2r-1 > 1 .
Das kann man so ausdrücken: Ist n eine Zweierpotenz 2r , so werden r = log2n waagerechte Schnitte benötigt. Ansonsten wählt man die nächsthöhere Zweierpotenz über n und nimmt den Exponenten für die Anzahl der Schnitte. Genauso geht man bei den m Spalten vor. Addiert man die minimale Anzahl der waagerechten und der senkrechten Schnitte, erhält man für die minimale Schnittanzahl s ( <·> steht für die Aufrundung auf die nächsthöhere natürliche Zahl, in MATHEMATICA: Ceiling[·] ) :
|
s = < log2 n > + < log2 m >
|
Publiziert 2008-01-18 Stand 2007-09-03
voriges Problem | Liste aller Probleme mit Lösungen | nächstes Problem
Manfred Börgens |
zur Leitseite
 English version
English version

