English version
Parabel im Quadrat

f  sei ein quadratisches Polynom der Form  f(x) = x² + b^.x + c  mit  b,c ∈ R .

Für welche  b,c  gilt  f: [-1,1] → [-1,1] ?

Gesucht sind also diejenigen Parabeln  f(x) = x² + b^.x + c ,  deren Graph für  x ∈ [-1,1]  vollständig im Quadrat  [-1,1]²  liegt.

Lösung

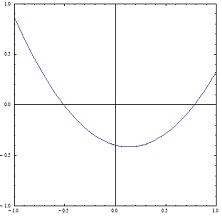
Man erkennt schnell, dass  |b| ≤ 1  und  |c| ≤ 1  gelten muss:  Aus  f(0)= c  folgt  |c| ≤ 1 ;  aus  f(-1)= 1 - b + c ∈ [-1,1]  und  f(1)= 1 + b + c ∈ [-1,1]  folgt  2b = f(1)-f(-1)∈ [-2,2] .

Hier geht es um Parabeln, die sich nach oben öffnen, also ein striktes absolutes Minimum haben. Deshalb sind nur zwei Bedingungen zu überprüfen:

a)  Die beiden Randpunkte müssen in  [-1,1]  liegen, es müssen also  b  und  c  gefunden werden, für die  f(-1)∈ [-1,1]  und  f(1)∈ [-1,1]  gilt.

b)  Wir werden ohne Mühe feststellen, dass das Minimum der Parabel bei  x = x_extr ∈ [-1/2, 1/2]  angenommen wird; dort gilt  f'(x_extr) = 0 .  Die zweite Bedingung lautet also:  f(x_extr) ∈ [-1,1] .

Zu a)

a) ist teilweise schon im ersten Abschnitt untersucht worden, aber dort steht nur die Richtung
f(-1)∈ [-1,1]  und  f(1)∈ [-1,1]  ⇒ ... ,  aber keine Äquivalenz.

Um zu einer Äquivalenz zu gelangen, gehen wir in vier Schritten vor:

(1)   f(1) ≤ 1  ⇔  1 + b + c ≤ 1  ⇔  c ≤ -b

(2)   f(1) ≥ -1  ⇔  1 + b + c ≥ -1 .  Dies ist wegen  b ≥ -1  und  c ≥ -1  immer erfüllt.

(3)   f(-1) ≤ 1  ⇔  1 - b + c ≤ 1  ⇔  c ≤ b

(4)   f(-1) ≥ -1  ⇔  1 - b + c ≥ -1 .  Dies ist wegen  b ≤ 1  und  c ≥ -1  immer erfüllt.

(1) - (4) lassen sich zusammenfassen als

(5)   c ≤ -|b| .  Insbesondere muss  c ≤ 0  gelten.



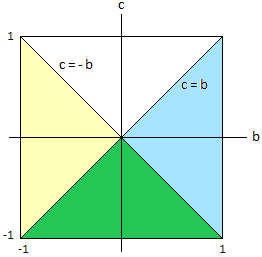
Bild 1

Die blau-grüne Fläche in Bild 1 steht für  c ≤ b ,  die gelb-grüne Fläche für  c ≤ -b .  Die grüne Fläche ist die Schnittmenge und enthält die Paare (b,c) mit  c ≤ -|b| ;  genau für diese liegen die Randpunkte der Parabel in  [-1,1] .

Zu b)

Innerhalb der grünen Fläche in Bild 1 müssen jetzt noch diejenigen Punkte (b,c) bestimmt werden, für die das Minimum des Graphen in  [-1,1]  liegt.

Man stellt zunächst fest, dass das absolute Minimum der Parabel für ein  x = x_extr ∈ [-1/2, 1/2]  angenommen wird:

f'(x) = 2x + b = 0  ⇔  x = -b/2

Also ist  x_extr = -b/2 ∈ [-1/2, 1/2]  und  f(x_extr) = -b²/4 + c ≤ 0 .  Der Tiefpunkt der Parabel liegt insbesondere immer in der unteren Halbebene.

In der grünen Fläche in Bild 1 erfüllen genau die Paare (b,c) mit  -b²/4 + c ∈ [-1,0] ,  also  b²/4 - 1 ≤ c ≤ b²/4  die Bedingung, dass  f(x_extr) ∈ [-1,1] .  c ≤ b²/4  ist aber wegen  c ≤ 0  trivialerweise erfüllt, so dass die Bedingung lediglich lautet:

(6)   c ≥ b²/4 - 1 

Für welche  b  ist (6) möglich? Man kann hier schon einmal Bild 2 anschauen; dort ist der Graph von  c = b²/4 - 1  als unterer Rand der grünen Fläche eingezeichnet. Dieser Graph reicht offenbar nicht bis  b = 1  oder  b = -1 ,  denn nach (5) gilt die Einschränkung  c ≤ -|b| (grüne Fläche in Bild 1). Wir suchen deshalb die Schnittpunkte von  c = b²/4 - 1  und  c = -|b| .  Für den rechten Schnittpunkt, also für  b > 0 ,  erhält man  b²/4 - 1 = -b  ⇔  b = √8 - 2 .  Aus Gründen der Symmetrie muss also gelten:

(7)   |b| ≤ 2(√2 - 1) ≈ 0,8284


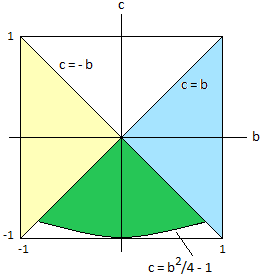
Bild 2

Wir fassen (5), (6) und (7) zusammen:

|b| ≤ 2(√2 - 1)     c ∈ [b²/4 - 1, -|b|]

Diese Paare (b,c) werden durch die grüne Fläche in Bild 2 dargestellt.


Beispiel:  Für  b = 1/2  kommen alle  c ∈ [-15/16, -1/2]  in Frage, also z.B. die Parabel  f(x) = x² + x/2 - 3/4 , die man in Bild 3 sieht.



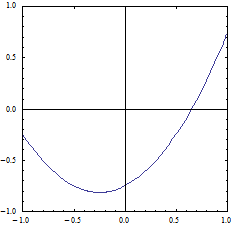
Bild 3


Ein ähnliches Problem erschien in Mathematical Excalibur 1/2, Problem 6.

Publiziert 2019-03-25          Stand 2018-03-01

voriges Problem   |   Liste aller Probleme mit Lösungen   |    nächstes Problem