Manfred Boergens

MB Matheblog # 31

2024-01-10

Strings of beads Comments are welcome

We want to determine the number \(a(n,m)\) of strings of \(n\) beads with colours chosen from \(m\) colours.

There are three binary characteristics which allow a discrimination of the strings:
– open / closed
– oriented / reversible
– exactly \(m\) colours / \(1~...~\text{min}(n,m)\) colours chosen from \(m\) colours

With these characteristics we get eight types of strings. In order to define \(a(n,m)\) for the different types we write \(a...(n,m)\) and insert abbreviations of the characteristics in the dots.

Figure 1 shows two open strings (left) and two closed strings (right). Closed chains are considered identical if they coincide after a suitable rotation.

In the reversible case mirror images of strings are considered identical, otherwise the strings are oriented. The open strings in figure 1 (left) resp. the closed strings (right) count as different in the oriented case and as identical in the reversible case.

open vs. closed

Figure 1 \(n~=~4~~~~m\ge~3\) left: open strings right: closed strings

Below all eight types of strings will be analysed. For each \(a...(n,m)\) we give a link to the corresponding sequence in the OEIS.

The proofs of the formulae for the open strings are quite easy: 2. is trivial; 1. results from 2.; 4. will be worked out; 3. results from 4.

The proofs make use of the Stirling numbers of the second kind \(S_2(a,b)\) and the binomial inversion formula (*): \[S_2(a,b)~=~\frac{1}{b~!}~\sum_{j=0}^b~(-1)^{b+j}~\binom{b}{j}~j^{~a}\] \[\text{(*)}~~~a_m = \sum_{j=0}^m \binom{m}{j}~b_j~~~~\Rightarrow~~~~b_m = \sum_{j=0}^m~(-1)^{m-j}~\binom{m}{j}~a_j\]

1. Open oriented strings with exactly \(m\) colours

OEIS A019538 \[a_{~\text{open, ori, ex}~}(n,m)~=~(-1)^m~\sum_{j=1}^m (-1)^j~\binom{m}{j}~j^n~=~m!~S_2(n,m)\] The formulae are given in the OEIS. The first formula is proved by observing that the number of open oriented strings with colours chosen from \(m\) colours is \(m^n\) (see 2.) . By applying the binomial inversion formula (*) to the second formula in 2. the proof is completed.

The following table shows the \(a...(n,m)\) for \(m~=~1~...~n\) in the \(n^{th}\) row.

1 1 2 1 6 6 1 14 36 24 1 30 150 240 120

\(a_{~\text{open, ori, ex}~}(n,m)\) also gives the number of disjunct coverings of sets by non-empty subsets, see Comments in A019538.

2. Open oriented strings with \(1~...~\text{min}(n,m)\) colours chosen from \(m\) colours

OEIS A051129 \[a_{~\text{open, ori, max}~}(n,m)~=~m^n\] \[a_{~\text{open, ori, max}~}(n,m)~=~\sum_{i=1}^{min~(m,~n)} \binom{m}{i}~a_{~\text{off, ori, ex}~}(n,i)~~~~~~\text{see 1.}\] The following table shows the \(a...(n,m)\) for \(m~=~1,~2,~...\) in the \(n^{th}\) row.

1 2 3 4 5 6 1 4 9 16 25 36 1 8 27 64 125 216 1 16 81 256 625 1296 1 32 243 1024 3125 7776

3. Open reversible strings with exactly \(m\) colours

OEIS A305621 \[a_{~\text{open, rev, ex}~}(n,m)~=~\frac{m!}{2}~(S_2(n,m)+S_2(\left\lceil n/2 \right\rceil,m)~=~\frac{(-1)^m}{2}~\sum_{j=1}^m (-1)^j~\binom{m}{j}~(j^n+j^{ \left\lceil n/2 \right\rceil})\] The first formula is given in the OEIS. The second formula is derived from the first; it can be proved by applying the binomial inversion formula (*) to the second formula in 4.

The following table shows the \(a...(n,m)\) for \(m~=~1~...~n\) in the \(n^{th}\) row.

1 1 1 1 4 3 1 8 18 12 1 18 78 120 60

4. Open reversible strings with \(1~...~\text{min}(n,m)\) colours chosen from \(m\) colours

OEIS A277504

In OEIS we read " \(n\) beads of \(k\) or fewer colors " (OEIS uses \(k\) instead of \(m\)). This could lead to the erroneous interpretation that we are looking for the total number of all one-coloured, two-coloured ... \(m\)-coloured strings. The correct interpretation is: For an \(i\)-coloured string the \(i\) colours are chosen from \(m\) colours (see the second formula below). \[a_{~\text{open, rev, max}~}(n,m)~=~\frac{1}{2}~(m^n+m^{ \left\lceil n/2 \right\rceil})\] \[a_{~\text{open, rev, max}~}(n,m)~=~\sum_{i=1}^{min~(m,~n)} \binom{m}{i}~a_{~\text{off, rev, ex}~}(n,i)~~~~~~\text{see 3.}\] The first formula is given in the OEIS. The proof starts with counting the symmetric strings in which the left \(\left\lceil n/2 \right\rceil\) beads can each be coloured with one from \(m\) colours; the colours of the other beads are determined. We get \(m^{\left\lceil n/2 \right\rceil}\) symmetric strings, leaving \(m^n - m^{\left\lceil n/2 \right\rceil}\) asymmetric strings. The reversibility only applies to the asymmetric strings; their number must be halved. Thus we get \[a...(n,m) = m^{\left\lceil n/2 \right\rceil} + \frac{1}{2}(m^n - m^{\left\lceil n/2 \right\rceil})~=~\frac{1}{2}~(m^n+m^{ \left\lceil n/2 \right\rceil})\] The following table shows the \(a...(n,m)\) for \(m~=~1,~2,~...\) in the \(n^{th}\) row.

1 2 3 4 5 6 1 3 6 10 15 21 1 6 18 40 75 126 1 10 45 136 325 666 1 20 135 544 1625 3996

Figure 2 shows an example: There are \(6\) different open reversible strings with \(2\) beads and colours chosen from \(3\) colours.

4. a(2,3)

Figure 2 \(a_{~\text{open, rev, max}~}(2,3)~=~6\)

Remark to closed strings

In OEIS and Mathematica the notation for closed strings is confusing. In OEIS necklaces are oriented (although they could be turned around) and bracelets are reversible. The use of necklaces in Mathematica is different as the next table shows.

	OEIS and Wikipedia	Mathematica and MathWorld
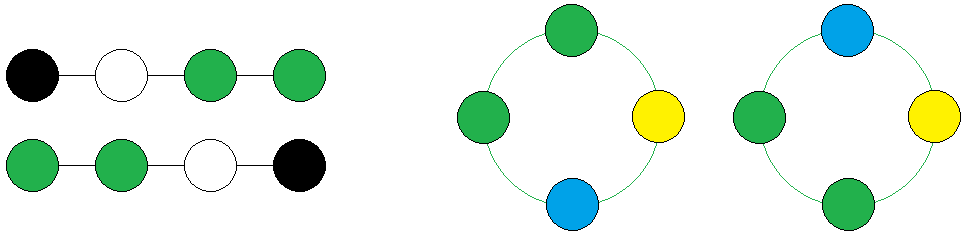
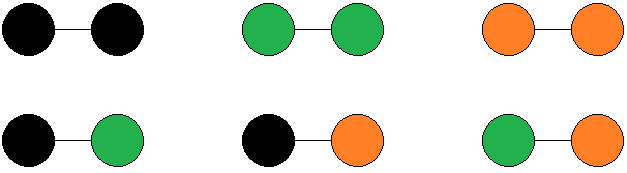
closed, oriented, exactly m	necklaces A087854
closed, oriented, max. m	necklaces A075195	necklaces Cyclic
closed, reversible, exactly m	bracelets A273891
closed, reversible, max. m	bracelets A321791	necklaces Dihedral

\(\phi(N)\) is Euler's totient function giving the number of positive integers \(\le N\) that are relatively prime to \(N\) .

5. Closed oriented strings with exactly \(m\) colours

OEIS A087854 \[a_{~\text{closed, ori, ex}~}(n,m)~=~\frac{m!}{n}~\sum_{d|n} \phi\left(\frac{n}{d}\right)~S_2(d,m)\] The formula is given in the OEIS and in Wikipedia.

The following table shows the \(a...(n,m)\) for \(m~=~1~...~n\) in the \(n^{th}\) row.

1 1 1 1 2 2 1 4 9 6 1 6 30 48 24

6. Closed oriented strings with \(1~...~\text{min}(n,m)\) colours chosen from \(m\) colours

OEIS A075195 \[a_{~\text{closed, ori, max}~}(n,m)~=~\frac{1}{n}~\sum_{d|n} \phi\left(\frac{n}{d}\right)~m^d~=~\frac{1}{n}~\sum_{j=1}^n m^{ggt~(j,n)}\] \[a_{~\text{closed, ori, max}~}(n,m)~=~\sum_{i=1}^{min~(m,~n)} \binom{m}{i}~a_{~\text{closed, ori, ex}~}(n,i)~~~~~~\text{see 5.}\] The formulae in the upper line are given in the OEIS, in Wikipedia and in MathWorld.

The following table shows the \(a...(n,m)\) for \(m~=~1,~2,~...\) in the \(n^{th}\) row.

1 2 3 4 5 6 1 3 6 10 15 21 1 4 11 24 45 76 1 6 24 70 165 336 1 8 51 208 629 1560

7. Closed reversible strings with exactly \(m\) colours

OEIS A273891 \[a_{~\text{closed, rev, ex}~}(n,m)~=~\frac{m!}{4}~\left(S_2\left(\left\lfloor \frac{n+1}{2} \right\rfloor,m\right)+S_2\left(\left\lceil \frac{n+1}{2} \right\rceil,m\right)\right)+\frac{m!}{2n}~\sum_{d|n} \phi\left(\frac{n}{d}\right)~S_2(d,m)\] The formula is given in the OEIS.

The following table shows the \(a...(n,m)\) for \(m~=~1~...~n\) in the \(n^{th}\) row.

1 1 1 1 2 1 1 4 6 3 1 6 18 24 12

Figure 3 shows an example: There are \(6\) different closed reversible strings with \(4\) beads and exactly \(3\) colours.

7. a(4,3)

Figure 3 \(a_{~\text{closed, rev, ex}~}(4,3)~=~6\)

8. Closed reversible strings with \(1~...~\text{min}(n,m)\) colours chosen from \(m\) colours

OEIS A321791 \[a_{~\text{closed, rev, max}~}(n,m)~=~\left(m^{\left\lfloor\frac{n+1}{2}\right\rfloor}+m^{\left\lceil\frac{n+1}{2}\right\rceil}\right)/4~+~\frac{1}{2n}\sum_{d|n} \phi\left(\frac{n}{d}\right)~m^d~=~\left(m^{\left\lfloor\frac{n+1}{2}\right\rfloor}+m^{\left\lceil\frac{n+1}{2}\right\rceil}\right)/4~+~\frac{1}{2n}\sum_{j=1}^n m^{gcd~(j,n)}\] \[a_{~\text{closed, rev, max}~}(n,m)~=~\sum_{i=1}^{min~(m,~n)} \binom{m}{i}~a_{~\text{closed, rev, ex}~}(n,i)~~~~~~\text{see 7.}\] The first formula is given in the OEIS; for other (longer) formulas see Wikipedia and MathWorld.

The following table shows the \(a...(n,m)\) for \(m~=~1,~2,~...\) in the \(n^{th}\) row.

1 2 3 4 5 6 1 3 6 10 15 21 1 4 10 20 35 56 1 6 21 55 120 231 1 8 39 136 377 888

Last update 2024-01-09

blog overview | previous article

Manfred Börgens | main page