Manfred Boergens

MB Matheblog # 31

Inhalt Blog
voriger Eintrag nächster Eintrag

zur Leitseite
Index der gesamten Website

2024-01-09

Perlenketten Kommentare sind willkommen.

Es soll die Anzahl \(a(n,m)\) der möglichen Perlenketten mit \(n\) Perlen, deren Farben aus \(m\) Farben gewählt werden, berechnet werden.

Für die Ketten gibt es drei Unterscheidungsmerkmale:
– offen / geschlossen
– orientiert / reversibel
– genau \(m\) Farben / \(1~...~\text{min}(n,m)\) Farben aus \(m\) Farben ausgewählt

Es treten also acht Typen von Ketten auf. Zur Unterscheidung der jeweiligen \(a(n,m)\) schreiben wir \(a...(n,m)\) und setzen für die Pünktchen Abkürzungen für die Merkmale ein.

In Bild 1 sehen wir links zwei offene Ketten, rechts zwei geschlossene Ketten. Bei geschlossenen Ketten werden Ketten als identisch angesehen, die durch Rotation in Deckung gebracht werden können.

Bei der Zählung reversibler Ketten sind Spiegelungen erlaubt, bei orientierten nicht. Die offenen Ketten in Bild 1 links bzw. die geschlossenen Ketten in Bild 1 rechts zählen also im orientierten Fall als verschieden und im reversiblen Fall als identisch.

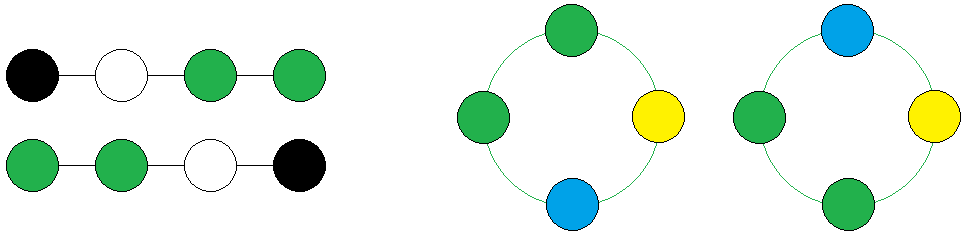
offen vs. geschlossen

Bild 1 \(n~=~4~~~~m\ge~3\) links: offene Ketten rechts: geschlossene Ketten

Im Folgenden werden alle acht Kettentypen behandelt. Zu \(a...(n,m)\) wird jeweils ein Link zu der zugehörigen Folge in der Datenbank OEIS gegeben.

Für die offenen Ketten sind die Formeln leicht beweisbar: 2. ist trivial; 1. folgt aus 2.; 4. wird ausgeführt; 3. folgt aus 4.

Für die Beweise benötigen wir die Stirling-Zahlen 2. Art \(S_2(a,b)\) und die Binomische Inversionsformel (*): \[S_2(a,b)~=~\frac{1}{b~!}~\sum_{j=0}^b~(-1)^{b+j}~\binom{b}{j}~j^{~a}\] \[\text{(*)}~~~a_m = \sum_{j=0}^m \binom{m}{j}~b_j~~~~\Rightarrow~~~~b_m = \sum_{j=0}^m~(-1)^{m-j}~\binom{m}{j}~a_j\]

1. Offene orientierte Ketten mit genau \(m\) Farben

OEIS A019538 \[a_{~\text{off, ori, ex}~}(n,m)~=~(-1)^m~\sum_{j=1}^m (-1)^j~\binom{m}{j}~j^n~=~m!~S_2(n,m)\] Die Formel stammt aus OEIS. Zum Beweis nimmt man die Anzahl \(m^n\) für Ketten mit \(1~...~m\) aus \(m\) Farben (siehe 2.) und wendet dann die binomische Inversionsformel (*) auf die zweite Formel in 2. an.

In der folgenden Tabelle stehen die \(a...(n,m)\) für \(m~=~1~...~n\) in der \(n-\)ten Zeile.

1 1 2 1 6 6 1 14 36 24 1 30 150 240 120

\(a...(n,m)\) findet man auch bei der Berechnung der Anzahl von disjunkten Überdeckungen von Mengen durch nicht-leere Teilmengen, siehe Blog # 10 und Comments in A019538.

2. Offene orientierte Ketten mit \(1~...~\text{min}(n,m)\) Farben aus \(m\) Farben ausgewählt

OEIS A051129 \[a_{~\text{off, ori, max}~}(n,m)~=~m^n\] \[a_{~\text{off, ori, max}~}(n,m)~=~\sum_{i=1}^{min~(m,~n)} \binom{m}{i}~a_{~\text{off, ori, ex}~}(n,i)~~~~~~\text{siehe 1.}\] In der folgenden Tabelle stehen die \(a...(n,m)\) für \(m~=~1,~2,~...\) in der \(n-\)ten Zeile.

1 2 3 4 5 6 1 4 9 16 25 36 1 8 27 64 125 216 1 16 81 256 625 1296 1 32 243 1024 3125 7776

3. Offene reversible Ketten mit genau \(m\) Farben

OEIS A305621 \[a_{~\text{off, rev, ex}~}(n,m)~=~\frac{m!}{2}~(S_2(n,m)+S_2(\left\lceil n/2 \right\rceil,m)~=~\frac{(-1)^m}{2}~\sum_{j=1}^m (-1)^j~\binom{m}{j}~(j^n+j^{ \left\lceil n/2 \right\rceil})\] Die erste Formel stammt aus OEIS. Die zweite Formel ist nur eine leichte Umformulierung aus der ersten; sie wird bewiesen mit der binomischen Inversionsformel (*), angewendet auf die zweite Formel in 4.

In der folgenden Tabelle stehen die \(a...(n,m)\) für \(m~=~1~...~n\) in der \(n-\)ten Zeile.

1 1 1 1 4 3 1 8 18 12 1 18 78 120 60

4. Offene reversible Ketten mit \(1~...~\text{min}(n,m)\) Farben aus \(m\) Farben ausgewählt

OEIS A277504

In OEIS ist die Formulierung " \(n\) beads of \(k\) or fewer colors " (OEIS verwendet \(k\) statt \(m\)) missverständlich. Es könnte der Eindruck entstehen, dass es hier um die Gesamtzahl aller einfarbigen, zweifarbigen, ... , \(m-\)farbigen Ketten geht. Die korrekte Interpretation ist: Bei einer \(i-\)farbigen Kette werden die \(i\) Farben aus \(m\) Farben ausgewählt, so wie unten in der zweiten Formel. \[a_{~\text{off, rev, max}~}(n,m)~=~\frac{1}{2}~(m^n+m^{ \left\lceil n/2 \right\rceil})\] \[a_{~\text{off, rev, max}~}(n,m)~=~\sum_{i=1}^{min~(m,~n)} \binom{m}{i}~a_{~\text{off, rev, ex}~}(n,i)~~~~~~\text{siehe 3.}\] Die erste Formel stammt aus OEIS. Zum Beweis zählt man zunächst alle symmetrischen Ketten. Bei diesen können die linken \(\left\lceil n/2 \right\rceil\) Perlen jeweils mit einer aus \(m\) Farben belegt werden; die anderen Perlen sind dann festgelegt. Somit gibt es \(m^{\left\lceil n/2 \right\rceil}\) symmetrische Ketten. Es verbleiben \(m^n - m^{\left\lceil n/2 \right\rceil}\) asymmetrische Ketten; nur für diese greift die Reversibilität, so dass die Anzahl halbiert werden muss. Insgesamt ist also \[a...(n,m) = m^{\left\lceil n/2 \right\rceil} + \frac{1}{2}(m^n - m^{\left\lceil n/2 \right\rceil})~=~\frac{1}{2}~(m^n+m^{ \left\lceil n/2 \right\rceil})\] In der folgenden Tabelle stehen die \(a...(n,m)\) für \(m~=~1,~2,~...\) in der \(n-\)ten Zeile.

1 2 3 4 5 6 1 3 6 10 15 21 1 6 18 40 75 126 1 10 45 136 325 666 1 20 135 544 1625 3996

Bild 2 zeigt ein Beispiel: Es gibt \(6\) verschiedene offene reversible Ketten mit \(2\) Perlen und mit Farben, die aus \(3\) Farben ausgewählt werden.

4. a(2,3)

Bild 2 \(a_{~\text{off, rev, max}~}(2,3)~=~6\)

Vorbemerkung zu geschlossenen Ketten

In OEIS und Mathematica sind die englischen Bezeichnungen verwirrend. Insbesondere erscheint es merkwürdig, dass in OEIS necklaces (Halsketten) immer orientiert sind (obwohl man Halsketten natürlich auch umdrehen kann). Zur Unterscheidung sind dann bracelets (Armreife) immer reversibel. Mathematica verwendet necklaces anders, siehe folgende Tabelle.

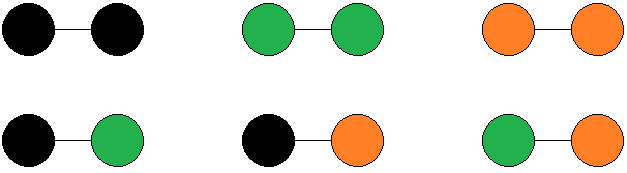
	OEIS und Wikipedia (engl.)	Mathematica und MathWorld
geschlossen, orientiert, genau m	necklaces (Halsketten) A087854
geschlossen, orientiert, max. m	necklaces (Halsketten) A075195	necklaces (Halsketten) Cyclic
geschlossen, reversibel, genau m	bracelets (Armreife) A273891
geschlossen, reversibel, max. m	bracelets (Armreife) A321791	necklaces (Halsketten) Dihedral

Im Folgenden ist \(\phi(N)\) die Eulersche \(\phi-\)Funktion für die Anzahl der zu \(N\) teilerfremden positiven natürlichen Zahlen \(\le N\) .

5. Geschlossene orientierte Ketten mit genau \(m\) Farben

OEIS A087854 \[a_{~\text{geschl, ori, ex}~}(n,m)~=~\frac{m!}{n}~\sum_{d|n} \phi\left(\frac{n}{d}\right)~S_2(d,m)\] Die Formel stammt aus OEIS und aus Wikipedia.

In der folgenden Tabelle stehen die \(a...(n,m)\) für \(m~=~1~...~n\) in der \(n-\)ten Zeile.

1 1 1 1 2 2 1 4 9 6 1 6 30 48 24

6. Geschlossene orientierte Ketten mit \(1~...~\text{min}(n,m)\) Farben aus \(m\) Farben ausgewählt

OEIS A075195 \[a_{~\text{geschl, ori, max}~}(n,m)~=~\frac{1}{n}~\sum_{d|n} \phi\left(\frac{n}{d}\right)~m^d~=~\frac{1}{n}~\sum_{j=1}^n m^{ggt~(j,n)}\] \[a_{~\text{geschl, ori, max}~}(n,m)~=~\sum_{i=1}^{min~(m,~n)} \binom{m}{i}~a_{~\text{geschl, ori, ex}~}(n,i)~~~~~~\text{siehe 5.}\] Die obere Formelzeile stammt aus OEIS, Wikipedia und MathWorld.

In der folgenden Tabelle stehen die \(a...(n,m)\) für \(m~=~1,~2,~...\) in der \(n-\)ten Zeile.

1 2 3 4 5 6 1 3 6 10 15 21 1 4 11 24 45 76 1 6 24 70 165 336 1 8 51 208 629 1560

7. Geschlossene reversible Ketten mit genau \(m\) Farben

OEIS A273891 \[a_{~\text{geschl, rev, ex}~}(n,m)~=~\frac{m!}{4}~\left(S_2\left(\left\lfloor \frac{n+1}{2} \right\rfloor,m\right)+S_2\left(\left\lceil \frac{n+1}{2} \right\rceil,m\right)\right)+\frac{m!}{2n}~\sum_{d|n} \phi\left(\frac{n}{d}\right)~S_2(d,m)\] Die Formel stammt aus OEIS.

In der folgenden Tabelle stehen die \(a...(n,m)\) für \(m~=~1~...~n\) in der \(n-\)ten Zeile.

1 1 1 1 2 1 1 4 6 3 1 6 18 24 12

Bild 3 zeigt ein Beispiel:: Es gibt \(6\) verschiedene geschlossene reversible Ketten mit \(4\) Perlen und genau \(3\) Farben.

7. a(4,3)

Bild 3 \(a_{~\text{geschl, rev, ex}~}(4,3)~=~6\)

8. Geschlossene reversible Ketten mit \(1~...~\text{min}(n,m)\) Farben aus \(m\) Farben ausgewählt

OEIS A321791 \[a_{~\text{geschl, rev, max}~}(n,m)~=~\left(m^{\left\lfloor\frac{n+1}{2}\right\rfloor}+m^{\left\lceil\frac{n+1}{2}\right\rceil}\right)/4~+~\frac{1}{2n}\sum_{d|n} \phi\left(\frac{n}{d}\right)~m^d~=~\left(m^{\left\lfloor\frac{n+1}{2}\right\rfloor}+m^{\left\lceil\frac{n+1}{2}\right\rceil}\right)/4~+~\frac{1}{2n}\sum_{j=1}^n m^{ggt~(j,n)}\] \[a_{~\text{geschl, rev, max}~}(n,m)~=~\sum_{i=1}^{min~(m,~n)} \binom{m}{i}~a_{~\text{geschl, rev, ex}~}(n,i)~~~~~~\text{siehe 7.}\] Die obere Formelzeile stammt aus OEIS, siehe auch umständlichere Formeln in Wikipedia und MathWorld.

In der folgenden Tabelle stehen die \(a...(n,m)\) für \(m~=~1,~2,~...\) in der \(n-\)ten Zeile.

1 2 3 4 5 6 1 3 6 10 15 21 1 4 10 20 35 56 1 6 21 55 120 231 1 8 39 136 377 888

Stand 2024-01-09

Inhalt Blog | voriger Eintrag | nächster Eintrag

Manfred Börgens | Zur Leitseite