Dodekaeder    MB Matheblog # 28 blog overview
previous article    next article		 main page
index website

2023-08-14 deutsche Flagge  deutsche Version


North - East - South - West                    Comments are welcome


In an old and well-known problem a wanderer goes \(~1~\text{Mile}~\) south, then \(~1~\text{Mile}~\) east, then \(~1~\text{Mile}~\) north and arrives at her starting point  –  where did she start? You will find it in many books and the Internet. Reportedly Microsoft and Elon Musk have confronted job candidates with this problem. If you happen to be not familiar with it you can read about it on the commendable Website by book author and YouTuber Presh Talwalkar, in the 2011-02-22 blog post. The problem is a classic one. Most solvers find a solution within minutes. The contentment with their achievement often inhibits the insight that there are many more solutions which do not suggest themselves so easyly, and even when this dawns on the solvers they sometimes get no general view over the multitude of solutions. So this old problem has its appeal, and in this blog post we discuss a quite similar one which leads to a gradually increasing intricacy in finding the various sets of solutions. It is mathematically much more challenging and interesting than the old problem.

This is the problem:

A drone flies \(~100~\text{km}~\) north, then \(~100~\text{km}~\) east, then \(~100~\text{km}~\) south, then \(~100~\text{km}~\) west and arrives at its starting position. On which circle of latitude did the drone start?

We want to generalize the question to other stages than \(~100~\text{km}~\).  Do there exist solutions for all stages less than half of the circumference of the Earth?

Try to find a solution yourself  –  or even more than one!

A. Posamentier and W. Schulz discuss this problem in their book  The Art of Problem Solving [1].  They do not present an own method of solution but refer to an older source from 1983, the problem itself being at least as old as from 1959. The authors stop short of giving a complete solution but give a sufficient starting point for a comprehensive completion of the solution by the problem solver.

The following box sets the frame and gives some definitions for the further mathematical dealing with the problem:

  • The Earth is considered as spherical with a circumference of \(~40030~\text{km}~\).

  • Latitudes are in the interval \(~[-90°,_~90°]~\),  longitudes in \(~[_~0°,_~360°)~\),  counted eastward.

  • The flight of the drone covers four stages:

    • 1st stage north along a meridian; for convenience we take the \(~0°-\)meridian; every other meridian would serve our purpose equally well.

    • 2nd stage east ("north stage") along a circle of latitude ("north circle").

    • 3rd stage south along a meridian.

    • 4th stage west ("south stage") along a circle of latitude ("south circle"); this circle is the same as the circle of latitude where the journey started  –  representing the solution to our problem.

    • The terms "north and south circle" do not refer to the north and south hemisphere !

    • The length of a stage is \(~s~\) and will be measured in \(~\text{km}~\).

  • North and south circle are given with their latitudes \(~\phi + d~\) and \(~\phi - d~\) with \(~d \in (0°,_~90°)\). \(~\phi~\) is the mean of the two latitudes. \(~\phi - d~\) is the solution of the problem.

    \(s~\) and \(~d~\) are easyly converted. \(~d~\) corresponds to half a stage along a meridian: \[d = (s/80060) \cdot 360°~~~~~~~~~s = (d/360°) \cdot 80060\] Our approach to a solution will only rely on \(~d~\); within examples \(~s~\) will be specified too. Taking \(~d~\) as input makes things easier because it is independent from the circumference of the sphere and can be converted to lengths on other spheres as the Earth.


North and south circles have the circumference \(~40030 \cdot \text{cos}_~(\phi \pm d)~\text{km}~\),  this correponds to an orthodromic distance of \(~360° \cdot \text{cos}_~(\phi \pm d)~\) measured as central angle (the vertex in the center of the Earth). On these circles the drone flies along a stage with "length" \(~2_~d~\).

One should be careful when identifying lengths and central angles on the sphere: The circumference of, say, the north circle as well as \(~d~\) are distances on the sphere the measures of which must be imagined as parts of great circles. This implies that \(~2_~d~\) given as a distance along a circle of latitude is not the interval length of the covered latitudes because this circle is not a great circle (with the exception of the equator).

The quotient \(~q = (2_~d)/(360° \cdot \text{cos}_~(\phi \pm d))~\) indicates how often the north or the south circle will be orbited. The longitudes along these circles have values in \(~[_~0°,_~360°)~\),  so \(~q \cdot 360°~\) tells how many longitudes are covered by one stage. This leads to the start of our solution in (1) und (2):

\[\textbf{(1)}~~~\text{Longitudes covered by the north stage:}~~\frac{2_~d}{\text{cos}~(\phi + d)}\] \[~~~~~~~~~~~~~~~\text{Longitude marking the end of the north stage:}~~~\lambda_1 = \frac{2_~d}{\text{cos}~(\phi + d)} - 2_~k_{1~} \pi\] \[~~~~~~~~~~~~~~~k_1~~\text{completed circuits going east}\]
\[\textbf{(2)}~~~\text{Longitudes covered by the south stage:}~~\frac{2_~d}{\text{cos}~(\phi - d)}\] \[~~~~~~~~~~~~~~~\text{Longitude marking the end of the south stage:}~~~\lambda_2 = \lambda_1 -\frac{2_~d}{\text{cos}~(\phi - d)} + 2_~k_{2~} \pi\] \[~~~~~~~~~~~~~~~k_2~~\text{completed circuits going west}\]
Getting back to the starting position after all four stages requires \(~\lambda_2 = 0_~\): \[\textbf{(3)}~~~\lambda_2 = 0~~~~\Rightarrow~~~~\frac{1}{\text{cos}~(\phi + d)} - \frac{1}{\text{cos}~(\phi - d)} = \frac{k_~\pi}{d}~~~~\text{with}~~~~k = k_1-k_2\] With this we get: \[\textbf{(4)}~~~\frac{k_~\pi}{d} = \frac{\text{cos}~(\phi - d) - \text{cos}~(\phi + d)}{\text{cos}~(\phi + d) \cdot \text{cos}~(\phi - d)} = 4 \cdot \frac{\text{sin}~\phi \cdot \text{sin}~d}{\text{cos}~2_~\phi~+~\text{cos}~2_~d} = 2 \cdot \frac{\text{sin}~\phi \cdot \text{sin}~d}{\text{cos}^2~d~-~\text{sin}^2~\phi}\]
First solution  ("equator solution") :  \(~k=0\)

(4) gives \(~\phi = 0~\).  The drone starts south of the equator on latitude \(~-d_~\).

\(k = 0~\) means \(~k_1 = k_2~\). The drone performs an equal number of complete circuits on north and south stages.
Example 1:  Stage length \(~800~\text{km}_~\).

\(~d~\approx~3,5973°~~\widehat{=}~~400~\text{km}\)

Once again: the degree-measurement is valid for a great circle, in our setting for the first and the third stage. It does not refer to the longitudes along the north and the south stage.

Along the north and the south circle  –  going east resp. west  – \(~2_~d/\text{cos}~(\pm d)~\approx~7,2088°\) (longitude) is covered, with \(~k_1 = k_2=0~\).
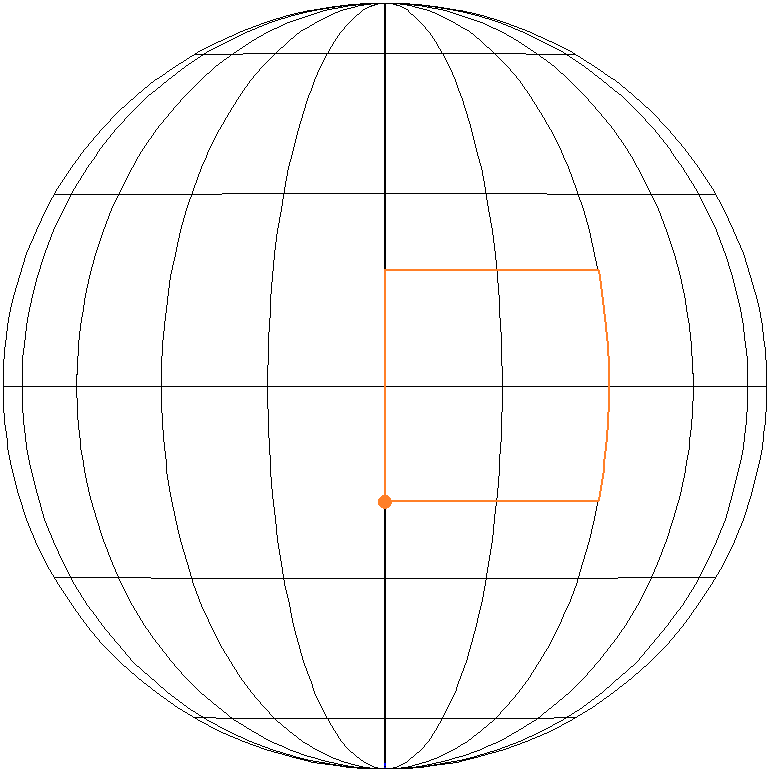
Example 2:  Stage length \(~18000~\text{km}_~\).

\(~d~\approx~80,9393°~~\widehat{=}~~9000~\text{km}\)

Along the north and the south circle \(~2_~d/\text{cos}~(\pm d)~\approx~1027,926°~=~2 \cdot 360°+307,926°\) (longitude) is covered, with \(~k_1 = k_2=2_~\).


Äquatorlösung

Figure 1  Equator solution with \(~k_i = 0~\);  the orange point is the starting point.


We proceed with (4) for \(~k \neq 0~\) and get the quadratic equation \[\text{sin}^2~\phi~+~\frac{2_~d}{k_~\pi}~\text{sin}~d~_~\text{sin}~\phi~-~\text{cos}^2~d~=~0\] \[\text{sin}~\phi~=~-\frac{d}{k_~\pi}~\text{sin}~d~\pm~\sqrt{\frac{d^{~2}}{k^2_~\pi^2}~\text{sin}^2~d~+~\text{cos}^2~d~}\] \[\textbf{(5)}~~~\phi~=~\text{arcsin}\left(-\frac{d}{k_~\pi}~\text{sin}~d~\pm~\sqrt{\frac{d^{~2}}{k^2_~\pi^2}~\text{sin}^2~d~+~\text{cos}^2~d~}\right)\]
Second solution  ("north solution") :  \(~k \gt 0\)

\(k_1 \gt k_2~\), hence the north circle sees more complete circuits by the drone than the south circle und is therefore the shorter one. This means \(~\phi \gt 0~\).  So in (5) only the "+"-solution has to be considered.
Example 3:  Stage length \(~2000~\text{km}_~\),  with \(~k=2_~\).

\(~d~\approx~8,9933°~~\widehat{=}~~1000~\text{km}\)

\(\phi~\approx~79,6758°\)

The drone starts on latitude \(70,6825°\).

First stage, going north, to latitude \(~88,6691°\).

Second stage (north stage) to the east covering \(~2_~d/\text{cos}~(\phi + d)~\approx~774,372°~=~2 \cdot 360°+54,372°\) (longitude) with \(~k_1 = 2~\).

Third stage, going south, to latitude \(70,6825°\).

Fourth stage (south stage) to the west covering \(~2_~d/\text{cos}~(\phi - d)~\approx~54,372°\) (longitude) with \(~k_2 = 0~\).
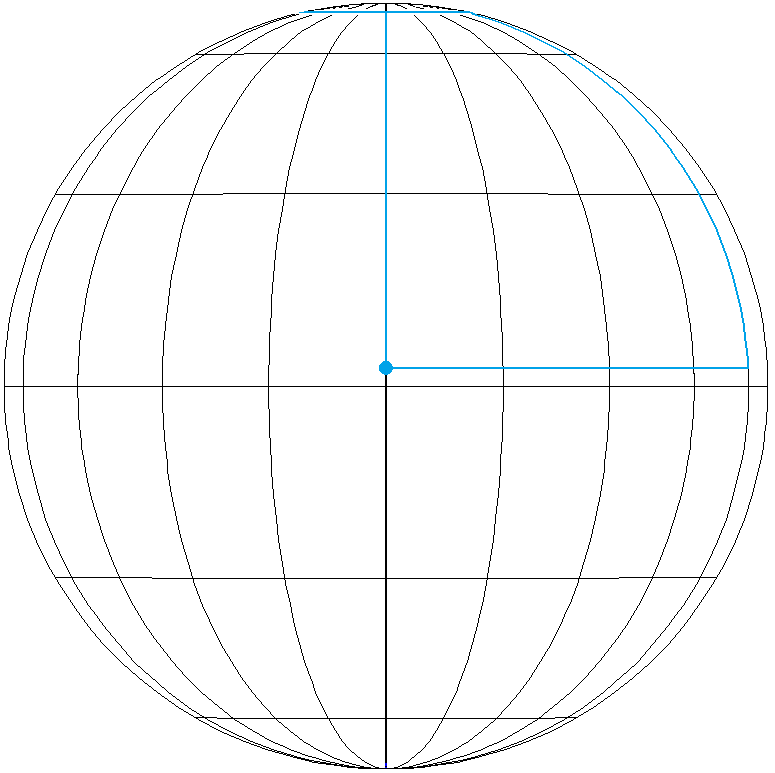
Example 4:  Stage length \(~16250~\text{km}_~\),  with \(~k=1_~\).

\(~d~\approx~73,0702°~~\widehat{=}~~8125~\text{km}\)

\(\phi~\approx~5,5693°\)

The drone starts on latitude \(-67,5009°\).

First stage, going north, to latitude \(78,6395°\).

Second stage (north stage) to the east covering \(~2_~d/\text{cos}~(\phi + d)~\approx~741,898°~=~2 \cdot 360°+21,898°\) (longitude) with \(~k_1 = 2~\).

Third stage, going south, to latitude \(-67,5009°\).

Fourth stage (south stage) to the west covering \(~2_~d/\text{cos}~(\phi - d)~\approx~381,898°~=~360°~+~21,898°\) (longitude) with \(~k_2 = 1~\).


Nordlösung

Figure 2  North solution with \(~k_2 = 0~\);  the blue point is the starting point.


Third solution  ("south solution") :  \(~k \lt 0\)

\(k_1 \lt k_2~\), hence the sourth circle sees more complete circuits by the drone than the north circle und is therefore the shorter one. This means \(~\phi \lt 0~\).  So in (5) only the "–"-solution has to be considered.  —  The second and the third solution are located symmetrically to the equator.
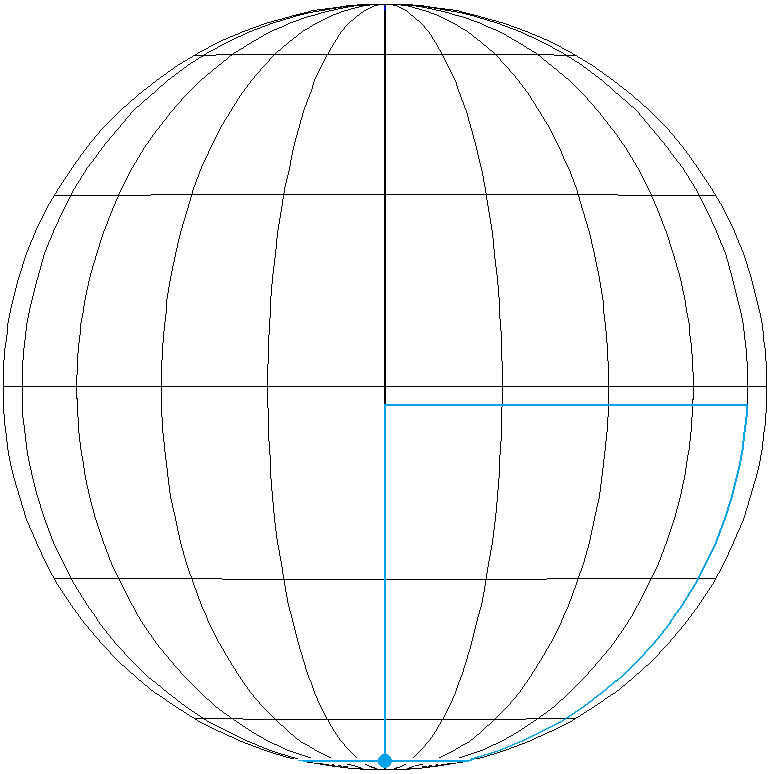
Example 5 (cf. Ex. 3):  Stage length \(~2000~\text{km}_~\),  with \(~k=-2_~\).

\(~d~\approx~8,99326°~~\widehat{=}~~1000~\text{km}\)

\(\phi~\approx~-79,6758°\)

The drone starts on latitude \(-88,6691°\).

First stage, going north, to latitude \(-70,6825°\).

Second stage (north stage) to the east covering \(~2_~d/\text{cos}~(\phi + d)~\approx~54,372°\) (longitude) with \(~k_1 = 0_~\).

Third stage, going south, to latitude \(-88,6691°\).

Fourth stage (south stage) to the west covering \(~2_~d/\text{cos}~(\phi - d)~\approx~774,372°~=~2 \cdot 360°+54,372°\) (longitude) with \(~k_2 = 2~\).


Südlösung

Figure 3  South solution with \(~k_1 = 0_~\);  the blue point is the starting point.


Assessment of the \(~k_i\)

We get the solutions of the problem by input of \(~d~\) and \(~k~\) (with \(~k = k_1-k_2\)). The \(~k_i~\) are the count of complete circuits along the north resp. the south circle. We want to calculate them from \(~d~\) and \(~k_~\).

In  table 1  we find the \(~d-\)values for which the north stage covers exactly \(~k_1~\) circuits along the north circle and the south stage covers exactly \(~k_2~\) circuits along the south circle; then the first and the third stage are identical.

The \(~d-\)values in the table are calculated with (6), (7), (8) and may be extended at the bottom and the right side of the table.

The table displays the symmetry of the north and the south solutions: The \(~d-\)values lie symmetrically to the main diagonal; \(~k_1~\) and \(~k_2~\) are interconvertible.

We calculate the limits in table 1 with (5): \[\text{North solution:}~~\lim_{k~\to~\infty}~\phi = \text{arcsin}~(\text{cos}~d) = 90° - d\] \[\text{South solution:}~~\lim_{k~\to~-\infty}~\phi = \text{arcsin}~(-\text{cos}~d) = d-90°\] \[~~~~~~\rightarrow~~~\lim_{k~\to~\pm~\infty}~\text{cos}~(\phi \mp d) = \text{cos}~(\pm(90° - 2_~d)) = \text{sin}~2_~d\] From (7) and (8) we get: \[\textbf{(9a)}~~~k_2~~\text{fixed:}~~~\lim_{k_1~\to~\infty}~2_~\pi~\text{cos}~(\phi - d) = 2_~\pi~\text{sin}~2_~d = \frac{2_~d}{k_2}\] \[\textbf{(9b)}~~~k_1~~\text{fixed:}~~~\lim_{k_2~\to~\infty}~2_~\pi~\text{cos}~(\phi + d) = 2_~\pi~\text{sin}~2_~d = \frac{2_~d}{k_1}\] The latter equations in (9a) and (9b) must be solved numerically and produce the limits at the bottom and the right border of table 1.

The limit \(~90°\) at the bottom right follows from (6) or (9a)/(9b) for \(~k_i~\rightarrow +\infty~\).


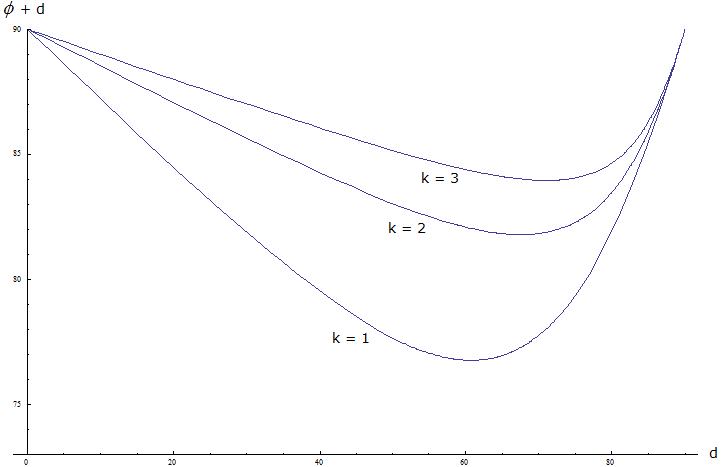
k1      k2 1 2 3 4 5 limit
1 67,8541° 72,3525° 73,9385° 74,7517° 75,2467° 77,2863°
2 72,3525° 77,5586° 79,4014° 80,3482° 80,9253° 83,3098°
3 73,9385° 79,4014° 81,3369° 82,3320° 82,9387° 85,4477°
4 74,7517° 80,3482° 82,3320° 83,3521° 83,9743° 86,5480°
5 75,2467° 80,9253° 82,9387° 83,9743° 84,6059° 87,2194°
limit 77,2863° 83,3098° 85,4477° 86,5480° 87,2194° 90°

Table 1   Angles \(~d~\) in green: The north stage covers exactly \(~k_1~\) circuits along the north circle and the south stage covers exactly \(~k_2~\) circuits along the south circle.


Example 6:  \(~k_1 = k_2 = 3~~\rightarrow~~d \approx 81,3369°~\) in table 1 relates to \(~s \approx 18088,43~\text{km}~\).  For shorter stages with \(~k = 0~\) (equator solution) are at most \(~2~\) complete circuits of north and south circles possible. For larger stages with \(~k = 0~\) the drone will cover at least \(~3~\) complete circuits on either circle.

Example 7:  \(~k_1 = 3,~~k_2 = 1~~\rightarrow~~d \approx 73,9385°~\) in table 1 relates to \(~s \approx 16443,10~\text{km}~\).  For shorter stages with \(~k = 2~\) (north solution) a complete circuit on the south circle is not possible (\(~k_1 = 2,~~k_2 = 0~\)). For larger stages with \(~k = 2~\) the drone will cover at least \(~1~\) complete circuit along the south circle (\(~k_2 \ge 1,~~k_1 = k_2+2~\)).

Example 8:  \(~k_1 = 2,~~k_2 = 3~~\rightarrow~~d \approx 79,4014°~\) in table 1 relates to \(~s \approx 17657,99~\text{km}~\).  For shorter stages with \(~k = -1~\) (south solution) the drone completes at most \(~1~\) circuit of the north circle (\(~k_1 \le 1,~~k_2 = k_1+1~\));  for larger stages it will cover at least \(~2~\) complete circuits (\(~k_1 \ge 2,~~k_2 = k_1+1~\)).

Example 9:  For \(~k_i = 1~\) table 1 shows the limit \(~77,2863°\);  it relates to \(~s \approx 17187,61~\text{km}~\).  For larger stages the longer latitude circle will be completely orbited at least twice. The other limits get their meaning in the same way: The limit in the \(~k_i^{th}\) row or column indicates that for bigger values of \(~d~\) the longer latitude circle will be completely orbited at least \(~(k_i+1)~\)times.


Conclusions
  • We start with a single input: A half-stage expressed by the angle \(~d~\).  The output should be a latitude circle from which the journey starts (the exact position on this circle is not relevant to this problem).

  • The solution is far from being unique. We find a countable infinite set of solutions  –  these can be numbered by \(~k \in \textbf{Z}_~\).

  • \(k = 0~\) gives a solution with a starting point on latitude \(-d~\) with north and south stages lying symmetrically to the equator. This is the obvious and mostly quite rapidly given answer by problem solvers. It results from (4). We call it  "equator solution".

  • \(~k \gt 0~\) lead to pairwise different solutions with north and south stages lying symmetrically to a latitude circle north of the equator. These solutions result from the central equation (5) and are denoted by  "north solutions".

  • \(~k \lt 0~\) lead to pairwise different solutions with north and south stages lying symmetrically to a latitude circle south of the equator. These solutions also result from (5) and are denoted by  "south solutions".

  • In some examples above we studied very large stages nearly going round the earth. The very few references to this problem in the literature (including online sources) always give examples for small stages such as \(~1~\text{Mile}~\) or \(~100~\text{km}~\).  With the notion standard case we shall now discuss only "not too large" stages:

    Standard case

    • In the equator solution north and south circle are only partly covered by the flight of the drone.

    • In the north solutions the north circle will be completely orbited \(~k~\)times and then on a section of this latitude circle. The south circle is only partly covered by the voyage.

    • In the south solutions the north circle is only partly covered by the voyage. The south circle will be completely orbited \(~(-k)~\)times and then on a section of this latitude circle.

    • What is meant in this standard case by "not too large" stages? Table 1 informs us that \(~d \lt 67,8541°~\) relating to a stage length \(~s \lt 15090~\text{km}_~\).

    • If one is only interested in the north and south solutions the standard case can be extended to \(~d \lt 72,3525°~\) (see table 1) and \(~s \lt 16090,39~\text{km}_~\).  This is not true for the equator solution: For \(~67,8541° \lt d \lt 72,3525°~\) the north and the south circle will each be completely orbited once and then on a section of these circles.

  • We saw that other cases can only appear with very large stages. Starting with the standard case an increasing \(~d~\) will result in:

    • \((k_1,_~k_2) = (0,0)~\) for small \(~d~\),  then \(=(1,1)~\),  then \(=(2,2)~\) etc. (equator solution);

    • \((k_1,_~k_2) = (k,0)~~\rightarrow~~(k+1,_~1)~~\rightarrow~~(k+2,_~2)\) etc. (north solutions);

    • \((k_1,_~k_2) = (0,k)~~\rightarrow~~(1,_~k+1)~~\rightarrow~~(2,_~k+2)\) etc. (south solutions).

    • These "steps" correspond to the \(~d~\) in table 1.  –  In the first row and the first column we find the values of \(~d~\) below which the longer latitude circle will not be completely orbited.


Example 10:  One example introducing the problem had \(~s = 100~\text{km}~\).  In the same manner as in example 1 the equator solution has a starting point \(~50~\text{km}~\) south of the equator on latitude \(~-d~\approx -0,44966°\).  North and south stages cover ca. \(0,89935~\) degrees of longitude. (Equator solution - standard case; \(~k = k_1 = k_2 = 0~\).)

The north solution for \(~k = 1~\) has its starting point on the south circle \(~88,9751°\).  The first stage goes north to the north circle \(~89,8744°\);  there the drone flies east over \(~410,2775~\) degrees of longitude, eventually getting to the longitude \(~50,2775°\).  From there the voyage on its third stage proceeds to the south circle and covers there \(~100~\text{km}~\),  going west along \(~50,2775~\) degrees of longitude back to the starting point at longitude \(~0°\). (North solution - standard case; \(~k = k_1 = 1,~~k_2 = 0~\).)

The north solution for \(~k = 2~\) has its starting point on the south circle \(~89,0340°\).  The first stage goes north to the north circle \(~89,9334°\);  there the drone flies east over \(~773,3462~\) degrees of longitude, eventually getting to the longitude \(~53,3462°\).  From there the voyage on its third stage proceeds to the south circle and covers there \(~100~\text{km}~\),  going west along \(~53,3462~\) degrees of longitude back to the starting point at longitude \(~0°\). (North solution - standard case; \(~k = k_1 = 2,~~k_2 = 0~\).)

With \(~k~\) further increased, north and south circles move further to the north. (North solution - standard case; \(~k = k_1,~~k_2 = 0~\).)

The south solutions lie symmetrically to the north solutions. One has to change the sign of the latitudes and to swap north and south. (South solution - standard case; \(~k = k_2,~~k_1 = 0~\).)

Example 11:  Which input values for \(~d~\) and \(~k~\) yield a stage going along the equator (of course not along a complete circuit)?  In (5) we have then \(~d = \pm_~\phi~\).  E.g. for \(~k=1~\) we get the numerical solution \(~d~\approx~39,7854°\) with the north circle at \(~79,5709°\); the stages have the length ca. \(8847,84~\text{km}~\).  (North solution - standard case; \(~k_1 = 1,~~k_2 = 0~\).)

Another example has \(~k = -100~~~\rightarrow~~~ d \approx 44,9287°\) with the south circle at \(~-89,8573°\); the stages have the length ca. \(9991,64~\text{km}~\). (South solution - standard case; \(~k_1=0,~k_2 = 100~\).)


We close the topic of the N-E-S-W voyage with a special aspect: The smaller circles in the north and south solutions cannot have small latitudes. What does that exactly mean?

Moving \(~d~\) within the interval \(~(0°,90°)~\) we see that in the north solution the smaller (north) circle never has a latitude \(~\phi + d~\) below ca. \(~76,77°\);  the corresponding south solution has a smaller (south) circle \(~\phi - d~\) not above ca. \(~-76,77°\). More exact values are given in figure 4:

Minimum für kleine Breitenkreise

Figure 4  Positions of the north circles \(~\phi + d~\) in the north solutions for \(~k = 1,2,3~\) as a function of \(~d~\)

\(~~~~~~~~~~~~~~~~~k=1~~~\rightarrow~~~(\phi+d)_{min} = 76,7731°\) for \(~d \approx 60,7661°\)

\(~~~~~~~~~~~~~~~~~k=2~~~\rightarrow~~~(\phi+d)_{min} = 81,7904°\) for \(~d \approx 67,5916°\)

\(~~~~~~~~~~~~~~~~~k=3~~~\rightarrow~~~(\phi+d)_{min} = 83,9545°\) for \(~d \approx 71,0802°\)



Literature

[1]  Alfred Posamentier, Wolfgang Schulz:  The Art of Problem Solving: A Resource for the Mathematics Teacher, Corvin 1996; ch. "Symmetry Saves the Solution", section "Square Hunting"



Comments are welcome.


Last update 2022-07-25

blog overview   |    previous article   |    next article


Manfred Börgens   |   main page