Dodekaeder    MB Matheblog # 28 Inhalt Blog
voriger Eintrag    nächster Eintrag		 zur Leitseite
Index der gesamten Website

2023-08-14 union jack  english version


Nord - Ost - Süd - West                    Kommentare sind willkommen.


Ein altes und weithin bekanntes Problem lässt einen Wanderer \(~10~\text{km}~\) nach Süden, dann \(~10~\text{km}~\) nach Osten, dann \(~10~\text{km}~\) nach Norden gehen und an seinem Startpunkt ankommen. Man findet es in vielen Büchern und an zahlreichen Stellen im Internet. Es wird behauptet, dass Microsoft Bewerber damit konfontiert hat, und dass in jüngerer Zeit Elon Musk dasselbe tat. Wer es noch nicht kennt, kann es auf der sehr verdienstvollen Website des Buchautors und YouTubers Presh Talwalkar nachlesen, im Blog-Post vom 2011-02-22. Das Problem zählt zu den Klassikern, weil die meisten Problemlöser recht schnell die naheliegende Lösung finden; die Zufriedenheit mit dieser Leistung verhindert dann oft, dass andere, nicht so naheliegende Lösungen erkannt werden; und auch bei diesen kann es vorkommen, dass sie nicht in ihrer Gesamtheit überblickt werden.  –  All das macht den Reiz dieses alten Problems aus, und in diesem Blogbeitrag soll nun ein ganz ähnliches Problem diskutiert werden, das eine ebenso tiefe Staffelung von Lösungen bereithält, aber mathematisch deutlich anspruchsvoller und daher noch interessanter ist.

Hier ist das Problem:

Eine Drohne fliegt \(~100~\text{km}~\) nach Norden, dann \(~100~\text{km}~\) nach Osten, dann \(~100~\text{km}~\) nach Süden, dann \(~100~\text{km}~\) nach Westen und kommt an ihrem Startpunkt an.

Gefragt ist nach dem Breitenkreis, auf dem der Startpunkt liegt. Natürlich soll die Fragestellung nicht nur für die Etappenlänge \(~100~\text{km}~\) beantwortet werden, sondern allgemein für alle Etappen, die kürzer als der halbe Erdumfang sind (falls es eine Lösung für alle diese Etappenlängen gibt!).

Versuchen Sie nun selbst, eine oder mehrere Lösungen zu finden, bevor Sie weiterlesen.

A. Posamentier und W. Schulz behandeln das Problem in ihrem Buch  The Art of Problem Solving [1],  aber der dort vorgestellte Lösungsweg wurde nicht von ihnen selbst gefunden; im Buch wird auf ältere Quellen verwiesen, zurückgehend bis 1959. Die Autoren zeigen den Lösungsweg nicht vollständig auf, aber immerhin bis zu einer Stelle, von der aus man alleine fortfahren kann.

Im folgenden Kasten sollten die Rahmenbedingungen und einige Definitionen angegeben werden:

  • Die Erde soll als kugelförmig mit einem Umfang von \(~40030~\text{km}~\) angenommen werden.

  • Die Breitengrade liegen im Intervall \(~[-90°,_~90°]~\).  Die Längengrade liegen im Intervall \(~[_~0°,_~360°)~\),  Zählung ostwärts.

  • Im Problem kommen vier Etappen vor:

    • 1. Etappe nach Norden entlang eines Meridians; der Einfachheit halber soll dies der \(~0°-\)Meridian sein; man hätte auch jeden anderen nehmen können.

    • 2. Etappe ("Nordetappe") nach Osten entlang eines Breitenkreises ("Nord-Breitenkreis").

    • 3. Etappe nach Süden entlang eines Meridians.

    • 4. Etappe ("Südetappe") nach Westen entlang eines Breitenkreises ("Süd-Breitenkreis"); dieser ist identisch mit dem Breitenkreis, auf dem der Startpunkt liegt und gibt die Lösung des Problems.

    • Die Begriffe Nord- und Süd-Breitenkreis haben nichts zu tun mit Nord- und Südhalbkugel !

    • Eine Etappenlänge soll mit \(~s~\) bezeichnet werden und in \(~\text{km}~\) angegeben werden.

  • Nord- und Südbreitenkreis sollen in der Form \(~\phi + d~\) und \(~\phi - d~\) mit \(~d \in (0°,_~90°)\) angegeben werden. \(~\phi~\) ist also der Mittelwert der Breitengrade der beiden Kreise. Die gesuchte Lösung ist \(~\phi - d~\).

    \(s~\) und \(~d~\) lassen sich leicht ineinander umrechnen. \(~d~\) entspricht einer halben Etappe entlang eines Meridians: \[d = (s/80060) \cdot 360°~~~~~~~~~s = (d/360°) \cdot 80060\] Der Lösungsweg wird nur auf \(~d~\) zurückgreifen; lediglich in den Rechenbeispielen wird auch \(~s~\) angegeben. Das hat den Vorteil, dass \(~d~\) als Eingabewert für das Problem unabhängig vom Kugelumfang ist; die obige Umrechnung kann dann leicht auch für andere Umfänge angepasst werden.


Nord- bzw. Süd-Breitenkreis haben den Umfang \(~40030 \cdot \text{cos}_~(\phi \pm d)~\text{km}~\),  das entspricht der Distanz entlang einer Orthodromen von \(~360° \cdot \text{cos}_~(\phi \pm d)~\) als Zentrums-Winkel (d.h. Scheitel des Winkels im Erdmittelpunkt). Auf ihnen wird jeweils eine Etappe mit der Streckenlänge \(~2_~d~\) durchfahren.

Hier ist Vorsicht angebracht: Dieser Kreisumfang sowie \(~d~\) sind Distanzen auf der Kugel, die über einen Großkreis gemessen und bequemerweise als Zentrums-Winkel angegeben werden. Das bedeutet insbesondere, dass auf einem Breitenkreis die Angabe des Winkels \(~2_~d~\) nicht das Intervall der dort überdeckten Längengrade darstellt, denn der Breitenkreis ist kein Großkreis (mit Ausnahme des Äquators).

Der Quotient \(~q = (2_~d)/(360° \cdot \text{cos}_~(\phi \pm d))~\) gibt also an, wie oft Nord- bzw. Süd-Breitenkreis umfahren werden. Da die Längengrade auf diesen Kreisen die Werte \(~0°~\) bis \(~360°~\) durchlaufen, gibt \(~q \cdot 360°~\) an, wieviele Längengrade auf einer Etappe überschritten werden. Dies führt auf den Start des Lösungswegs in (1) und (2):

\[\textbf{(1)}~~~\text{Überschrittene Längengrade auf Nordetappe:}~~\frac{2_~d}{\text{cos}~(\phi + d)}\] \[~~~~~~~~~~~~~~~\text{Längengrad am Ende der Nordetappe:}~~~\lambda_1 = \frac{2_~d}{\text{cos}~(\phi + d)} - 2_~k_{1~} \pi\] \[~~~~~~~~~~~~~~~k_1~~\text{vollständige Umläufe Richtung Ost}\]
\[\textbf{(2)}~~~\text{Überschrittene Längengrade auf Südetappe:}~~\frac{2_~d}{\text{cos}~(\phi - d)}\] \[~~~~~~~~~~~~~~~\text{Längengrad am Ende der Südetappe:}~~~\lambda_2 = \lambda_1 -\frac{2_~d}{\text{cos}~(\phi - d)} + 2_~k_{2~} \pi\] \[~~~~~~~~~~~~~~~k_2~~\text{vollständige Umläufe Richtung West}\]
Damit man an den Startpunkt zurückkehrt, muss \(~\lambda_2 = 0~\) sein: \[\textbf{(3)}~~~\lambda_2 = 0~~~~\Rightarrow~~~~\frac{1}{\text{cos}~(\phi + d)} - \frac{1}{\text{cos}~(\phi - d)} = \frac{k_~\pi}{d}~~~~\text{mit}~~~~k = k_1-k_2\] Wir formen um: \[\textbf{(4)}~~~\frac{k_~\pi}{d} = \frac{\text{cos}~(\phi - d) - \text{cos}~(\phi + d)}{\text{cos}~(\phi + d) \cdot \text{cos}~(\phi - d)} = 4 \cdot \frac{\text{sin}~\phi \cdot \text{sin}~d}{\text{cos}~2_~\phi~+~\text{cos}~2_~d} = 2 \cdot \frac{\text{sin}~\phi \cdot \text{sin}~d}{\text{cos}^2~d~-~\text{sin}^2~\phi}\]
Erste Lösung  ("Äquatorlösung") :  \(~k=0\)

Mit (4) erhalten wir \(~\phi = 0~\),  starten also südlich des Äquators auf dem Breitengrad \(~-d_~\).

Wegen \(~k_1 = k_2~\) werden auf Nord- und Süd-Breitenkreis gleich viele volle Umläufe gemacht.
Beispiel 1:  Es werden in jeder Himmelsrichtung \(~800~\text{km}~\) zurückgelegt.

\(~d~\approx~3,5973°~~\widehat{=}~~400~\text{km}\)

Nochmal der Hinweis: Die Angabe in Grad gilt für einen Großkreis auf der Kugel, also hier für die 1. und 3. Etappe; sie bezieht sich nicht auf die Längengrade auf der Nord- und Südetappe.

Auf den Nord- und Süd-Breitenkreisen, also in Ost- bzw. Westrichtung, werden jeweils \(~2_~d/\text{cos}~(\pm d)~\approx~7,2088°\) (Längengrade) überschritten, also ist \(~k_1 = k_2=0~\).
Beispiel 2:  Es werden in jeder Himmelsrichtung \(~18000~\text{km}~\) zurückgelegt.

\(~d~\approx~80,9393°~~\widehat{=}~~9000~\text{km}\)

In Ost- bzw. Westrichtung werden jeweils \(~2_~d/\text{cos}~(\pm d)~\approx~1027,926°~=~2 \cdot 360°+307,926°\) (Längengrade) überschritten, also ist \(~k_1 = k_2=2~\).


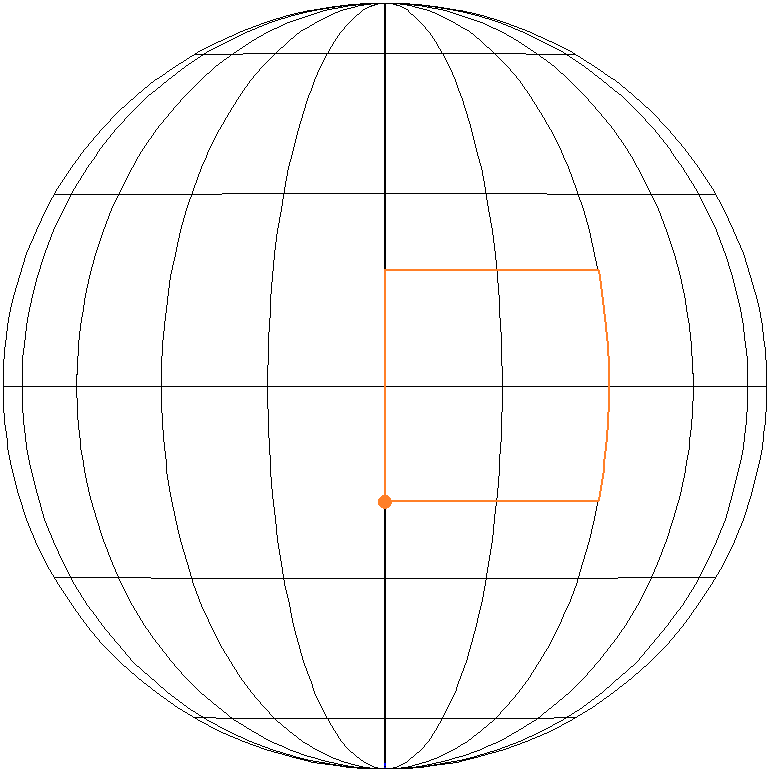
Äquatorlösung

Bild 1  Äquatorlösung mit \(~k_i = 0~\);  der orangene Punkt ist der Startpunkt.


Wir machen weiter mit (4) für \(~k \neq 0~\) und erhalten die quadratische Gleichung \[\text{sin}^2~\phi~+~\frac{2_~d}{k_~\pi}~\text{sin}~d~_~\text{sin}~\phi~-~\text{cos}^2~d~=~0\] \[\text{sin}~\phi~=~-\frac{d}{k_~\pi}~\text{sin}~d~\pm~\sqrt{\frac{d^{~2}}{k^2_~\pi^2}~\text{sin}^2~d~+~\text{cos}^2~d~}\] \[\textbf{(5)}~~~\phi~=~\text{arcsin}\left(-\frac{d}{k_~\pi}~\text{sin}~d~\pm~\sqrt{\frac{d^{~2}}{k^2_~\pi^2}~\text{sin}^2~d~+~\text{cos}^2~d~}\right)\]
Zweite Lösung  ("Nordlösung") :  \(~k \gt 0\)

Wegen \(~k_1 \gt k_2~\) wird der Nordbreitenkreis häufiger umlaufen  –  und ist deshalb kürzer  –  als der Südbreitenkreis. Also ist \(~\phi \gt 0~\).  In (5) kommt somit nur die "+"-Lösung in Frage.
Beispiel 3:  Es werden in jeder Himmelsrichtung \(~2000~\text{km}~\) zurückgelegt, mit \(~k=2~\).

\(~d~\approx~8,9933°~~\widehat{=}~~1000~\text{km}\)

\(\phi~\approx~79,6758°\)

Start auf Breitengrad \(70,6825°\).

Erste Etappe nach Norden auf Breitengrad \(88,6691°\).

Zweite Etappe nach Osten über \(~2_~d/\text{cos}~(\phi + d)~\approx~774,372°~=~2 \cdot 360°+54,372°\) (Längengrade); also ist \(~k_1 = 2~\).

Dritte Etappe nach Süden auf Breitengrad \(70,6825°\).

Vierte Etappe nach Westen über \(~2_~d/\text{cos}~(\phi - d)~\approx~54,372°\) (Längengrade); also ist \(~k_2 = 0~\).
Beispiel 4:  Es werden in jeder Himmelsrichtung \(~16250~\text{km}~\) zurückgelegt, mit \(~k=1~\).

\(~d~\approx~73,0702°~~\widehat{=}~~8125~\text{km}\)

\(\phi~\approx~5,5693°\)

Start auf Breitengrad \(-67,5009°\).

Erste Etappe nach Norden auf Breitengrad \(78,6395°\).

Zweite Etappe nach Osten über \(~2_~d/\text{cos}~(\phi + d)~\approx~741,898°~=~2 \cdot 360°+21,898°\) (Längengrade); also ist \(~k_1 = 2~\).

Dritte Etappe nach Süden auf Breitengrad \(-67,5009°\).

Vierte Etappe nach Westen über \(~2_~d/\text{cos}~(\phi - d)~\approx~381,898°~=~360°~+~21,898°\) (Längengrade); also ist \(~k_2 = 1~\).


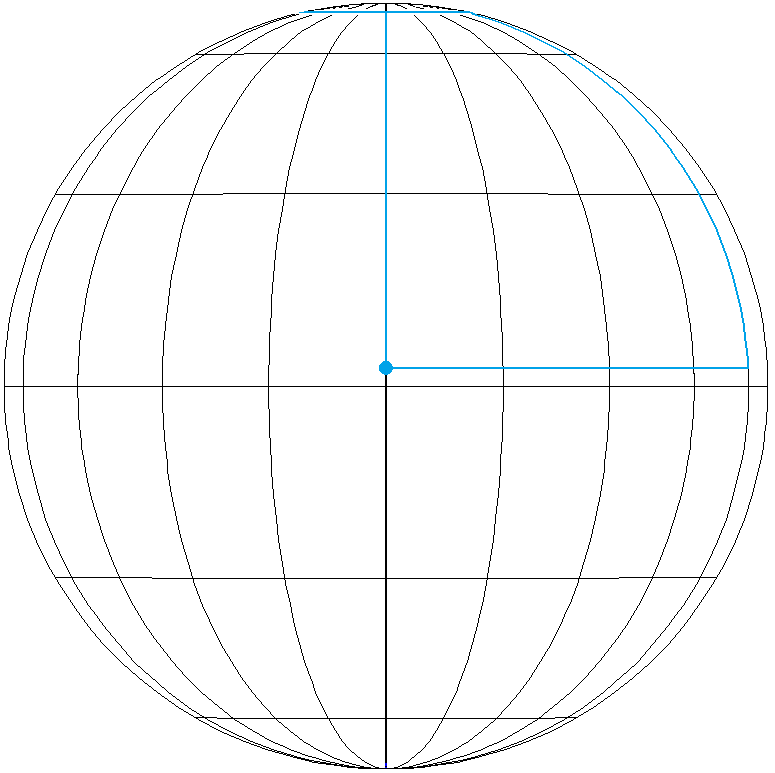
Nordlösung

Bild 2  Nordlösung mit \(~k_2 = 0~\);  der blaue Punkt ist der Startpunkt.


Dritte Lösung  ("Südlösung") :  \(~k \lt 0\)

Wegen \(~k_1 \lt k_2~\) wird der Südbreitenkreis häufiger umlaufen  –  und ist deshalb kürzer  –  als der Nordbreitenkreis. Also ist \(~\phi \lt 0~\).  In (5) kommt somit nur die "–"-Lösung in Frage.  —  Die zweite und die dritte Lösung liegen symmetrisch zum Äquator.
Beispiel 5 (vgl. Beispiel 3):  Es werden in jeder Himmelsrichtung \(~2000~\text{km}~\) zurückgelegt, mit \(~k=-2~\).

\(~d~\approx~8,99326°~~\widehat{=}~~1000~\text{km}\)

\(\phi~\approx~-79,6758°\)

Start auf Breitengrad \(-88,6691°\).

Erste Etappe nach Norden auf Breitengrad \(-70,6825°\).

Zweite Etappe nach Osten über \(~2_~d/\text{cos}~(\phi + d)~\approx~54,372°\) (Längengrade); also ist \(~k_1 = 0~\).

Dritte Etappe nach Süden auf Breitengrad \(-88,6691°\).

Vierte Etappe nach Westen über \(~2_~d/\text{cos}~(\phi - d)~\approx~774,372°~=~2 \cdot 360°+54,372°\) (Längengrade); also ist \(~k_2 = 2~\).


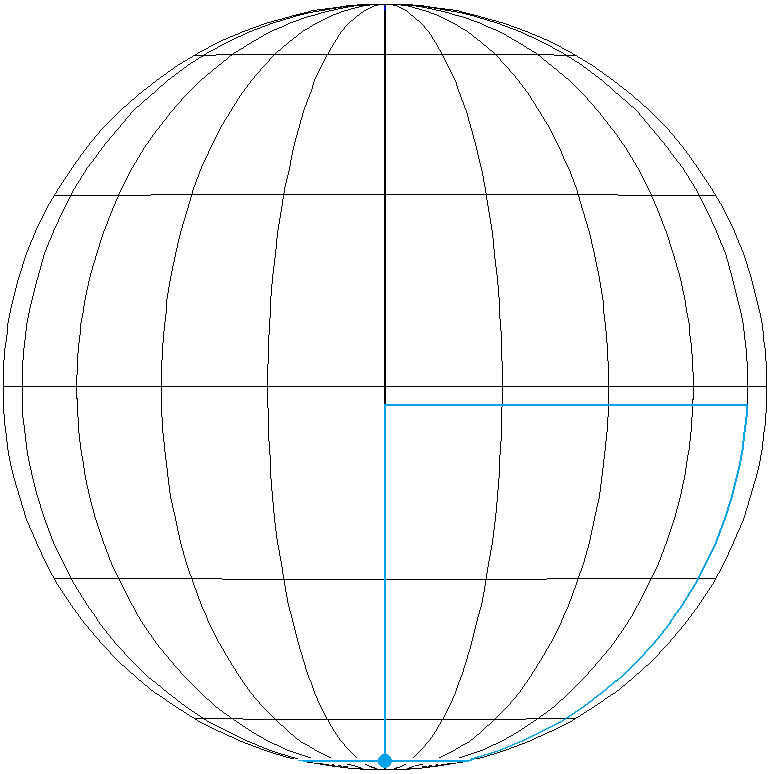
Südlösung

Bild 3  Südlösung mit \(~k_1 = 0~\);  der blaue Punkt ist der Startpunkt.


Bestimmung der \(~k_i\)

Lösungen des Problems erhält man durch Vorgabe von \(~d~\) und \(~k~\) (mit \(~k = k_1-k_2\)). Die \(~k_i~\) sind die Anzahlen der vollständigen Umläufe um Nord- bzw. Süd-Breitenkreis. Wie kann man sie aus \(~d~\) und \(~k~\) berechnen?

In Tabelle 1 sind die \(d~\) angegeben, bei denen der Nordbreitenkreis exakt \(~k_1-\)mal und der Sübreitenkreis exakt \(~k_2-\)mal durchlaufen wird, so dass die 1. und die 3. Etappe identisch sind.

Die Werte in der Tabelle werden mit (6), (7), (8) berechnet und lassen sich natürlich nach unten und nach rechts beliebig weit fortsetzen.

Die Symmetrie zwischen Nord- und Südlösung (s.o.) zeigt sich auch in der Tabelle: Die \(~d-\)Werte liegen symmetrisch zur Hauptdiagonalen, d.h. \(~k_1~\) und \(~k_2~\) sind vertauschbar.

Für die Berechnung der Grenzwerte ergibt sich mit (5): \[\text{Nordlösung:}~~\lim_{k~\to~\infty}~\phi = \text{arcsin}~(\text{cos}~d) = 90° - d\] \[\text{Südlösung:}~~\lim_{k~\to~-\infty}~\phi = \text{arcsin}~(-\text{cos}~d) = d-90°\] \[~~~~~~\rightarrow~~~\lim_{k~\to~\pm~\infty}~\text{cos}~(\phi \mp d) = \text{cos}~(\pm(90° - 2_~d)) = \text{sin}~2_~d\] Mit (7) und (8) folgt: \[\textbf{(9a)}~~~k_2~~\text{fest:}~~~\lim_{k_1~\to~\infty}~2_~\pi~\text{cos}~(\phi - d) = 2_~\pi~\text{sin}~2_~d = \frac{2_~d}{k_2}\] \[\textbf{(9b)}~~~k_1~~\text{fest:}~~~\lim_{k_2~\to~\infty}~2_~\pi~\text{cos}~(\phi + d) = 2_~\pi~\text{sin}~2_~d = \frac{2_~d}{k_1}\] Die jeweils letzten Gleichungen in (9a) und (9b) werden numerisch gelöst und führen auf die Grenzwerte am unteren und am rechten Rand der Tabelle.

Der Grenzwert \(~90°~\) unten rechts folgt direkt aus (6) oder (9a)/(9b) für \(~k_i~\rightarrow +\infty~\).


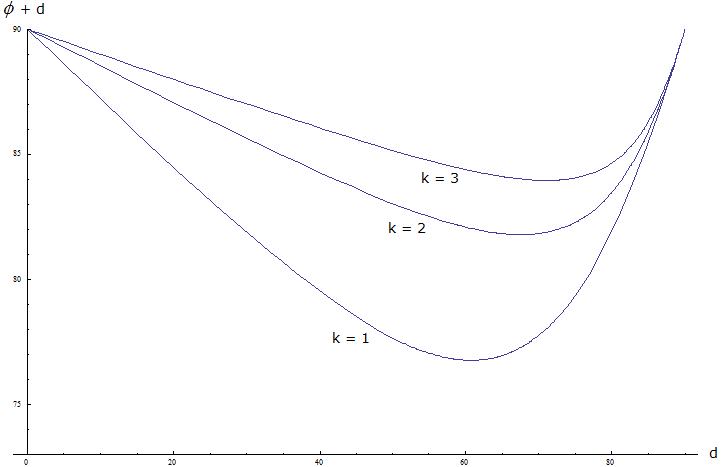
k1      k2 1 2 3 4 5 Grenzwert
1 67,8541° 72,3525° 73,9385° 74,7517° 75,2467° 77,2863°
2 72,3525° 77,5586° 79,4014° 80,3482° 80,9253° 83,3098°
3 73,9385° 79,4014° 81,3369° 82,3320° 82,9387° 85,4477°
4 74,7517° 80,3482° 82,3320° 83,3521° 83,9743° 86,5480°
5 75,2467° 80,9253° 82,9387° 83,9743° 84,6059° 87,2194°
Grenzwert 77,2863° 83,3098° 85,4477° 86,5480° 87,2194° 90°

Tabelle 1   Grün unterlegt stehen die Winkel \(~d~\),  bei denen der Nordbreitenkreis exakt \(~k_1-\)mal und der Südbreitenkreis exakt \(~k_2-\)mal durchlaufen wird.


Beispiel 6:  \(~k_1 = k_2 = 3~~\rightarrow~~d \approx 81,3369°~\) in Tabelle 1 entspricht \(~s \approx 18088,43~\text{km}~\).  Bei kleineren Etappen kommt für \(~k = 0~\) (Äquatorlösung) nur eine höchstens \(~2-\)fache Umrundung von Nord- und Süd-Breitenkreis vor, bei größeren Etappen eine mindestens \(~3-\)fache Umrundung.

Beispiel 7:  \(~k_1 = 3,~~k_2 = 1~~\rightarrow~~d \approx 73,9385°~\) in Tabelle 1 entspricht \(~s \approx 16443,10~\text{km}~\).  Bei kleineren Etappen kommt für \(~k = 2~\) (Nordlösung) keine vollständige Umrundung des Süd-Breitenkreises zustande (\(~k_1 = 2,~~k_2 = 0~\)),  bei größeren Etappen eine mindestens \(~1-\)fache Umrundung (\(~k_2 \ge 1,~~k_1 = k_2 + 2~\)).

Beispiel 8:  \(~k_1 = 2,~~k_2 = 3~~\rightarrow~~d \approx 79,4014°~\) in Tabelle 1 entspricht \(~s \approx 17657,99~\text{km}~\).  Bei kleineren Etappen kommt für \(~k = -1~\) (Südlösung) nur eine höchstens \(~1-\)fache Umrundung des Nord-Breitenkreises vor (\(~k_1 \le 1,~~k_2 = k_1+1~\)),  bei größeren Etappen eine mindestens \(~2-\)fache Umrundung (\(~k_1 \ge 2,~~k_2 = k_1+1~\)).

Beispiel 9:  Bei \(~k_i = 1~\) finden wir in Tabelle 1 den Grenzwert \(~77,2863°\),  er entspricht \(~s \approx 17187,61~\text{km}~\).  Bei größeren Etappen wird der größere Breitenkreis mindestens \(~2-\)mal umlaufen. Auch die anderen Grenzwerte lassen sich auf diese Weise interpretieren: Der Grenzwert in der \(~k_i-\)ten Zeile oder Spalte bedeutet, dass für größere \(~d-\)Werte der größere Breitenkreis mindestens \(~(k_i+1)-\)mal umlaufen wird.


Fazit
  • Vorgegeben ist die halbe Etappenlänge \(~d~\).  Es reicht, den Startbreitenkreis zu suchen (die Startposition auf diesem Kreis ist für das Problem unerheblich und kann beliebig gewählt werden).

  • Die Lösung ist nicht eindeutig. Ganz im Gegenteil: Es gibt abzählbar unendlich viele Lösungen, die sich mit \(~k \in \textbf{Z}~\) nummerieren lassen.

  • \(k = 0~\) führt auf eine Lösung, deren Start auf dem Breitengrad \(~-d~\) liegt und deren Nord- und Südetappe symmetrisch zum Äquator liegen. Dies ist die naheliegende und meist schnell gefundene Lösung. Sie ergibt sich aus (4). Wir nennen sie  "Äquatorlösung".

  • Die \(~k \gt 0~\) führen auf paarweise verschiedene Lösungen, deren Nord- und Südetappe symmetrisch zu einem Breitenkreis nördlich des Äquators liegen. Diese Lösungen ergeben sich aus der zentralen Gleichung (5) und werden mit  "Nordlösungen"  bezeichnet.

  • Die \(~k \lt 0~\) führen auf paarweise verschiedene Lösungen, deren Nord- und Südetappe symmetrisch zu einem Breitenkreis südlich des Äquators liegen. Sie ergeben sich ebenfalls aus (5) und werden mit  "Südlösungen"  bezeichnet.

  • Weiter oben wurden Beispiele mit geradezu riesigen Etappen betrachtet, die nahezu um den ganzen Globus führen. Bei den wenigen Erwähnungen des Problems in der Literatur ist immer von kleinen Etappen die Rede, wie \(~1~\text{Meile}~\) oder \(~100~\text{km}~\).  Als Standardfall wollen wir "nicht zu große" Etappen nehmen:

    Standardfall

    • Bei der Äquatorlösung werden Nord- und Südbreitenkreis nur teilweise umlaufen.

    • Bei den Nordlösungen wird der Nordbreitenkreis \(~k-\)mal vollständig umlaufen und dann noch auf einem weiteren Teilstück dieses Breitenkreises. Der Südbreitenkreis wird nur teilweise umlaufen.

    • Bei den Südlösungen wird der Nordbreitenkreis nur teilweise umlaufen. Der Südbreitenkreis wird \(~(-k)-\)mal vollständig umlaufen und dann noch auf einem weiteren Teilstück dieses Breitenkreises.

    • Was bedeutet "nicht zu große" Etappen in diesem Standardfall? Die Tabelle 1 gibt Auskunft: Es muss \(~d \lt 67,8541°~\) sein, das entspricht einer Etappenlänge \(~s \lt 15090~\text{km}~\).

    • Betrachtet man nur Nord- und Südlösung, so lässt sich der Standardfall nach Tabelle 1 noch auf \(~d \lt 72,3525°~\) und \(~s \lt 16090,39~\text{km}~\) ausdehnen. Im "Zwischenbereich" gilt das aber nicht für die Äquatorlösung: Dort werden dann Nord- und Südbreitenkreis jeweils einmal vollständig umlaufen und dann noch auf einem weiteren Teilstück dieser Breitenkreise.

  • Die anderen Fälle kommen also nur bei extrem großen Etappen vor. Ausgehend vom Standardfall geht bei kontinuierlicher Vergrößerung von \(~d\)

    • \((k_1,_~k_2) = (0,0)~\) erst über in \(~(1,1)\), dann in \(~(2,2)\) usw. (Äquatorlösung);

    • \((k_1,_~k_2) = (k,0)~\) erst über in \(~(k+1,_~1)\), dann in \(~(k+2,_~2)\) usw. (Nordlösungen);

    • \((k_1,_~k_2) = (0,k)~\) erst über in \(~(1,_~k+1)\), dann in \(~(2,_~k+2)\) usw. (Südlösungen).

    • Für welche \(~d~\) diese Schritte erfolgen, entnimmt man Tabelle 1.  –  In der ersten Zeile und der ersten Spalte stehen die \(~d-\)Werte, unterhalb derer der längere Breitenkreis nicht vollständig umrundet wird.


Beispiel 10:  Das einführende Beispiel war für \(~s = 100~\text{km}~\) formuliert. Analog zu Beispiel 1 beginnt die Äquatorlösung also \(~50~\text{km}~\) südlich des Äquators auf dem Breitengrad \(~-d~\approx -0,44966°\).  Nord-und Südetappen überspannen ca. \(0,89935~\) Längengrade. (Äquatorlösung - Standardfall; \(~k = k_1 = k_2 = 0~\).)

Die Nordlösung für \(~k = 1~\) beginnt am Startpunkt auf dem Süd-Breitenkreis \(~88,9751°~\).  Die erste Etappe führt auf den Nord-Breitenkreis \(~89,8744°~\) und führt dort über \(~410,2775~\) Längengrade nach Osten, so dass man bei der Länge \(~50,2775°~\) auskommt. Von dort geht es wieder auf den Süd-Breitenkreis und dort \(~100~\text{km}~\) zurück über \(~50,2775~\) Längengrade nach Westen bis zum Startpunkt auf \(~0°~\) Länge. (Nordlösung - Standardfall; \(~k = k_1 = 1,~~k_2 = 0~\).)

Die Nordlösung für \(~k = 2~\) beginnt am Startpunkt auf dem Süd-Breitenkreis \(~89,0340°~\).  Die erste Etappe führt auf den Nord-Breitenkreis \(~89,9334°~\) und führt dort über \(~773,3462~\) Längengrade nach Osten, so dass man bei der Länge \(~53,3462°~\) auskommt. Von dort geht es wieder auf den Süd-Breitenkreis und dort \(~100~\text{km}~\) zurück über \(~53,3462~\) Längengrade nach Westen bis zum Startpunkt auf \(~0°~\) Länge. (Nordlösung - Standardfall; \(~k = k_1 = 2,~~k_2 = 0~\).)

Erhöht man \(~k~\) weiter, so rücken Nord- und Süd-Breitenkreis weiter nach Norden. (Nordlösung - Standardfall; \(~k = k_1,~~k_2 = 0~\).)

Die Südlösungen liegen symmetrisch zu den Nordlösungen. Die Breitenkreise sind negativ zu nehmen unter Vertauschung von Nord und Süd. (Südlösung - Standardfall; \(~k = k_2,~~k_1 = 0~\).)

Beispiel 11:  Welche Eingabewerte \(~d~\) und \(~k~\) führen zu einer Etappe, die entlang des Äquators verläuft (natürlich nicht ganz rundum)? In (5) muss dann \(~d = \pm_~\phi~\) gelten. Z.B. für \(~k=1~\) ergibt sich die numerische Lösung \(~d~\approx~39,7854°\), so dass der Nord-Breitenkreis bei \(~79,5709°\) liegt; die Etappenlänge ist dann ca. \(8847,84~\text{km}~\).  (Nordlösung - Standardfall; \(~k_1 = 1,~~k_2 = 0~\).)

Nehmen wir als weiteres Beispiel \(~k = -100~~~\rightarrow~~~ d \approx 44,9287°\), so dass der Süd-Breitenkreis bei \(~-89,8573°\) liegt; die Etappenlänge ist dann ca. \(9991,64~\text{km}~\). (Südlösung - Standardfall; \(~k_1=0,~k_2 = 100~\).)


Zum Abschluss noch ein spezieller Aspekt: Wie nahe können die kleineren Breitenkreise in der Nord- und Südlösung dem Äquator kommen?

Variiert man \(~d~\) im Intervall \(~(0°,90°)~\),  so stellt man fest, dass bei der Nordlösung der kleinere (nördliche) Breitenkreis \(~\phi + d~\) nie südlicher als ca. \(~76,77°\) liegt; entsprechend liegt bei der Südlösung der kleinere (südliche) Breitenkreis \(~\phi - d~\) nie nördlicher als ca. \(~-76,77°\). Exaktere Werte liefert Bild 4:

Minimum für kleine Breitenkreise

Bild 4  Lage der nördlichen Breitenkreise \(~\phi + d~\) in den Nordlösungen für \(~k = 1,2,3~\),  in Abhängigkeit von \(~d~\)

\(~~~~~~~~~~~~~~~~~k=1~~~\rightarrow~~~(\phi+d)_{min} = 76,7731°\) für \(~d \approx 60,7661°\)

\(~~~~~~~~~~~~~~~~~k=2~~~\rightarrow~~~(\phi+d)_{min} = 81,7904°\) für \(~d \approx 67,5916°\)

\(~~~~~~~~~~~~~~~~~k=3~~~\rightarrow~~~(\phi+d)_{min} = 83,9545°\) für \(~d \approx 71,0802°\)



Quelle

[1]  Alfred Posamentier, Wolfgang Schulz:  The Art of Problem Solving: A Resource for the Mathematics Teacher, Verlag Corvin 1996; Kap. "Symmetry Saves the Solution", Abschnitt "Square Hunting"



Kategorie: Geomathematik                    Kommentare sind willkommen.


Stand 2022-07-14

Inhalt Blog   |    voriger Eintrag   |    nächster Eintrag

Manfred Börgens   |   Zur Leitseite