Dodekaeder    MB Matheblog # 29 Inhalt Blog
voriger Eintrag    nächster Eintrag		 zur Leitseite
Index der gesamten Website


2023-09-27


Emil auf der Flucht  –  Teil 1                    Kommentare sind willkommen.


Für diesen Beitrag habe ich mit   Kevin Börgens, Chicago  zusammengearbeitet. Er hatte die Idee für die Problemstellung und hat die wesentlichen Teile der Mathematik für die Lösung geliefert.  –  Wir starten mit diesem Beitrag eine kleine Serie von verwandten Problemstellungen.

Auf der Website  FiveThirtyEight  wurde in der Rubrik  The Riddler  ein ähnliches Problem [1] gestellt, allerdings mit anderer Ausgangslage und entsprechend anderer Lösung. Diese Lösung [2] zeigte, dass die Aufgabenstellung nicht ganz glücklich gewählt war. Es war naheliegend, das Riddler-Problem als Anregung zur Suche nach einem modifizierten Szenario zu nehmen; dies mündete in die hier vorgelegte Version.


Auf dem Weg in die Freiheit läuft Emil durch einen langen dunklen Gang. In diesem wartet ein Wächter auf ihn, der ihn aber nur erkennen kann, wenn Emil in den Lichtschein seiner Laterne gerät. Beide haben einen klaren Plan:
Wir wollen die Situation von Emil und dem Wächter mathematisch formulieren:
Kurz nach dem Loslaufen

Bild 1   Hier und in den folgenden Bildern: Der linke Rand der Skizze ist die Mittellinie des Gangs, der rechte Rand der Skizze ist der rechte Rand des Gangs. Der Wächter und Emil laufen in der Skizze von unten nach oben. Wir wollen o.E. annehmen, dass Emil die rechte Wand gewählt hat. Der Wächter läuft im Winkel \(~\alpha~\) los.
Hier ist ein Zeitpunkt festgehalten, bei dem der Wächter die Strecke \(~t~\) vom Koordinatenursprung \(~O~\) bis \(~A~\) zurückgelegt hat. Emil läuft die Strecke \(~q~t~\) entlang der rechten Wand. Der Wächter ist noch nicht weit gekommen; der Lichtschein hat noch nicht die rechte Wand erreicht.

An dieser Stelle haben die Leser vielleicht Lust, nicht weiterzulesen, sondern selbst herauszufinden, wie Emils Flucht weitergeht und ob er dem Wächter entkommt, falls dieser sich optimal verhält.

Dickpunkt   Falls Emil nicht schneller als der Wächter ist, kann er nicht sicher entkommen.

D.h. wir brauchen nur \(~q \gt 1~\) zu betrachten. Warum ist das so? Der Wächter kennt ja \(~q~\) nicht, aber Emil muss damit rechnen, dass der Wächter mehr oder weniger zufällig einen Richtungswinkel \(~\alpha~\) einschlägt, der ihn Emil erwischen lässt. Bild 2 zeigt, wie das für \(~q \le 1~\) geht: Er läuft maximal die Streckenlänge \(~t=(v^2-r^2)~/~(2~r)~\) (Pythagoras!) mit dem Richtungswinkel \(~\alpha = \text{arctan}~(t/v)~\) und bleibt dann stehen. Für \(~q = 1~\) stellt der Wächter Emil im letzten Moment, für \(~q \lt 1~\) gerät Emil schon früher in den Lichtschein.  –  Wir werden allerdings später sehen, dass der Wächter den Winkel keineswegs zufällig wählen wird.

q=1

Bild 2   Wenn Emil höchstens so schnell wie der Wächter läuft, gibt es einen Winkel \(~\alpha~\),  der zu Emils Ergreifung führt.

Nun soll also \(~q \gt 1~\) gelten, d.h. Emil läuft schneller als der Wächter. Bild 3 zeigt links den Zeitpunkt, an dem der Lichtschein die Wand berührt. Emil hat diesen Punkt bereits hinter sich gelassen, denn ist \(~t_1~\) die Strecke, die der Wächter zurückgelegt hat, so ist Emils \(~y-\)Koordinate \(~q~t_1 \gt t_1~\) und die \(~y-\)Koordinate des Kontaktpunkts \(~B_1~\) ist \(~t_1~\text{sin}~\alpha \lt t_1~\).  Was passiert nach diesem Zeitpunkt? Emil läuft in der rechten Skizze weiter nach oben, und da der Wächter sich weiter auf die Wand zubewegt, beleuchtet die Laterne eine ganze Strecke entlang der Wand, die zunehmend größer wird und deren oberes Ende \(~B_2~\) ebenfalls weiter nach oben wandert.

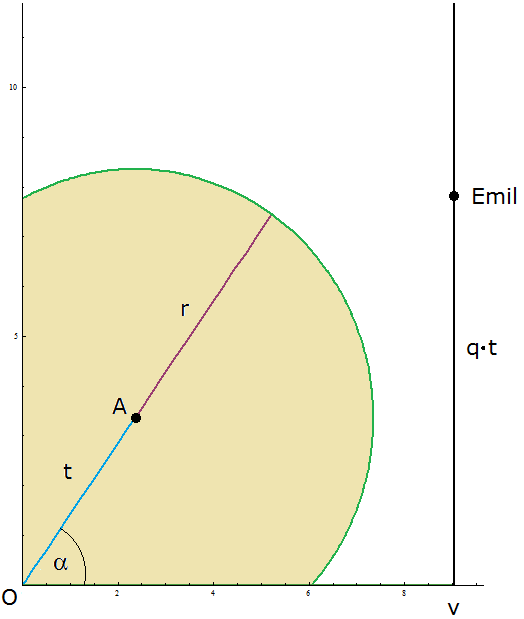
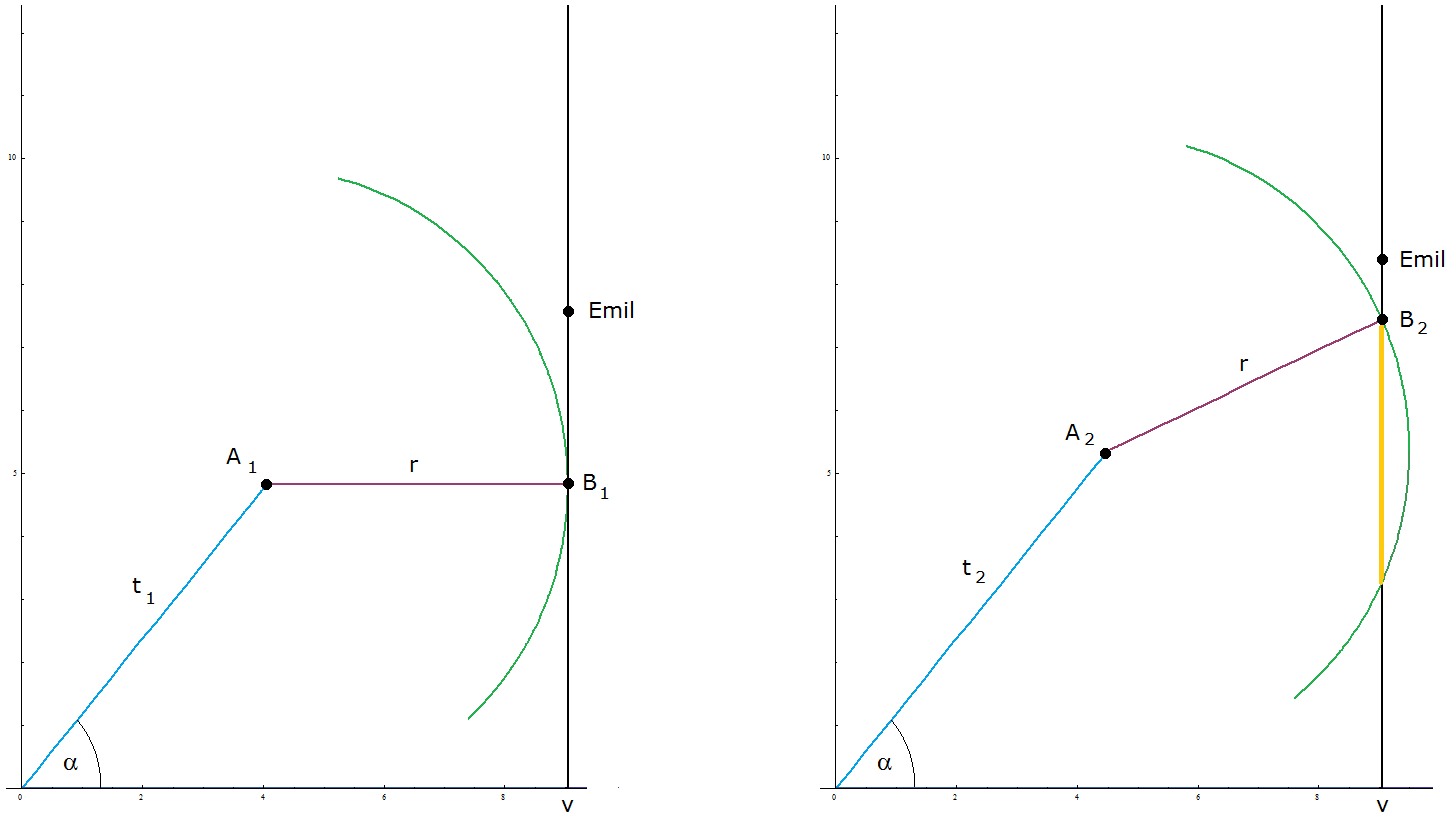
Erstkontakt und danach

Bild 3   Links: Erstkontakt des Lichtscheins mit der Wand.   Rechts: Etwas später. Der orangene Teil der Wand wird von der Laterne beschienen. Emil wurde vom Lichtschein noch nicht erreicht.

Wir können also festhalten:

Dickpunkt   Emil läuft vor dem Lichtschein her. Falls er erwischt wird, geschieht das, indem ihn der obere Rand des Lichtscheins an der Wand erreicht.

Kann Emil entkommen? Wenn man ein paar Werte für die vorkommenden Parameter ausprobiert, erkennt man schnell, dass beides geschehen kann: Emils Flucht gelingt, oder aber er wird vom Wärter gestellt, allerdings nur, wenn sich der Wächter richtig verhält. Das soll jetzt genauer untersucht werden.

Als Grenzgeschwindigkeit wollen wir die Geschwindigkeit definieren, bei der Emil gefasst wird, falls sich der Wächter optimal verhält, aber Emil bei größerer Geschwindigkeit unabhängig vom Verhalten des Wächters entkommt. Zur Grenzgeschwindigkeit soll der Faktor \(~q_{~\text{lim}}~\) gehören.

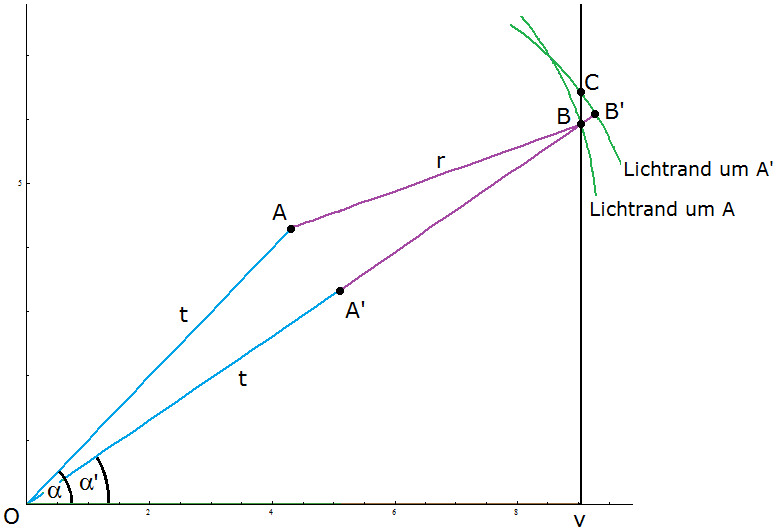
Wir nehmen nun an, dass Emil mit dem \(~q-\)fachen der Geschwindigkeit des Wächters läuft und gefasst wird. Bild 4 zeigt dafür zwei Konstellationen, in denen der Winkel \(~\beta \neq \alpha~\) ist. Es wird gezeigt werden, dass Emil dann nicht in der Grenzgeschwindigkeit läuft, sondern langsamer.

beta ungleich alpha

Bild 4   Beide Skizzen halten einen Zeitpunkt fest, an dem Emil in den Lichtschein gerät. Links ist \(~\beta \lt \alpha~\),  rechts ist \(~\beta \gt \alpha~\).  Emil befindet sich auf \(~B~\) mit der \(~y-\)Koordinate \(~q~t~\).

Ausgehend von Bild 4 werden wir einen anderen Winkel \(~\alpha'~\) angeben, der ebenfalls zu Emils Ergreifung führt, aber ein größeres \(~q~\) erlaubt. Wir beschränken uns auf die linke Skizze, da die Argumentation für die rechte Skizze ganz analog läuft. Wir verbinden \(~O~\) und \(~B~\) durch eine direkte Strecke, siehe Bild 5. \(~A'~\) entsteht durch Abtragen von \(~t~\).  Dann ist \(~A'B \lt r~\).  Wir verlängern \(~OA'B~\) bis \(~B~'~\),  sodass \(~A'B~' = r~\) ist. Der Lichtschein, der von \(~A'~\) ausgeht, hat seinen oberen Kontaktpunkt mit der Wand beim Punkt \(~C~\) oberhalb von \(~B~\) und damit von Emil. Er muss also schon früher in den Lichtschein um \(~A'~\) geraten sein und wäre somit auch bei einer größeren Geschwindigkeit vom Licht erfasst worden. Es folgt \(~q \lt q_{~\text{lim}}~\).

alpha'

Bild 5   Der Wächter ist mit dem Winkel \(~\alpha~\) losgelaufen und hat den Punkt \(~A~\) erreicht. Emil ist beim Punkt \(~B~\) angekommen und gerät gerade in den Lichtschein. Hätte der Wächter den Winkel \(~\alpha'~\) eingeschlagen, wäre der obere Rand des Lichtscheins an der Wand im Punkt \(~C~\) und Emil wäre schon vorher ins Licht geraten.

Aus den Bildern 4 und 5 schließen wir:

Dickpunkt   Wenn der Wächter Emil auch noch bei dessen Grenzgeschwindigkeit fassen will, muss er einen Startwinkel \(~\alpha~\) wählen, bei der \(~\alpha = \beta~\) ist.

Das bedeutet:
Bild 6 zeigt, dass diese Strategie des Wächters tatsächlich funktioniert. Zunächst ist zu beachten, dass sich in Bild 6 nichts Wesentliches ändern würde, wenn Emil langsamer laufen und der Wächter sein \(~\alpha~\) entsprechend anpassen würde. Die \(~y-\)Koordinate von Emil wäre dann \(~t~q~\).  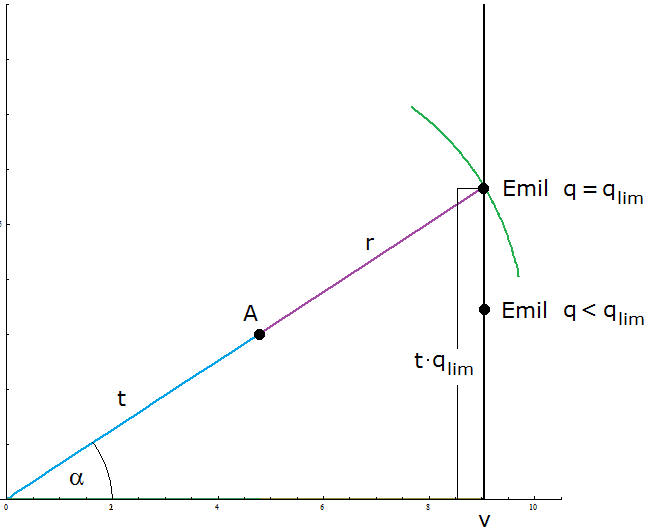Dann ist \[(t+r)^2 = v^2 + t^2~q^2\] Die Lösungen für t sind: \[(1)~~~~t = \frac{r \pm \sqrt{q^2~r^2 + v^2 - q^2~v^2}}{q^2-1}\] Hauptskizze

Bild 6   Hier ist der Grenzfall festgehalten, in dem Emil mit der maximalen Geschwindigkeit läuft, die noch zu seiner Ergreifung führt, und der Wächter den optimalen Winkel \(~\alpha~\) gewählt hat.  –  Die Skizze gilt aber auch für jedes kleinere \(~q~\),  wenn \(~\alpha~\) und \(~t~\) entsprechend angepasst werden.

(1) ist die zentrale Formel für unser Problem. Damit können wir feststellen, für welche Parameter \(~q,~v~\) Lösungen existieren. Wenn wir \(~r~\) und \(~v~\) festhalten, können wir \(~q_{~\text{lim}}~\) berechnen, woraus dann die Strategie des Wächters folgen wird. Wir können aber auch bei gegebenen \(~r~\) und \(~q~\) die maximale Breite \(~v_{~\text{lim}}~\) berechnen; das wird weiter unten noch ausgeführt.

Für \(~q_{~\text{lim}}~\) formen wir (1) wie folgt um: \[(2)~~~~t = \frac{r \pm \sqrt{v^2 - q^2~(v^2-r^2)}}{q^2-1}\] (2) hat nur dann eine reelle Lösung \(~t~\),  falls \(~q^2~\le~v^2/~(v^2-r^2)~\) ist.

Dickpunkt   \(q_{~\text{lim}}~=~v/\sqrt{v^2-r^2}~\).  Nur wenn Emil schneller läuft, wird er entkommen.

Damit ergibt sich die optimale Strategie des Wächters. Wir setzen \(q_{~\text{lim}}~\) für \(~q~\) in (2) ein und erhalten das zugehörige \(~t~\).  Mit \(~t~\) erfolgt dann die Berechnung von \(~\alpha~\).

Dickpunkt   Der Wächter muss maximal die Strecke \(~t = r/~(q^2-1)~\) laufen. Wenn er Emil dann noch nicht gesehen hat, kann er die Verfolgung aufgeben.

Dickpunkt   Die eigentliche Strategie des Wächters ist die Wahl des Startwinkels. Er muss \(~\alpha = \text{arctan}~q~t/v~\) wählen, um Emil zu stellen, wenn dessen Geschwindigkeit höchstens das \(~q_{~\text{lim}}-\)fache der Geschwindigkeit des Wächters beträgt.

Beispiel \[v=9~~~~~~r=5\] \[~~~~~q_{~\text{lim}}=1,2027\] \[~~~~~t=11,2\] \[~~~~~\alpha=56,25°\]


Eine naheliegende Vermutung ist: Wenn Emil mit \(~q \lt q_{~\text{lim}}~\) läuft, hat der Wächter einen gewissen Spielraum bei der Wahl des Winkels \(~\alpha~\).  Dieser Vermutung wollen wir nachgehen, auch wenn es dem Wächter bei seiner Strategie nicht hilft (es sei denn, er weiß, wie schnell Emil läuft). In Bild 7 ist der Zeitpunkt festgehalten, zu dem der Lichtschein Emil erreicht. Dort ist \[x_A = t~\text{cos}~\alpha~~~~~~y_A = t~\text{sin}~\alpha\] \[AD~=~v - x_A~~~~~~DB~=~q~t - y_A\] Mit Pythagoras erhält man damit eine Gleichung für \(~\alpha~\): \[r^2 = (v-x_A)^2 + (q~t-y_A)^2\] Diese Gleichung lösen wir für \(~t~\): \[t~=~\frac{v~\text{cos}~\alpha \pm \sqrt{v^2~\text{cos}^2~\alpha~-~(v^2-r^2)~(1+q^2-2~q~\text{sin}~\alpha)}}{1+q^2-2~q~\text{sin}~\alpha}\] Lösungen gibt es nur, falls der Ausdruck unter der Wurzel nicht negativ ist. Mit \(~z = \text{sin}~\alpha~\) suchen wir deshalb die Nullstellen von \[v^2~(1-z^2)-(v^2-r^2)~(1+q^2-2~q~z)\] Diese Nullstellen (falls sie existieren) sind \[z_{1,2}~=~\frac{q~(v^2-r^2)~\pm~r \cdot \sqrt{v^2-q^2~(v^2-r^2)}}{v^2}\] Die möglichen \(~\alpha~\) in Bild 7 liegen dann zwischen \(~\text{arcsin}~z_1~\) und \(~\text{arcsin}~z_2~\).

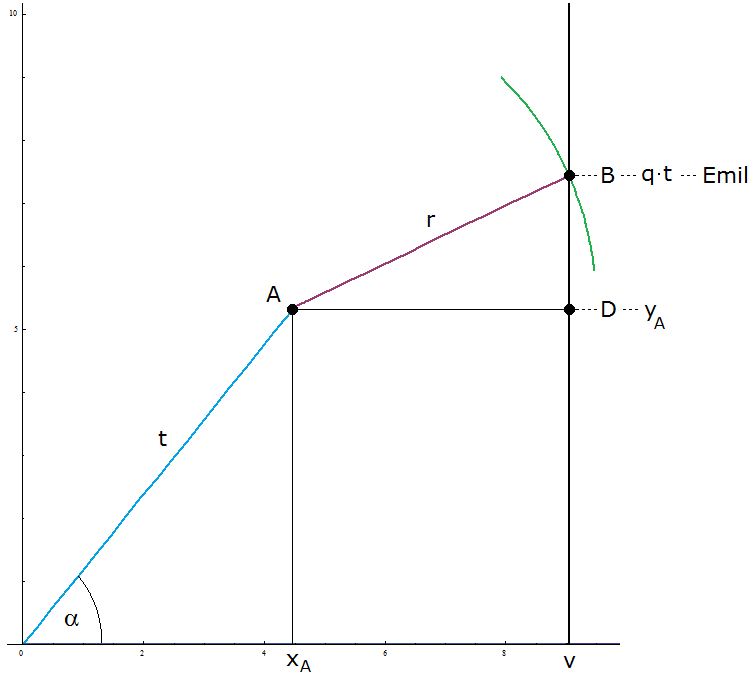
q < qlim

Bild 7   Emil läuft mit \(~q \lt q_{~\text{lim}}\)

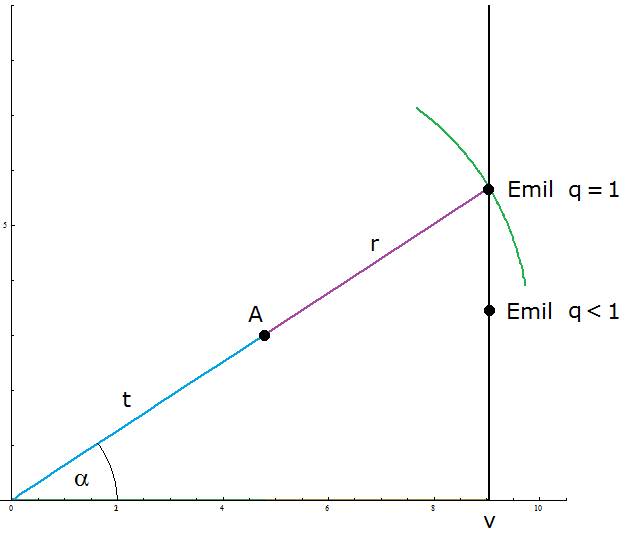
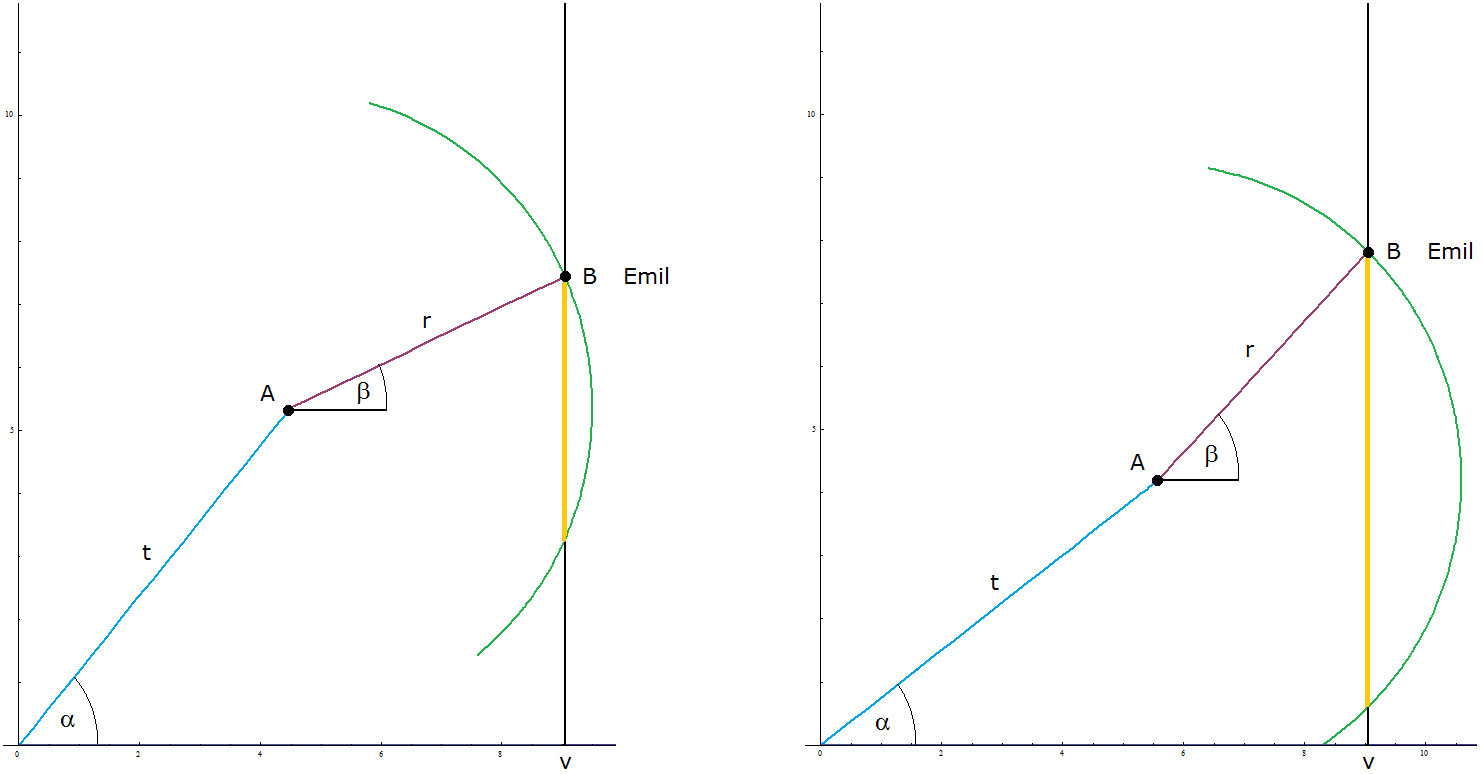
Beispiel \[v=9~~~~~~r=5~~~~~~q=1,17\] \[~~~~~\alpha \in [~42,86°,~69,64°]\]


Wie oben schon erwähnt, ist (1) eine universelle Formel für Berechnungen zum Szenario "Emil auf der Flucht  –  Wächter mit Laterne". Nehmen wir an, dass Emil den Radius \(~r~\) der Laterne und die Laufgeschwindigkeit des Wächters kennt oder abschätzen kann. Dann ermöglicht (1) ihm zu berechnen, wie breit der Gang sein muss, damit er sicher entkommen kann. Denn auch für diese Konstellation lässt sich Bild 5 heranziehen: \(~v~\) kann nicht die Grenzbreite des halben Ganges sein, da der rechte Rand des Gangs auch durch \(~B~'~\) verlaufen könnte und Emil dennoch gefasst würde. Die Folgerung \(~\alpha = \beta~\) gilt also auch hier.  –  Wir formen (1) um: \[(3)~~~~t = \frac{r \pm \sqrt{q^2~r^2 - v^2~(q^2-1)}}{q^2-1}\] (3) hat nur dann eine reelle Lösung \(~t~\),  falls \(~v^2~\le~q^2~r^2~/~(q^2-1)~\) ist.

Dickpunkt    \(v_{~\text{lim}}~=~q~r~/~\sqrt{q^2-1}~\) ist die Grenzbreite des halben Gangs, bei der der Wächter eine Chance hat, Emil zu stellen.

Beispiel \[r=5~~~~~~q=1,2\] \[~~~~~v_{~\text{lim}}~=~9,0453\]


Quellen

[1]  The Riddler Classic 2022-05-27

[2]  The Riddler Classic Solution 2022-06-03



Kommentare sind willkommen.


Stand 2023-08-02

Inhalt Blog   |    voriger Eintrag   |    nächster Eintrag

Manfred Börgens   |   Zur Leitseite