Dodekaeder    MB Matheblog # 30 Inhalt Blog
voriger Eintrag    nächster Eintrag		 zur Leitseite
Index der gesamten Website


2023-11-20


Emil auf der Flucht  –  Teil 2                    Kommentare sind willkommen.


Als Gastautor hat   Kevin Börgens, Chicago  wieder die wesentlichen Teile dieses Beitrags erarbeitet.

Das Szenario ist weitgehend wie in Teil 1 und wird hier nicht in allen Einzelheiten wiederholt. Wieder läuft Emil auf dem Weg in die Freiheit durch einen langen dunklen Gang. In diesem wartet ein Wächter auf ihn, der ihn aber nur erkennen kann, wenn Emil in den Lichtschein seiner Laterne gerät. Der Durchmesser des Lichtscheins der Laterne ist kleiner als die Breite des Gangs. Er kann Emils Schritte nicht hören, weil dieser auf Gummisohlen läuft. Der Wächter läuft deshalb immer hin und her (oder schwenkt seine Laterne), so dass der Lichtschein abwechselnd auf eine der beiden Wände fällt.

Wir wollen die Situation von Emil und dem Wächter mathematisch formulieren:
Wir wollen überlegen, wie sich Emil bewegen sollte, um zu entkommen (falls das überhaupt möglich ist), und wie sich der Wächter bewegen sollte, um dies zu verhindern. Das führt auf eine Reihe von Fragestellungen (in grüner Schrift), und bei jeder sollten die Leser erst mal nicht weiterlesen, sondern selbst versuchen die Antwort herauszufinden.


Dickpunkt   Wie sollte Emil im Gang laufen, um seine Chancen auf das Entkommen zu maximieren ?

Bild 1 zeigt, wie sich der Lichtschein auf Höhe der Laterne im Gang bewegt. Der Wächter befindet sich im Mittelpunkt des Kreises, also im Intervall \(~[-a,~a]~\) auf der "Wächterlinie" (Pfeil neben der linken Skizze). Der Nullpunkt der Wächterlinie wurde in die Gangmitte gelegt. In grün und orange wurden beispielhaft zwei Sehnen der Länge \(~2\cdot s~\) eingezeichnet, die sich mit dem Kreis parallel zur Wächterlinie bewegen; es kann auch \(~s=r~\) sein.

Emil kann sich irgendwo im Gang aufhalten; aus Symmetriegründen wollen wir uns dabei auf die rechte Ganghälfte beschränken. Sein Abstand zur Nulllinie soll \(~x~\) betragen, mit \(~x\in [~0,~v~]~\);  in Bild 1 befindet er sich also auf der Geraden \(~E~\).  –  Für die Bewegung des Wächters reicht es, ebenfalls aus Symmetriegründen, einen vollständigen Lauf von links nach rechts zu betrachten, also mit Start in \(~-a~\) und mit Ende in \(~a~\).

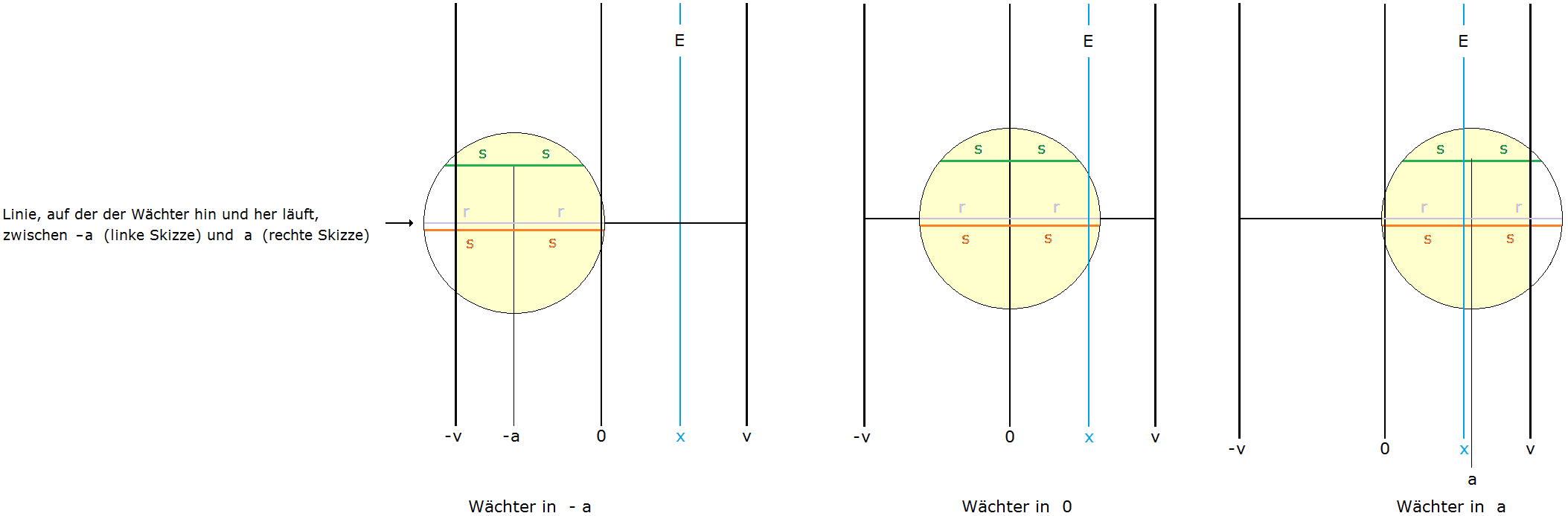
Lichtkreise

Bild 1  Die Schnittebene des Gangs in Höhe der Laterne wird von dieser kreisförmig oder kreissegmentförmig beleuchtet. Falls sich Emil auf der Geraden \(~E~\) aufhält, ist es dort zu einem bestimmten Zeitanteil hell.

Emils Ziel ist es, dem Lichtschein zu entgehen. Die Berechnung der Zeitdauer \(~d(x)~\),  in der die Sehne die Gerade \(~E~\) überlappt, soll ihm dabei helfen. Eine naheliegende Vermutung ist, dass es an der Wand  (\(~x=v~\))  die längste Dunkelphase gibt.

Die orangene Sehne in Bild 1 steht für den Fall, dass \(~s\ge a~\) ist, d.h. die Sehne überlappt die Nulllinie immer. Für \(~x\le s-a~\) ist dann \(~E~\) immer beleuchtet. Also können wir \(~x~\) weiter einschränken: \[x\in [~\text{max}~\{~s-a,~0~\},~v~]\] Wir stellen uns nun vor, dass der Lichtkreis in Bild 1 von links nach rechts verschoben wird. Die Sehne der Länge \(~2\cdot s~\) erreicht \(~E~\),  wenn sich der Wächter in \(~x-s~\) befindet. Wir beschreiben die Phase, in der \(~E~\) beleuchtet ist:

Position Wächter im Intervall  \([~x-s,~\text{min}~\{~x+s,~a~\}~]~~~~\Longrightarrow~~~~d(x) = \text{min}~\{~2\cdot s,~s+a-x~\}\)

Wegen \(~a-v \le 0~\) gilt für \(~x=v~\): \[d(v) = \text{min}~\{~2\cdot s,~s+a-v~\}~=~s+a-v~\le~d(x)\] Die Vermutung hat sich also als zutreffend erwiesen. Zu einem zufällig gewählten Zeitpunkt ist ein zufällig gewählter Punkt an der Wand für Emil günstiger als ein Punkt weiter links.

Es wird unterstellt, dass sich Emil rational verhält (der Wächter natürlich auch; darauf kommen wir noch zu sprechen). Ab hier gehen wir davon aus, dass Emil an der rechten Wand entlangläuft.

Die nächste graphische Darstellung in Bild 2 soll einen Überblick über die Bewegung des Wächters und des Lichtscheins geben. Sie zeigt, wie sich der Lichtschein an den Wänden des Gangs verändert. Die Darstellung wird weiter unter mehrfach aufgegriffen und soll erklärt werden:

Die senkrechten Linien stellen jeweils das selbe Stück der Gangwand im Bereich des Wächters dar, und zwar von links nach rechts zu verschiedenen Zeitpunkten. Gelb gefärbt sind für jeden senkrechten Schnitt die Wandbereiche, die im Licht liegen.

Für die Interpretation von Bild 2 schauen wir uns zuerst den "Kernbereich" \(~z_9~-~z_{11}~\) an. Zum Zeitpunkt \(~z_9~\) ist der Wächter in der Gangmitte, auf dem Weg von der linken Wand zur rechten Wand; beide Wände sind unbeleuchtet. Dies wurde als Nullpunkt für die Zeit \(~z~\) und die Position des Wächters gewählt. Der Wächter bewegt sich dann nach rechts; zum Zeitpunkt \(~z_{10}~\) mit \(~z=v-r~\) erreicht der Lichtschein die rechte Wand. Der Wächter läuft weiter bis \(~a~\);  dies ist sein Umkehrpunkt, bei dem die rechte Wand maximal beleuchtet wird. Auf diese Weise sind auch die anderen Zeitpunkte in Bild 2 zu lesen; die "Vorgeschichte" mit negativen Zeitpunkten geht zurück bis zur kompletten vorherigen beleuchteten Phase der rechten Wand. Zu den Zeitpunkten \(~z_5~-~z_7~\) ist die linke Wand beleuchtet.

Die schräge Gerade stellt ein Beispiel für Emils Lauf dar; ihre Steigung \(~q~\) entspricht seiner Geschwindigkeit. Emils Laufweg ist in der Skizze rein zufällig gewählt. Emil quert die Wächterlinie zum Zeitpunkt \(~z_8~\), also noch bevor der Wächter die Gangmitte erreicht hat. Ab dem Zeitpunkt \(~z_{10}~\) läuft er vor dem Lichtschein her, der ihn aber schließlich einholt.

Erlaeuterung

Bild 2

Die Darstellung in Bild 2 findet sich im Wesentlichen auch in Bild 3 wieder. Dort wird gezeigt, dass es einen Idealweg für Emil gibt, der aus Sicht des Wächters am ungünstigsten verläuft.

Emil quert die Wächterlinie zu drei verschiedenen Zeitpunkten, mit einer Geschwindigkeit, die ihn (wenn er Glück hat) entkommen lässt . Nur in der linken Skizze wird er gefasst. Die beiden rechten Skizzen zeigen: Falls er (irgendwie) entkommen kann, dann kann er auch entkommen, wenn er sich symmetrisch zu den hellen Phasen an seiner Wand bewegt; er quert dann die Wächterlinie, wenn der Wächter sich maximal weit nach links bewegt hat, also würde in Bild 2 der Zeitpunkt \(~z_8~\) auf dem Zeitpunkt \(~z_6~\) liegen (rechte Skizze in Bild 3). Diese symmetrische Lage von Emils Laufweg ist deshalb optimal für ihn. Allerdings weiß Emil im Normalfall nicht, wie er diesen Laufweg nehmen soll, denn er kennt die Parameter \(~r,~a~\) und \(~q~\) nicht.

Emil-Wege

Bild 3   \(v = 5,5~~~~~~r = 5~~~~~~a = 0,9~~~~~~q = 1,2\)
Emil quert die Wächterlinie zu drei verschiedenen Zeitpunkten.

Nun wollen wir eine Frage behandeln, die sowohl für Emil als auch für den Wächter von Interesse ist.


Dickpunkt   Wie breit muss der Gang mindestens sein, damit Emil eine Chance hat zu entkommen ?

Diese Frage unterstellt, dass es  erstens  Gangbreiten gibt, die es dem Wächter in jedem Fall erlauben, Emil zu stellen, und dass  zweitens  diese Gangbreiten ein Maximum haben, und dass  drittens  Emil bei breiteren Gängen nur vielleicht, d.h. mit positiver Wahrscheinlichkeit, entkommen kann. Wir werden noch sehen, dass die ersten beiden Unterstellungen berechtigt sind, die letzte aber genauer formuliert werden muss.

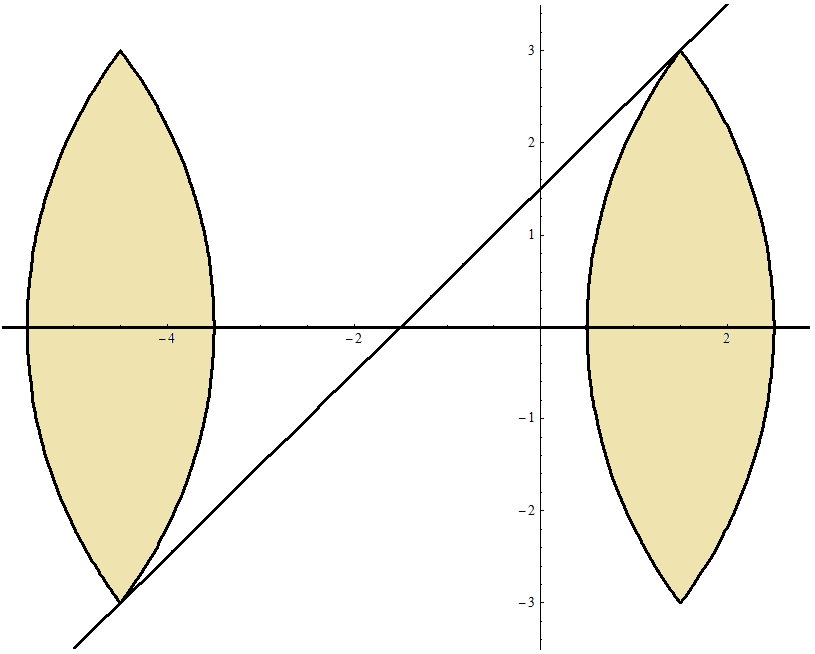
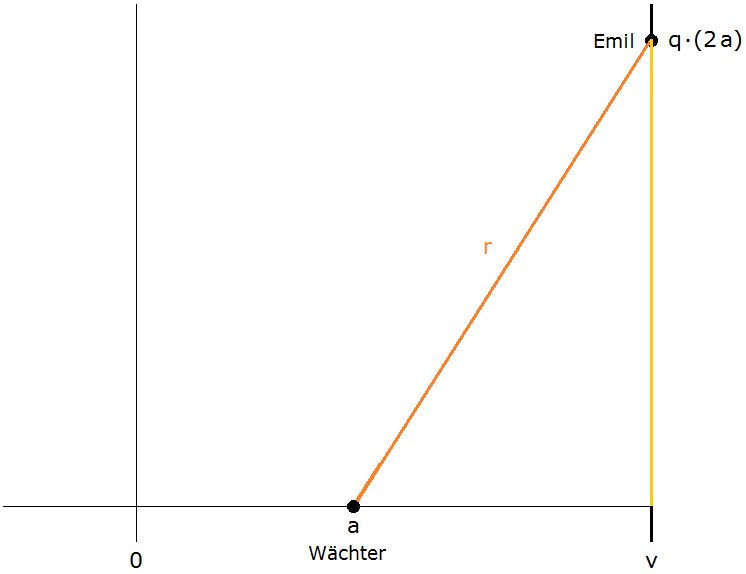
Die Überlegungen zu Bild 3 zeigen, dass Bild 4 den Grenzfall darstellt: Der Lichtschein erreicht Emil nur punktuell und nicht in einem Zeitintervall. Jede Parallelverschiebung der Geraden würde zur sicheren Ergreifung von Emil führen.

Grenzfall

Bild 4  Grenzfall (vgl. mit Bild 3)    \(v = 5,5~~~~~~r = 5~~~~~~a = 1,5~~~~~~q = 1\)

Für die weiteren Rechnungen wählen wir die Darstellung in Bild 5, harmonierend mit den Bildern 4 und 2 (Zeitpunkt \(~z_{11}~\)). Wir sehen die gleiche Ansicht des Gangs wie in Bild 1. Wenn Emil das obere Ende des Dreicks erreicht, hat der Wächter den Weg von \(~-a~\) bis \(~a~\) zurückgelegt. Der Wächter benötigt dafür \(~2~a~\) und Emil \(~2~q~a~\) Zeiteinheiten.

Grenzfall

Bild 5  Grenzfall wie in Bild 4

Aus der Gleichung \[r^2 = (v-a)^2~+~4~q^2~a^2\] folgt \[v = a + \sqrt{r^2~-~4~a^2~q^2}\] Eine kleine Rechnung ergibt, dass \(~v~\) genau ein Maximum hat: \[v_{max} = \frac{r}{2~q} \sqrt{4~q^2+1}~~~~~\text{bei}~~~~~a = \frac{r}{2~q~\sqrt{4~q^2+1}}\] Wir können also nicht nur die Gangbreite für den Grenzfall ausrechnen, sondern auch, welche Strategie der Wächter einschlagen muss, denn seine Auslenkung \(~a~\) von \(~0~\) wird mitgeliefert. Das ist natürlich nur dann hilfreich für ihn, wenn er über \(~q~\) informiert ist.

Beispiel \[r=5~~~~~~q=1,2\] \[~~~~~v_{~\text{max}}~=~5,4167\] \[~~~~~a~=~0,8013\]



Dickpunkt   Die Wächter-Strategie

Gegenüber der vorigen Aufgabe sollen nun die Rollen von \(~v~\) und \(~q~\) getauscht werden. Der Wächter kennt also die halbe Gangbreite \(~v~\).  Wie schnell darf Emil laufen, damit der Wächter ihn sicher erwischen kann? Das läuft auf die Bestimmung eines \(~q_{max}~\) hinaus. Wir werden sehen, dass dies genügt, um eine optimale Strategie für den Wächter anzugeben, die für alle \(~q \le q_{max}~\) erfolgreich ist.

Bild 5 ergab die Gleichung \(~r^2 = (v-a)^2~+~4~q^2~a^2\),  die jetzt nach \(~q~\) aufgelöst wird: \[q = \frac{\sqrt{r^2-(v-a)^2}}{2~a}\] Eine kleine Rechnung ergibt, dass \(~q~\) genau ein Maximum hat: \[q_{max} = \frac{r}{2~\sqrt{v^2-r^2}}~~~~~\text{bei}~~~~~a = \frac{v^2-r^2}{v}\] Wir können also nicht nur die Grenzgeschwindigkeit ausrechnen, sondern auch, welche Strategie der Wächter einschlagen muss, denn seine Auslenkung \(~a~\) von \(~0~\) wird mitgeliefert.

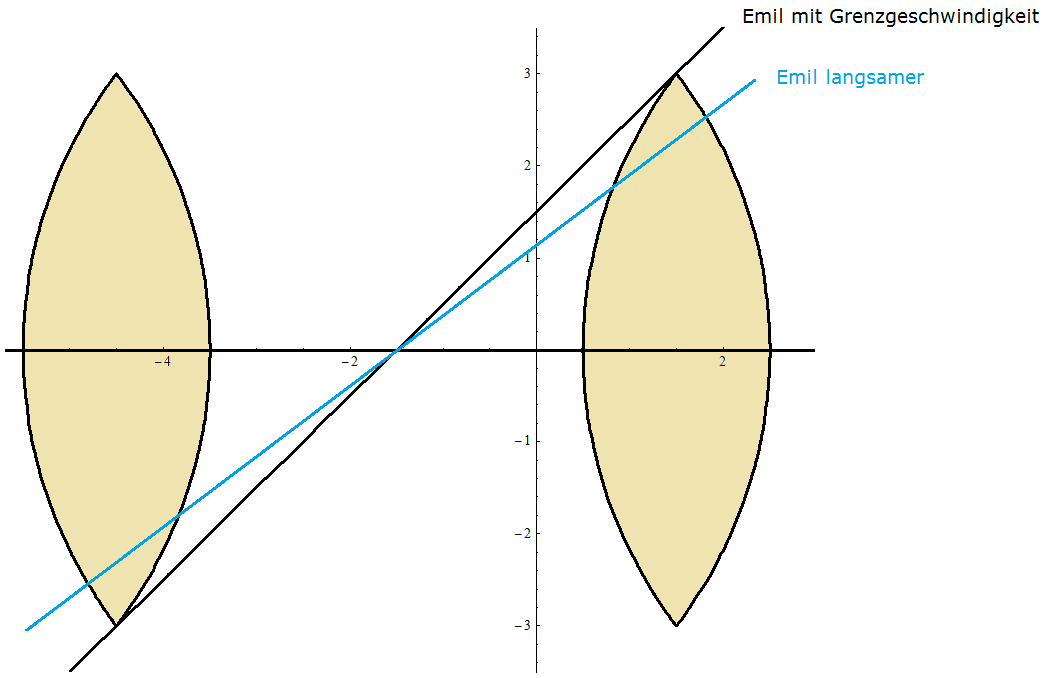
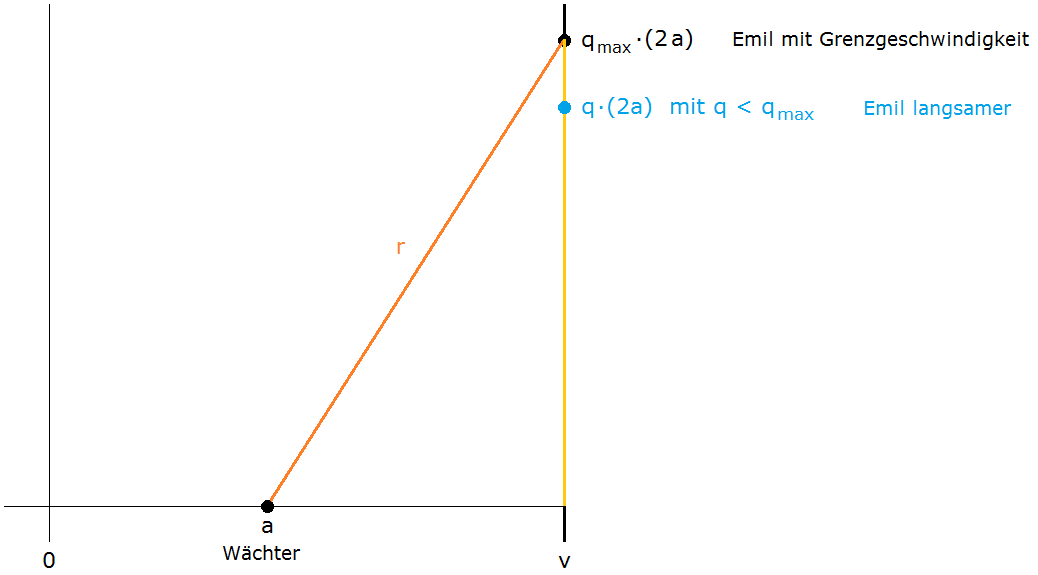
Diese Strategie ist auch für alle kleineren \(~q~\) erfolgreich, wie das folgende Bild 6 zeigt, das die Bilder 4 und 5 modifiziert. Kleinere Geschwindigkeiten bedeuten in Bild 4 kleinere Steigungen der Geraden und in Bild 5 einen Ort für Emil, der unterhalb seiner Position mit Grenzgeschwindigkeit liegt. Für \(~q \lt q_{max}~\) muss der also der Wächter seine Strategie nicht ändern.

modifiziert    modifiziert

Bild 6   Bilder 4 und 5 modifiziert

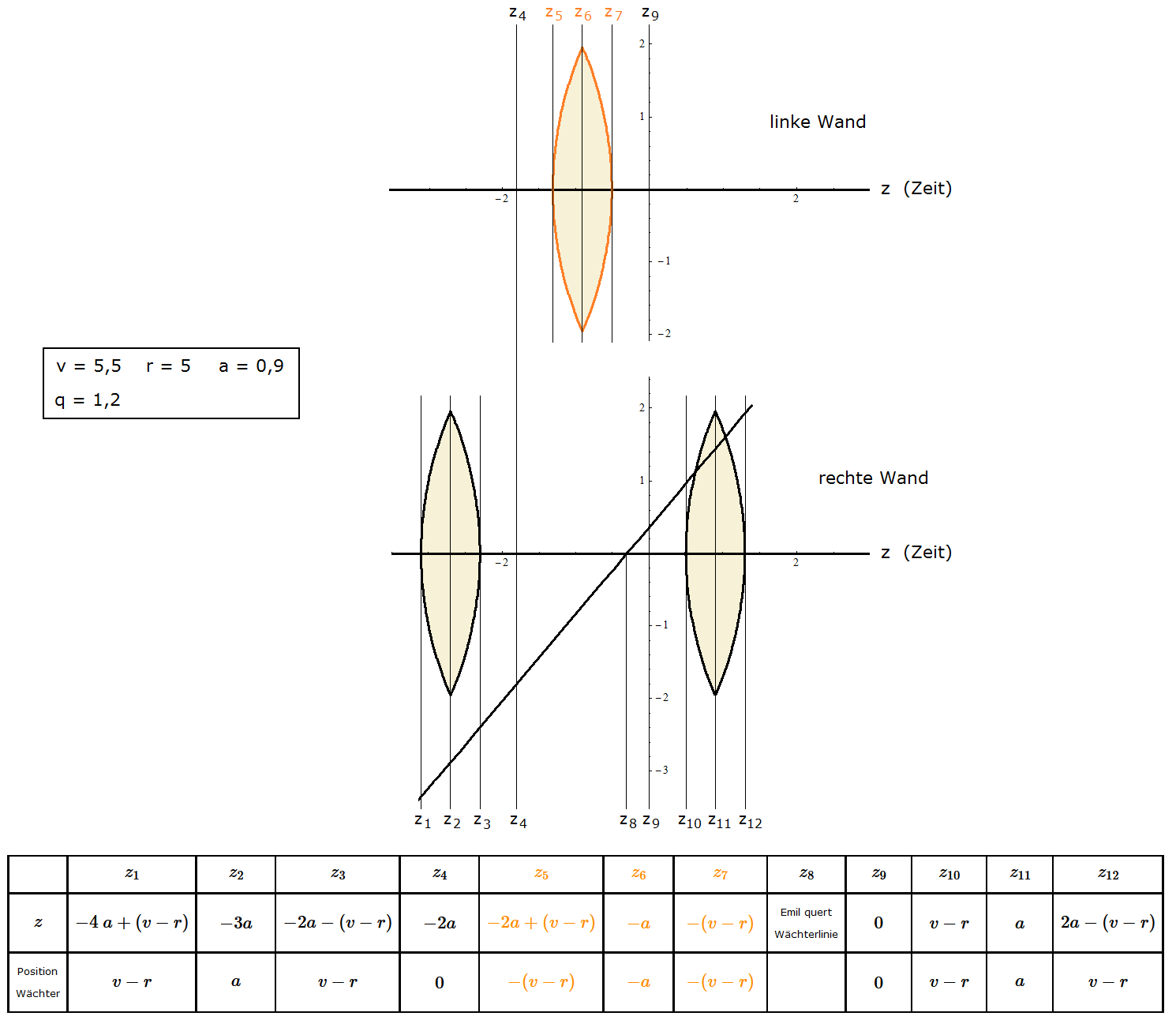
Beispiel \[v=5,5~~~~~~r=5\] \[~~~~~q_{~\text{max}}~=~1,0911\] \[~~~~~a~=~0,9545\]



Dickpunkt   Intervall für \(~a\)

Bild 7 zeigt bei konstanten Parametern \(~v,~r,~q~\) drei verschiedene Strategien des Wächters. In allen drei Skizzen läuft Emil den symmetrischen Optimalweg. Links bewegt sich der Wächter nur wenig, und Emil hat die Möglichkeit zu entkommen. Rechts läuft der Wächter bis fast zu den Wänden, und Emil hat ebenfalls die Möglichkeit zu entkommen. Die mittlere Skizze zeigt eine Bewegung des Wächters, die sicher zur Ergreifung Emils führt. Die Vermutung liegt nahe, dass es im Fall einer möglichen Ergreifung Emils ein Intervall für \(~a~\) gibt, in dem die Ergreifung sicher ist; für \(~a~\) außerhalb dieses Intervalls kann Emil entkommen, falls er einen günstigen Laufweg nimmt.

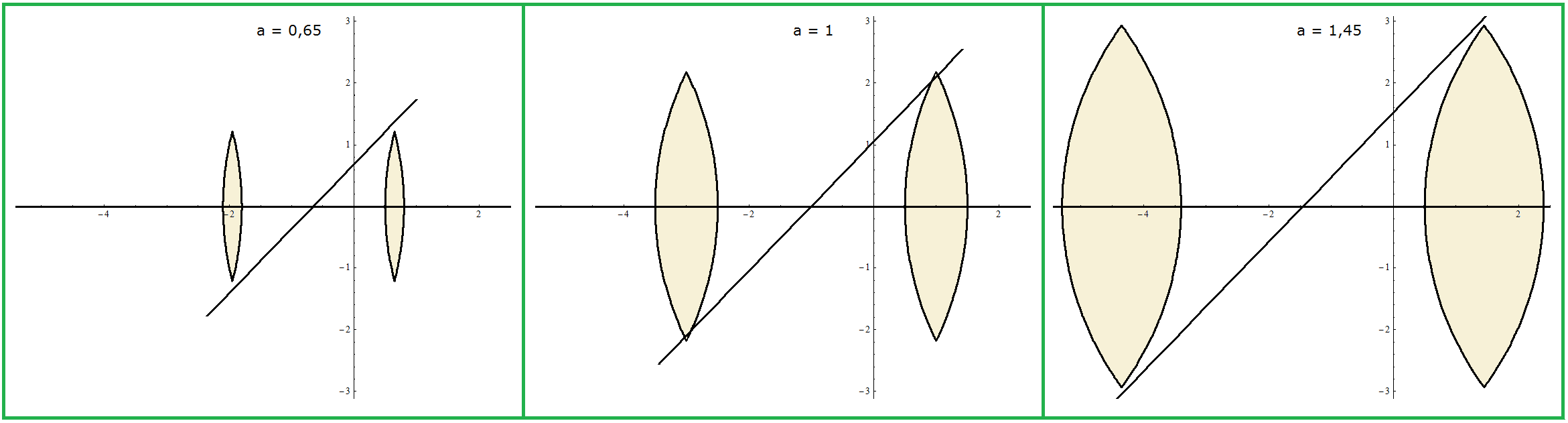
verschiedene a

Bild 7   \(v = 5,5~~~~~r=5~~~~~q=1,05\)

Wir schauen uns die rechte Skizze von Bild 6 an: \[4~q^2~a^2~\le~4~q_{max}^2~a^2~=~r^2-(v-a)^2\] \[\Longrightarrow\] \[a \in \left[~\frac{v-\sqrt{r^2-4~q^2~(v^2-r^2)}}{4~q^2+1},~\frac{v+\sqrt{r^2-4~q^2~(v^2-r^2)}}{4~q^2+1}~\right]\] Der Wächter kennt allerdings diesen Spielraum nur, wenn er über \(~q~\) informiert ist.

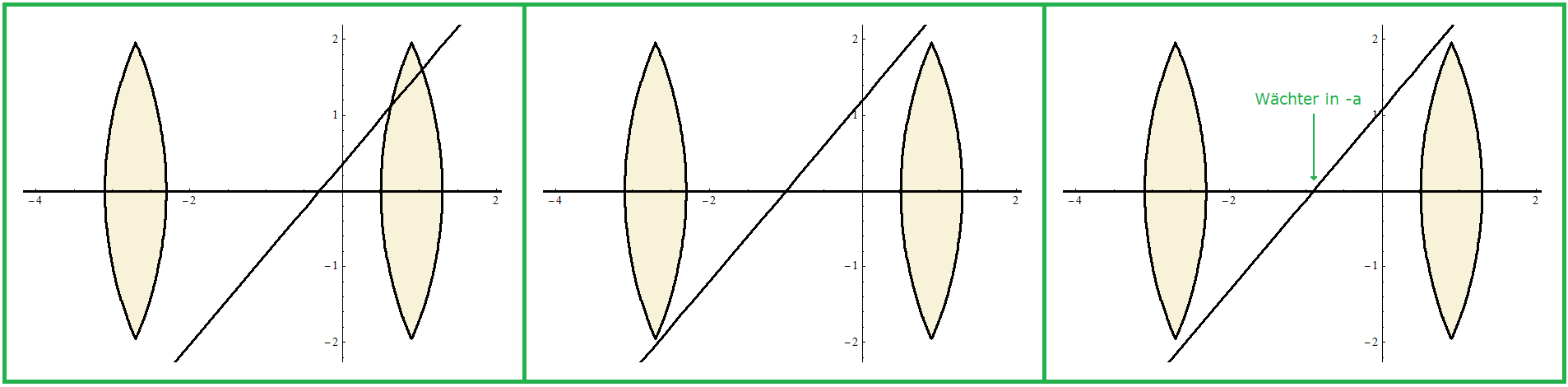
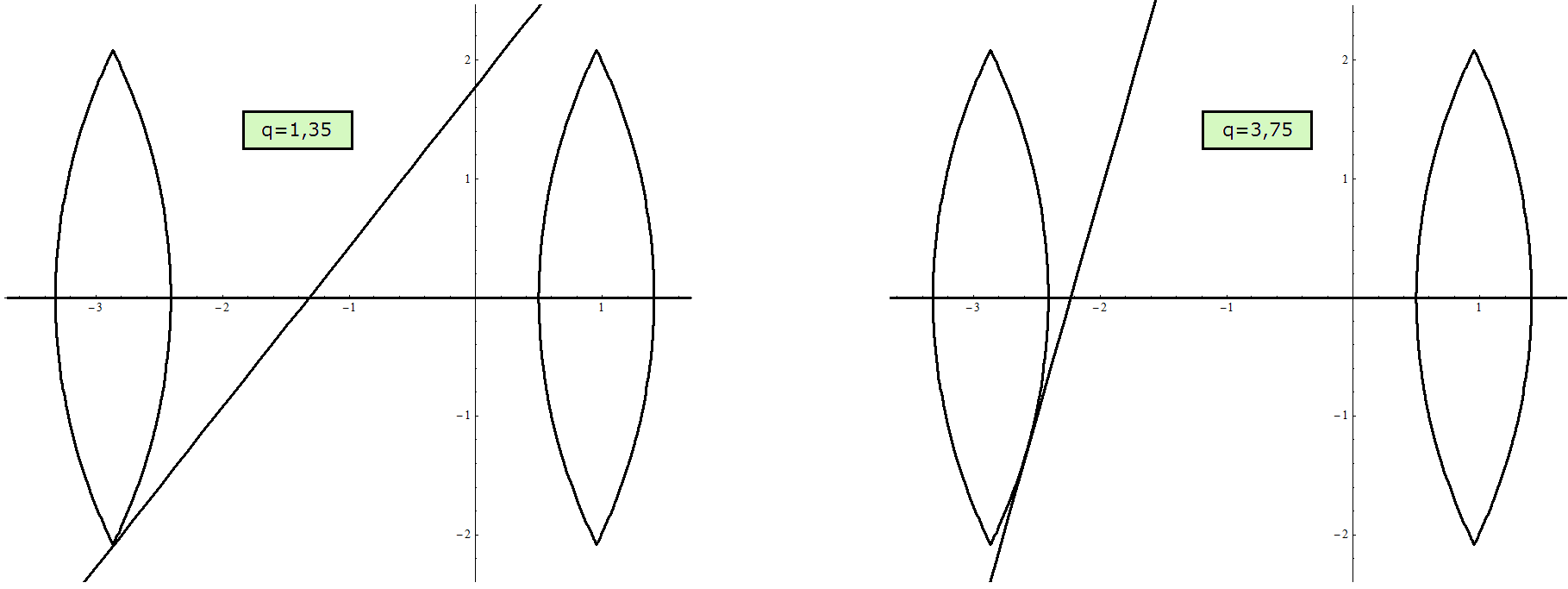
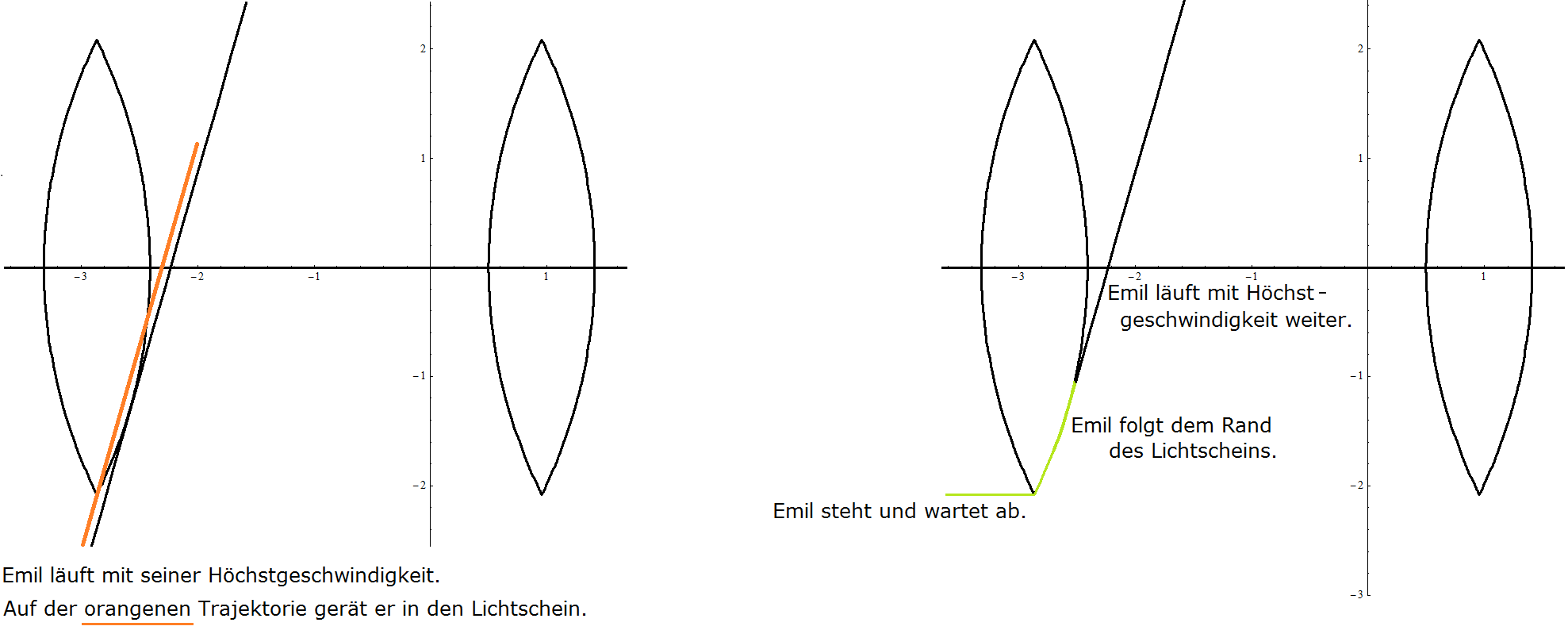
Beispiel  (vgl. Bild 7) \[v=5,5~~~~~~r=5~~~~~~q=1,05\] \[~~~~~a \in [~0,7654~,~~1,2679~]\]


Dickpunkt   Emils Strategie

Es war noch nicht die Rede davon, dass Emil seine Chance zum Entkommen beeinflussen könnte. In der Tat mag es scheinen, dass er entweder vom Wächter sicher gestellt wird (falls er zu langsam läuft), oder dass er zufällig entkommt, so wie das in Bild 3 dargestellt wurde. Aber Bild 3 gibt den Hinweis, dass es für die Überquerung der Wächterlinie (\(~z_8~\) in Bild 2) Zeitintervalle gibt, die günstig für Emil sind. Diese Intervalle entsprechen denjenigen Parallelverschiebungen der Geraden in Bild 3, die nicht durch die beleuchteten Areale verlaufen. Es muss also nicht die "Ideallinie" sein (in Bild 3 rechts), denn diese wurde für den Grenzfall berechnet (Bild 4). Insbesondere könnte die Gerade so verlaufen, dass sie die linke beleuchtete Fläche tangiert. Bild 8 zeigt, wie das aussehen könnte:

Verhalten von Emil

Bild 8   \(v = 5,5~~~~~r=5~~~~~a=0,9545~\)  (wie im Beispiel unter Bild 6)

Emil kann sehr wohl etwas für sein Entkommen tun. Versetzen wir uns in Emil hinein. Er läuft den Gang entlang (an der Wand). Irgendwann sieht er einen Lichtschein. Wenn er vernünftig ist, wird er vorsichtig sein und nicht einfach mit seiner Höchstgeschwindigkeit weiterrennen (Vorsicht: Für Emils Höchstgeschwindigkeit steht \(~q~\), nicht \(~q_{max}~\)).  Bei Annäherung an den Wächter beobachtet er, dass an der Wand ein Lichtschein in regelmäßigen Abständen erscheint, dann größer wird, dann wieder kleiner, und dann für eine kurze Zeit verschwindet. Schauen wir uns nun die linke Skizze in Bild 8 an. Sobald Emil die Regelmäßigkeit des Lichtscheins verstanden hat, stellt er sich ganz kurz vor den Punkt der maximalen Lichtausdehnung und läuft los, sobald der Lichtschein kleiner wird. Das sichert ihm in diesem Beispiel das Entkommen, falls er schneller läuft als mit der \(q_{max}-\)fachen Geschwindigkeit des Wächters.

Nun könnte es allerdings sein, dass Emil so schnell laufen kann, dass er mit der eben dargestellten Strategie in den Lichtschein gerät. Die rechte Skizze in Bild 8 zeigt so einen Fall. Er wird links in Bild 9 verdeutlicht. Die rechte Skizze zeigt, wie sich Emil verhalten sollte: Er läuft los, sobald der Lichtschein zurückgeht, aber nur so schnell, das er dem Rand des Lichtscheins folgt, ohne hinein zu geraten.

Verhalten von Emil

Bild 9    Die Parameter sind die gleichen wie in Bild 8 rechts:  \(v = 5,5~~~~~r=5~~~~~a=0,9545~~~~~q=3,75\)

Emils Strategie lässt sich so zusammenfassen: Durch Beobachtung des Lichts an der Wand passt er den Zeitpunkt ab, zu dem der Lichtschein dort seine maximale Ausdehnung hat. Dann läuft er so schnell wie möglich los, aber er vermeidet, ins Licht zu geraten. Das kann bedeuten, dass er für ein kurzes Stück nicht mit seiner Höchstgeschwindigkeit läuft.


Fazit

Das Szenario, das wir am Anfang beschrieben haben, konnte umfassend mathematisch analysiert werden. Wir nehmen an, dass Emil und der Wächter rational handeln und mathematisch beschlagen sind. Dann gibt es für beide jeweils eine optimale Strategie. Bis zu einer Grenzgeschwindigkeit von Emil wird ihn der Wächter stellen; falls Emil schneller läuft, wird er entkommen.



Kommentare sind willkommen.


Stand 2023-09-03

Inhalt Blog   |    voriger Eintrag   |    nächster Eintrag

Manfred Börgens   |   Zur Leitseite