 MB Matheblog # 27
MB Matheblog # 27voriger Eintrag nächster Eintrag
Index der gesamten Website
 MB Matheblog # 27 MB Matheblog # 27 |
Inhalt Blog voriger Eintrag nächster Eintrag |
zur Leitseite Index der gesamten Website |
|
Unter den Hunderten mathematischer Probleme, denen ich begegnet bin und die ich zum Teil in der Problem-Rubrik auf dieser Website vorgestellt habe, sind einige wenige, die zu meinen klaren Favoriten zählen. Ich mag Probleme, die einen gewissen "Pfiff" haben oder ein "Aha-Erlebnis" beim Leser hervorrufen, und auch solche, die verblüffend oder gar paradox erscheinen. All diese Eigenschaften finden sich in dem Tortenproblem, das hier behandelt werden soll. Unter meinen Favoriten steht es seit längerem an der Spitze (gefolgt vom Mauerschatten-Blog # 3).
Das Tortenproblem hätte auch in der Problem-Rubrik erscheinen können, aber ich habe mich für den Blog entschieden, weil die Lösung nicht ganz einfach ist. Zuerst soll die Ausgangslage des Problems und das einfachste Beispiel beschrieben werden: |
Bild 1 
|
|
Tortenproblem – Einführung
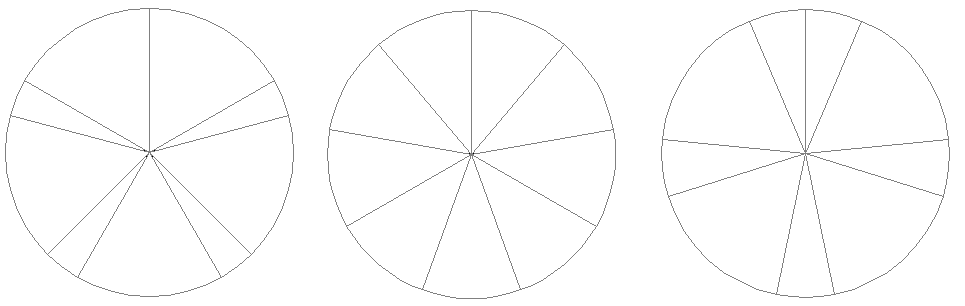
Wir nehmen eine kreisrunde Torte mit einer dunklen Oberfläche (z.B. Schokolade) und einem hellen Boden. Aus ihr werden Tortenstücke gleicher Größe in Form von Kreissektoren ausgeschnitten (siehe Bild 1). Jedes Stück grenzt an seinen Vorgänger und liegt im Gegenuhrzeigersinn neben ihm. Wenn ein Stück ausgeschnitten ist, wird es umgedreht, ändert also seine Farbe (siehe Bild 1). Der Einfachheit halber werden wir nicht immer von Dunkel und Hell, sondern meist von Schwarz und Weiß sprechen. Zur Standardisierung dieses Vorgangs stellen wir uns vor, dass die Schnitte nicht gesetzt werden, indem jemand mit dem Messer um die Torte herumgeht, sondern die Schnitte werden immer am oberen Kreisrand angesetzt und der Kuchen wird im Uhrzeigersinn weitergedreht. Mit Ausnahme des allerersten Schnitts ("Schritt 0", der im Folgenden bedeutungslos ist und nicht mitgezählt wird) soll ein "Schritt" aus drei Aktionen bestehen: - Drehen der Torte um einen Winkel α - Schneiden - Wenden des eben abgeschnittenen Tortenstücks Im einfachsten Fall ist α = 360°/m mit natürlichem m ≥ 2 . Dann lassen sich genau m Stücke ohne Rest aus der Torte schneiden. Für m = 9 zeigen wir mehrere Einzelschritte: 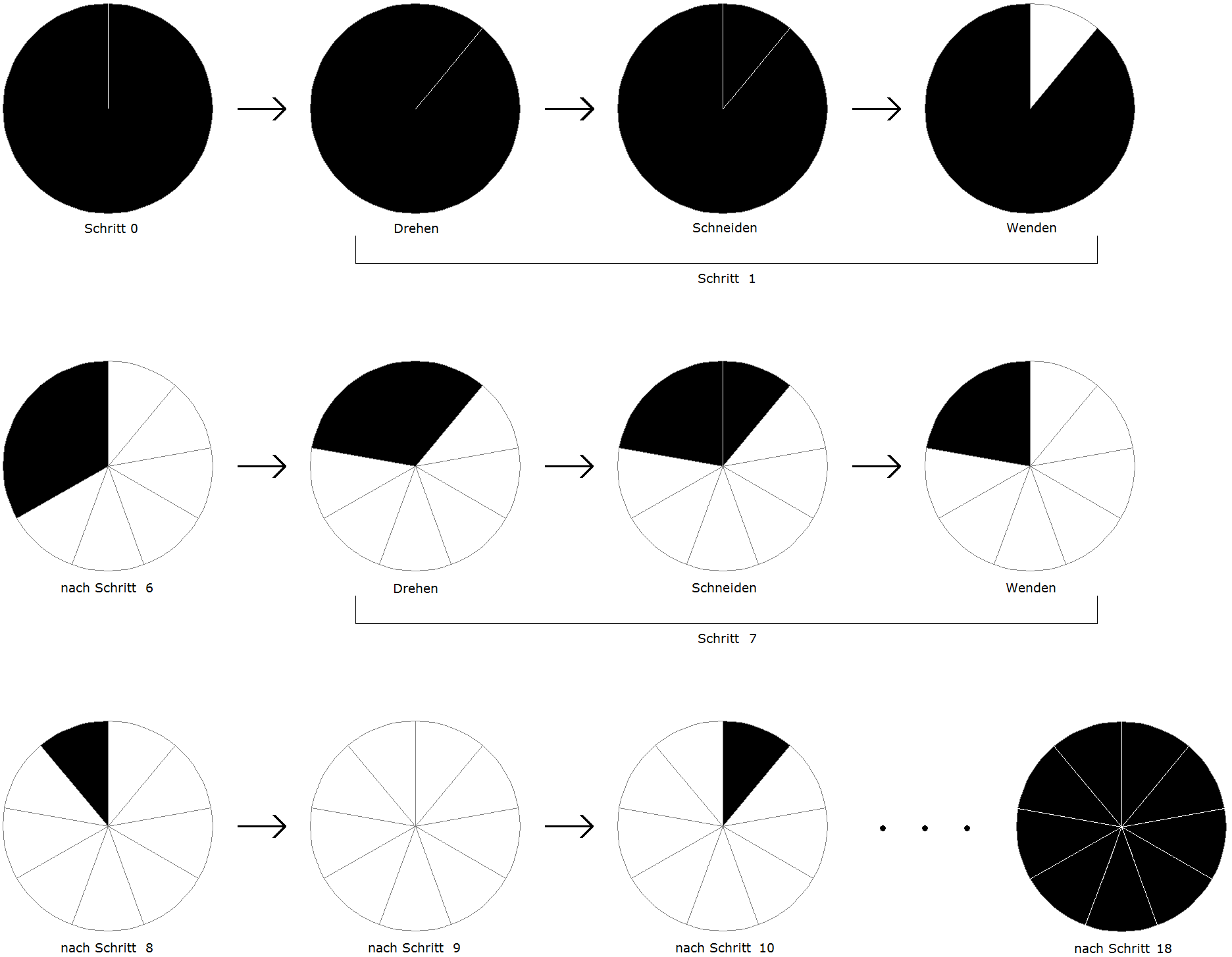
Bild 2 α = 360°/9 = 40° Was in Bild 2 gezeigt wurde, ist im Folgenden für beliebige Winkel α das Ziel: Es soll solange gedreht, geschnitten und gewendet werden, bis die Torte auf der Oberfläche wieder ganz dunkel ist. Für α = 360°/m werden s = 2m Schritte benötigt. Natürlich stellen sich sofort interessante Fragen: Geht das immer? Wieviel Schnitte werden benötigt? |
|
Bei α ≠ 360°/m ist alles anders !
Wir zeigen in Bild 3 oben den "Überlappungs"-Schritt und unten den Folgeschritt sowie einen weiteren, willkürlich herausgegriffenen Schritt. 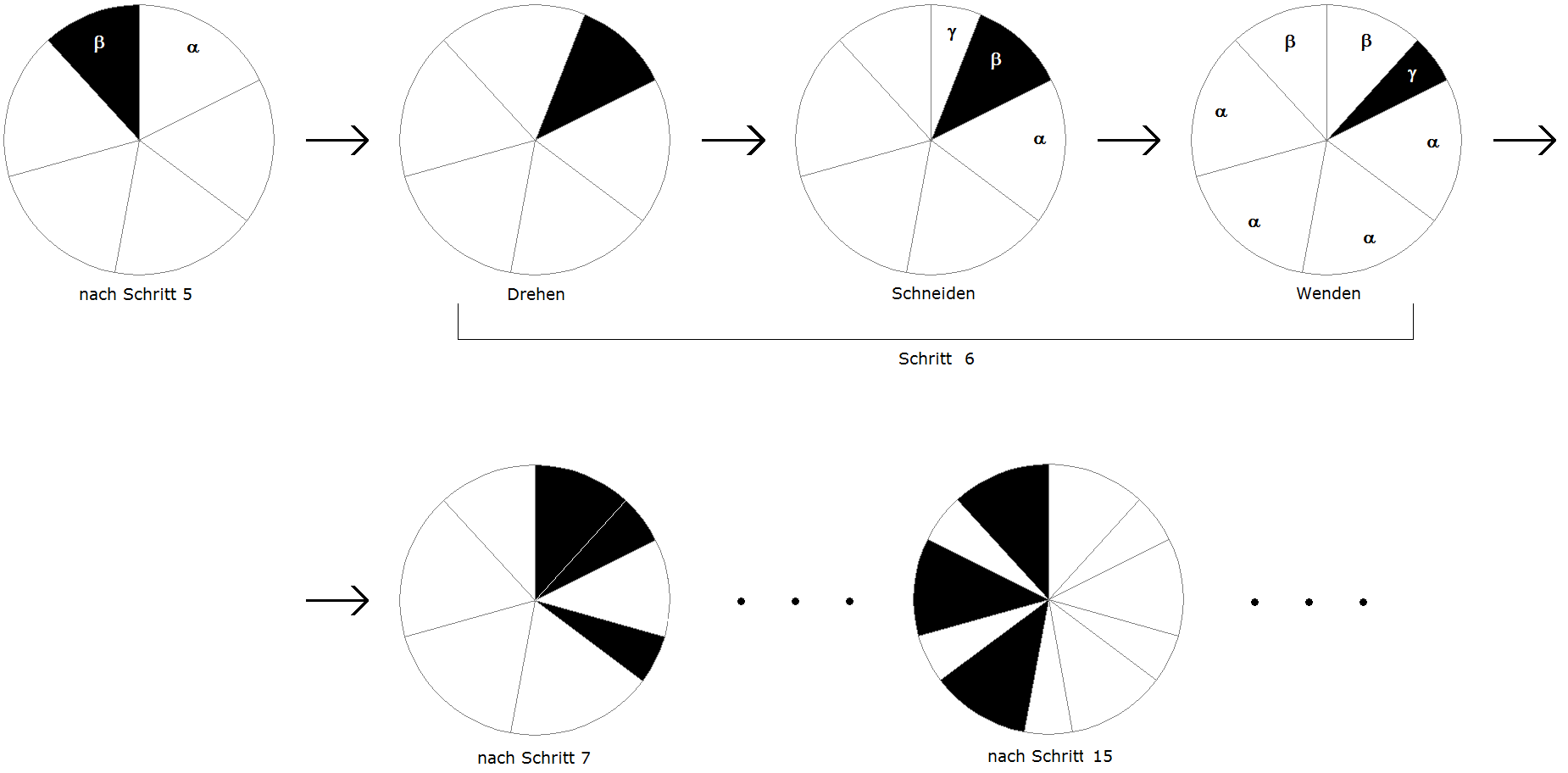
Bild 3 α = 360°·3/17 Was sieht man in Bild 3?
|
Was sind die üblichen Reaktionen, wenn die Lösung noch nicht verraten wurde ?
|


| Nach r Schritten, r ≥ 2n | Drehen um α | Wenden | Nach r+1 Schritten | |
| Winkel für Schnittlinien |
j·α , j = 0 ... n --------------------------- j·α - γ , j = 1 ... n |
j·α , j = 1 ... n γ → ---------------------- j·α - γ , j = 2 ... n 0° |
α - γ |
j·α , j = 0 ... n j·α - γ , j = 1 ... n |

|
Zusammenfassung: Lage der Schnittlinien
α = 360°·q, q ∈(0,1); α ist der Zentriwinkel der Tortenstücke. Der triviale Fall: q = 1/m, m ∈ N, m ≥ 2 → m Schnittlinien bei α·j/m, j = 0 ... m-1 (entspricht den Schritten 0 ... m-1 ) . Der nichttriviale Fall: q kein Stammbruch, n = ⌊1/q⌋, 360°/(n+1) < α < 360°/n → 2n+1 Schnittlinien bei Winkeln j·α, j = 0 ... n und j·α - γ, j = 1 ... n (entspricht den Schritten 0 ... 2n ). → n+1 β- Winkel, n γ-Winkel . Sobald alle diese Schnitte vorliegen, bleibt das Schnittmuster in allen weiteren Schritten identisch erhalten. |
|
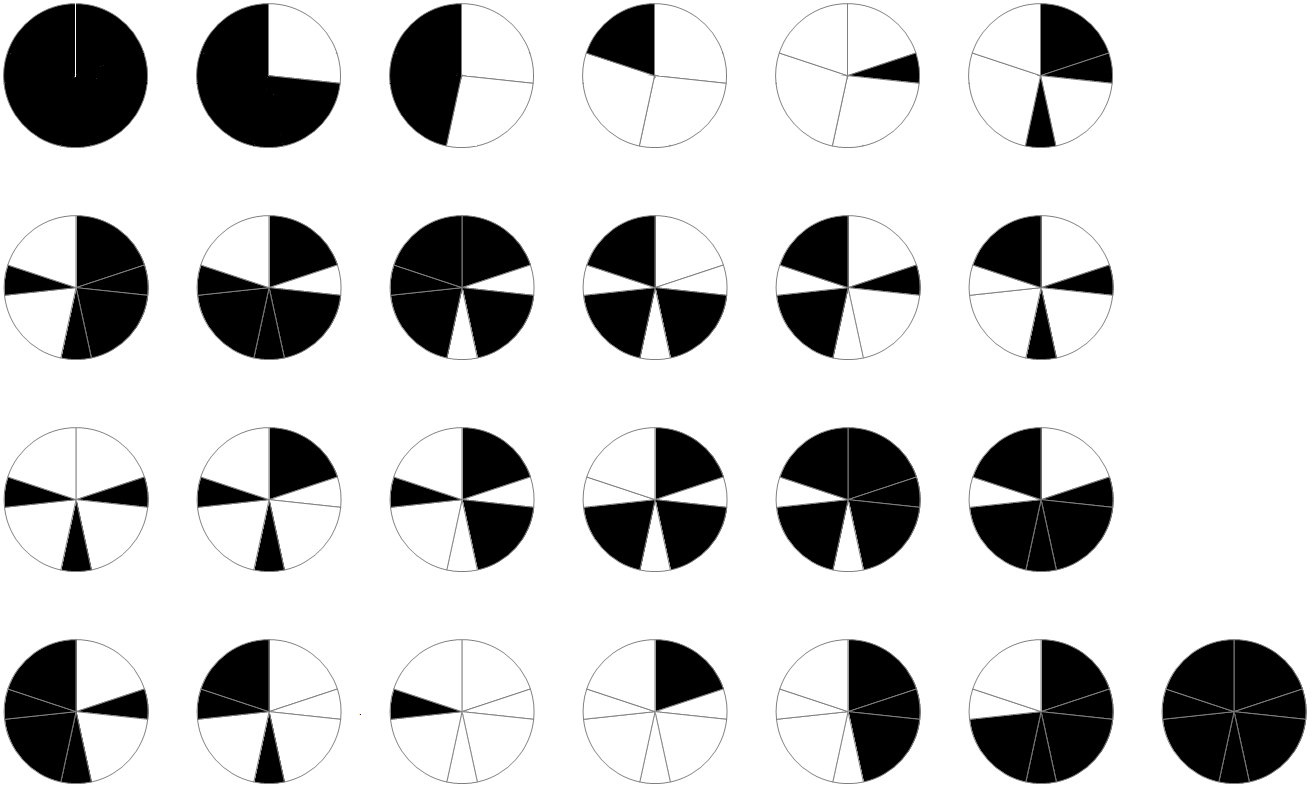
Zusammenfassung: Farbwechsel; Anzahl der Schritte bis zum Ziel
α Zentriwinkel der Tortenstücke. Der triviale Fall: α = 360°/m, m ∈ N, m ≥ 2 → s(m) = 2m Schritte. Der nichttriviale Fall: 360°/(n+1) < α < 360°/n → s(n) = 2n(n+1) Schritte. Die Folge s(n) findet man in der Datenbank OEIS unter A046092. Ganz hell wird die Torte nie. |
|
Zum Schluss nochmal alles Wesentliche
Erstaunlich, aber wahr: Jede beliebige Größe der Tortenstücke (mit Winkel α ) führt in endlich vielen Schritten zurück zum Ausgangszustand einer ganz dunklen Torte. Der Grund dafür – bei irrationalen Winkeln – liegt in der Verlagerung je einer Schnittlinie bei jedem Wenden eines Tortenstücks. Ganz einfach ist das natürlich für α = 360°/m : m Schnittlinien, 2m Schritte, Torte ganz hell nach m Schritten. Interessant ist nur der Fall 360°/(n+1) < α < 360°/n . Schon wenn man zweimal rundum geschnitten hat, ist ein konstantes Schnittmuster entstanden, so dass ab dann nicht mehr geschnitten, sondern nur noch gedreht und gewendet werden muss. Das Schnittmuster hat dann 2n+1 Schnittlinien. Das Ziel wird nach 2n(n+1) Schritten erreicht, ohne dass die Torte auf diesem Weg ganz hell wird. Die Anzahl der erforderlichen Schritte hängt also nicht davon ab, wie "kompliziert" α gewählt wird; insbesondere kann α ein irrationaler Bruchteil von 360° sein. Woher stammt dieses Problem? Das ist nicht bekannt; man weiß weder, wie alt es ist noch wer es ersonnen hat (mein Kenntnisstand – nach einiger Recherche – von 2022-03-29). Es ist Peter Winkler zu verdanken, dass er das Problem in seinem Buch Mathematical Mind-Benders vorgestellt hat. Er hat es aus einer französischen Quelle, weiß aber auch nichts Weiteres über seine Geschichte. |
Stand 2022-03-29
Inhalt Blog | voriger Eintrag | nächster Eintrag
Manfred Börgens | Zur Leitseite