Dodekaeder    MB Matheblog # 19 Inhalt Blog
voriger Eintrag    nächster Eintrag		 zur Leitseite
Index der gesamten Website

2022-05-30


Sonnenuhren Teil 2

Mobile äquatoriale analemmatische Sonnenuhr                    Kommentare sind willkommen.


In Bild 1 sehen wir eine alte äquatoriale Sonnenuhr in Peking. Man erkennt die typischen Eigenschaften solcher Uhren: Das Zifferblatt ist gegenüber der Senkrechten um einen Winkel geneigt, der der geographischen Breite entspricht; der Zeiger steht senkrecht zum Zifferblatt; der Zeigerschatten fällt im Sommerhalbjahr von oben und im Winterhalbjahr von unten auf das Zifferblatt (also wurde das Foto im Winterhalbjahr aufgenommen).

Pekinger Sonnenuhr

Bild 1   Äquatoriale Sonnenuhr in Peking    Quelle und Autor   Lizenz

Die Sonnenuhr in Bild 1 ist zwar weder mobil noch analemmatisch, soll aber als Ausgangspunkt unserer Überlegungen dienen. Es gibt viele verschiedene  –  auch sehr einfallsreiche  –  Ausfertigungen äquatorialer Sonnenuhren, aber hier beschränken wir uns auf das Grundmodell mit kreisförmigem Zifferblatt und einem Stab als Schattenwerfer; der Schatten des Stabs dient als (Uhr-)Zeiger.

Dieser Beitrag soll die mathematischen Grundlagen angeben, die zur Konstruktion einer äquatorialen Sonnenuhr mit einem möglichst genauen Analemma benötigt werden. Das bedeutet, dass jederzeit und überall  –  falls die Sonne scheint  –  die wahre Sonnenzeit um die Zeitgleichung korrigiert wird, um die mittlere Sonnenzeit zu erhalten. Sofern die Berechnungen nicht unmittelbar mit elementarer Trigonometrie durchgeführt werden können, folgen sie aus der Geo-astronomischen Formelsammlung auf dieser Website.

Es werden im Folgenden zahlreiche konkrete numerische Werte angegeben. Diese sind meist gerundet; sie können schon deshalb nicht genau sein, weil nicht zwischen Gemein- und Schaltjahren unterschieden wird. U.a. ist daher der Zusammenhang zwischen der Deklination und dem Datum ein wenig unscharf.

1. Eigenschaft: Äquatoriale Sonnenuhr
  • Der Stab ist zum Himmelsnordpol und -südpol ausgerichtet.

  • Das Zifferblatt steht senkrecht zum Stab. Dieser geht durch den Mittelpunkt des Zifferblatts.

  • Daraus folgt:

    • Das Zifferblatt steht parallel zum Äquator.

    • Der Winkel zwischen Zifferblatt und der Senkrechten ist gleich dem Absolutbetrag der geographischen Breite.

    • Die Einteilung in Stunden und Minuten am Rand des Zifferblatts ist äquidistant; eine Stunde entspricht einem Winkel von 15°, eine Minute entspricht einem Winkel von 15'.

    • Der Stab steht parallel zur Erdachse.

    • Der Winkel zwischen Stab und Untergrund ist gleich dem Absolutbetrag der geographischen Breite.

  • Es folgt weiterhin, dass der Stabschatten (Zeiger) im Sommerhalbjahr auf die Oberseite und im Winterhalbjahr auf die Unterseite des Zifferblatts fällt. Dies gilt sowohl für die Nord- wie die Südhalbkugel der Erde. Deshalb muss das Zifferblatt angemessen hoch angebracht werden, so wie in Bild 1 oder bei der Sonnenuhr in Blog # 18. In den Polregionen steht das Zifferblatt fast waagerecht, in Äquatornähe fast senkrecht.

Die Ablesung der Sonnenuhr führt dann auf die wahre lokale Sonnenzeit. Zum Vergleich mit der bürgerlichen Zeit (also mit der Armbanduhr) müssen noch folgende Anpassungen vorgenommen werden:
Beispiel: Wir stellen eine einfache äquatoriale Sonnenuhr (also ohne Analemmakorrektur) im Westen Deutschlands bei  6,5° Ost  am  20. September  auf. Die Zeitgleichung beträgt an diesem Datum  +7',  die Sonne geht also  7  Minuten gegenüber der mittleren Zeit vor. Die Sonnenuhr zeigt  9:30 Uhr  an:

  09:30 Uhr  wahre lokale Sonnenzeit
= 09:23 Uhr  mittlere lokale Sonnenzeit
= 09:57 Uhr MEZ  (denn  MEZ  bezieht sich auf  15° Ost; die Differenz von  8,5° entspricht  34')
= 10:57 Uhr  Sommerzeit, also aktuelle bürgerliche Zeit


2. Eigenschaft: Mobile Sonnenuhr
  • Will man eine äquatoriale Sonnenuhr an verschiedenen Orten verwenden, ohne die Konstruktion zu ändern, muss der Winkel zum Untergrund variabel einstellbar sein. Bei einer Konstruktion wie in Bild 1 müsste das Zifferblatt ein Scharnier am Fußpunkt erhalten. Einfacher scheint es zu sein, den Stab mit einem Scharnier am Untergrund zu befestigen, so wie in Blog # 18.

  • Weiter unten werden wir sehen, dass sich die Mobilität insbesondere auf die Verwendung eines Analemmas erstreckt. Bei anderen Sonnenuhren ändert sich die Schattenlänge, und damit auch das Analemma, mit dem Breitengrad des Beobachters  –  die Schattenlänge bei der äquatorialen Sonnenuhr ist dagegen unabhängig von der geographischen Breite.

  • So erhält man eine mobile äquatoriale Sonnenuhr, die universell einsetzbar ist: An allen Orten, zu allen Jahreszeiten, und solange die Sonne scheint.


Äquatoriale Sonnenuhren liefern quasi von selbst eine weitere schöne Funktion: Man kann die Deklination der Sonne und damit das Datum ablesen, wobei man dabei allerdings keine sehr hohe Präzision erwarten kann. Diese Funktion ist auch eine Grundlage für die Einbeziehung des Analemmas weiter unten. Die Schattenlänge hängt vom Einfallswinkel der Sonnenstrahlen und somit von der Deklination ab, und umgekehrt, siehe (1):

(1)

δ ∈ [-23,44°, 23,44°] : Deklination der Sonne

s : Stablänge

a = s·cot(|δ|) Schattenlänge

a ∈ [s·cot(23,44°), + ∞) ≈ [s·2,306, + ∞)

δ = ± arccot(a/s), "+" für die Nordsommerseite des Zifferblatts, "-" für die Nordwinterseite


In (1) ist  a  nur definiert für  δ ≠ 0 ,  also nicht zu den Äquinoktien. Denn zu Frühlings- und Herbstanfang laufen die Sonnenstrahlen parallel zur Ebene des Zifferblatts und lassen den Stabschatten unendlich lang werden.

Mit (1) kann man ein Zifferblatt herstellen, das die Deklination auf konzentrischen Kreisen um den Mittelpunkt anzeigt. Wir wollen im Folgenden annehmen, dass der Radius des Zifferblatts zu  1  normiert ist. Wegen  a ∈ [s·2,306, + ∞) muss der Stab eine Mindestlänge haben, wenn der Schatten immer den Rand des Zifferblatts erreichen soll:

(2)  s ≥ 1/2,306 ≈ 0,4336


Andererseits soll  a  in (0,1] liegen, damit man die Deklination ablesen kann. Für  δ = 0  geht das natürlich nicht. Nur wenn  s·2,306  deutlich kleiner als  1  ist, lässt sich nach (1) ein bestimmter Bereich der Deklinationen ablesen, siehe die folgende Tabelle mit Beispielen für konkrete Stablängen  s = s1 :

s1 amin |δ|min
0,02 0,0461 1,146°
0,05 0,1153 2,862°
0,1 0,2306 5,711°
0,2 0,4613 11,31°

Tabelle 1   amin ≈ s1·2,306    |δ|min = arccot(1/s1) = arctan s1

Beispiel: Für ein Zifferblatt mit Radius  1 m  und einem Stab der Länge  5 cm  entnimmt man der Tabelle 1, dass der Zeiger (also der Schatten) mindestens die Länge  11,53 cm  hat und nur Ablesungen der Deklination außerhalb des Bereichs (-2,862°, 2,862°) erlaubt. Die Einschränkung der Breite bedeutet, dass in der Zeit  14.-28. März  und  17.-30. September  die Deklination (→ Tabelle) nicht abgelesen werden kann.

Tabelle 1 zeigt, dass die Forderung in (1) mit der Ablesung der Deklinationen unverträglich ist. Aber das lässt sich lösen. Man montiert auf den Stab (Mindestlänge  0,4336  nach (2)) eine Kugel oder eine andere Markierung, die an der Höhe  s1  des Stabes sitzt;  s1  kann dann z.B. einen der Werte aus der Tabelle oder auch Zwischenwerte haben. Ist  s1  festgelegt, so ist klar, welche  δ-Werte nicht angezeigt werden können; diese liegen immer um die Äquinoktien herum.

Auf das Zifferblatt lassen sich dann konzentrische Kreise für ausgewählte Deklinationen zeichnen. Der Radius des Kreises für ein konkretes  δ  ist dann nach (1) gleich  s1·cot(|δ|),  siehe Bilder 2 und 3.

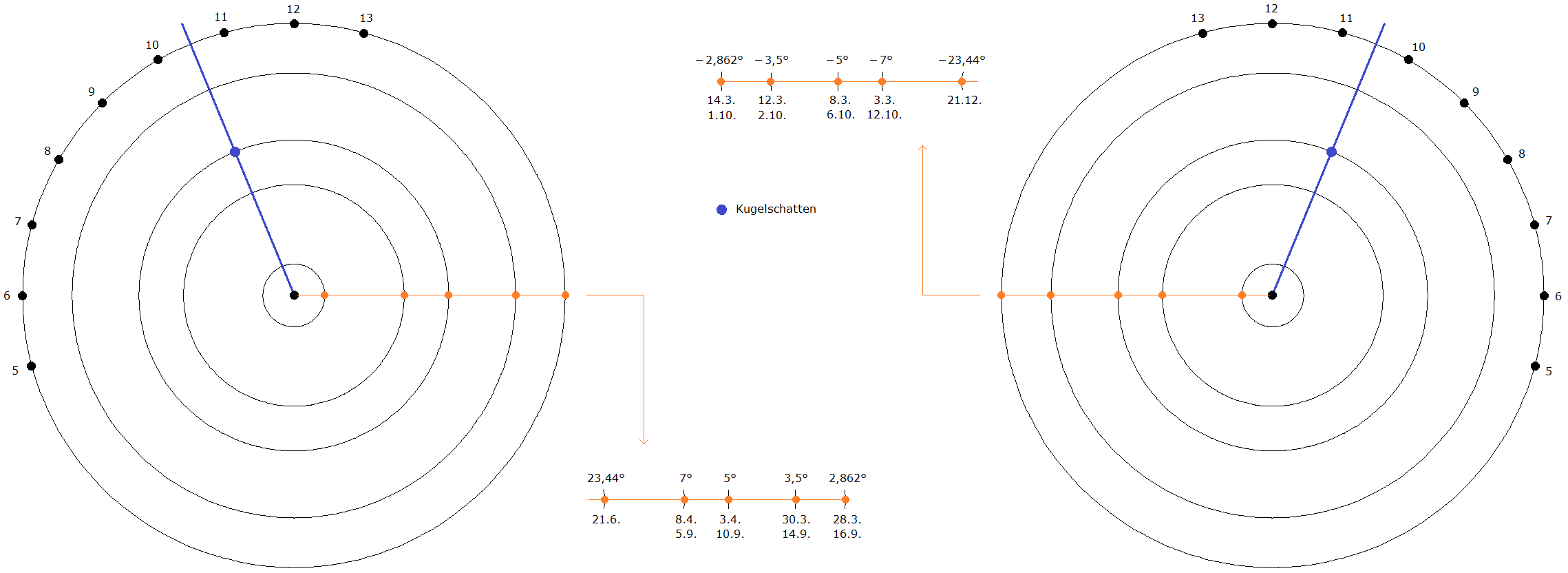
Sommer + Winter 0,05

Bild 2   Radius Zifferblatt  = 1   –   Stablänge bis Kugel  = 0,05   –   Die Sonnenuhr zeigt  10:30  an.

Links:    Deklination  5° ;  Datum  3. April  oder  10. September (→ Tabelle).
Links:      Um  10:30 Uhr  steht die Sonne auf den Breitengraden  φ ∈[-84,59°, 90°] über dem Horizont; siehe dazu (3) im nächsten grünen Kasten.
Links:      Nordhalbkugel  →  Sommer-Zifferblatt (Oberseite).
Links:      Südhalbkugel  →  Winter-Zifferblatt (Unterseite); nur für  φ ≥ -84,59°.

Rechts:  Deklination  -5° ;  Datum  8. März  oder  6. Oktober (→ Tabelle).
Links:      Um  10:30 Uhr  steht die Sonne auf den Breitengraden  φ ∈[-90°, 84,59°] über dem Horizont.
Links:      Nordhalbkugel  →  Winter-Zifferblatt (Unterseite); nur für  φ ≤ 84,59°.
Links:      Südhalbkugel  →  Sommer-Zifferblatt (Oberseite).


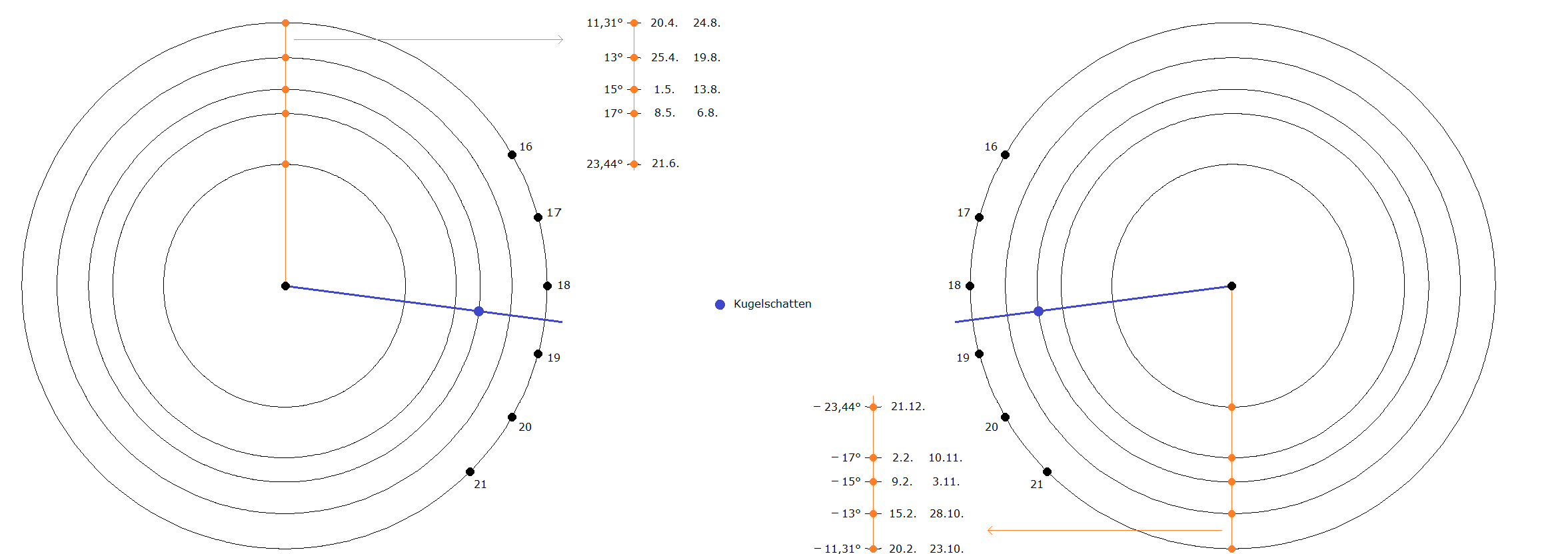
Sommer + Winter 0,2

Bild 3   Radius Zifferblatt  = 1   –   Stablänge bis Kugel  = 0,2   –   Die Sonnenuhr zeigt  18:30  an.

Links:    Deklination  15° ;  Datum  1. Mai  oder  13. August (→ Tabelle).
Links:      Um  18:30 Uhr  steht die Sonne auf den Breitengraden  φ ∈[25,97°, 90°] über dem Horizont; siehe dazu (3) im nächsten grünen Kasten.
Links:      Nordhalbkugel  →  Sommer-Zifferblatt (Oberseite); nur für  φ ≥ 25,97°.
Links:      Die Südhalbkugel liegt im Dunkeln, also auch das Winter-Zifferblatt (Unterseite).

Rechts:  Deklination  -15° ;  Datum  9. Februar  oder  3. November (→ Tabelle).
Links:      Um  18:30 Uhr  steht die Sonne auf den Breitengraden  φ ∈[-90°, -25,97°] über dem Horizont.
Links:      Die Nordhalbkugel liegt im Dunkeln, also auch das Winter-Zifferblatt (Unterseite).
Links:      Südhalbkugel  →  Sommer-Zifferblatt (Oberseite); nur für  φ ≤ -25,97°.


(3)

Unter den Bildern 2 und 3 wurden Angaben zu den geographischen Breiten gemacht, in denen die Sonne über dem Horizont steht. Dafür benötigt man jeweils denjenigen Breitengrad  φ ,  auf dem die Sonne zu einer vorgegebenen Uhrzeit  τ  auf- bzw. untergeht. Man findet dies in Formel (52) der Geo-astronomischen Formelsammlung:

φ = arctan(cot δ cos τ)


Anmerkung 1 zur Technik

Wie lassen sich die bisherigen Ausführungen praktisch umsetzen? Ablesungen der Deklination sind offenbar in den äußeren Bereichen des Zifferblatts einfacher als in Mittelpunktnähe. Z.B. liegen zwischen den beiden inneren orangenen Punkten in Bild 2 dicht gedrängt und auf sehr kleinen Kreisen alle Deklinationen  |δ|∈[7°, 23,44°].  Bei kleinen Werten für  s1  lassen sich also kleine Deklinationen gut und große Deklinationen schlecht ablesen. Bild 3 zeigt den Aufbau des Zifferblatts für eine viermal so hohe Kugelposition  s1  wie in Bild 2; hier kann man die großen Deklinationen gut ablesen  –  die kleinen (|δ| < 11,31°) können dagegen gar nicht angezeigt werden. Es ist durchaus denkbar, dass die Sonnenuhr mit zwei oder mehreren austauschbaren Zifferblättern ausgestattet wird, um zu verschiedenen Jahreszeiten möglichst gute Ablesungen der Deklination zu ermöglichen. Dann müsste die Kugel verschieblich am Stab angebracht werden.

Das Problem der Äquinoktien lässt sich aber damit nicht vollständig lösen. Selbst wenn die Kugelhöhe  s1  nur  2%  des Zifferblattradius beträgt, können nach Tabelle 1 Deklinationen  |δ|∈(-1,146°, 1,146°)  nicht abgelesen werden; dies entspricht den Daten  19.-23. März  und  21.-26. September, das sind immerhin  11  Tage (→ Tabelle).

Deshalb gilt generell, dass möglichst große Zifferblätter vorzuziehen sind, solange sie die Mobilität nicht zu sehr einschränken. Diese erlauben dann auch eine ausreichend große Dichte der konzentrischen Kreise für die Deklinationen mit den zugehörigen Daten.


Die Möglichkeit zur Ablesung der Deklination mag eher theoretisch und durchaus verzichtbar erscheinen  –  auf einer Sonnenuhr wird man eher eine Datumsanzeige erwarten. Das sind aber stark verwandte Aufgaben für den Sonnenuhrbauer, denn Deklination und Datum hängen eng zusammen. Eine tagesgenaue Übersicht liefert eine → Tabelle.

Möchte man also die konzentrischen Kreise wie in den Bildern 2 und 3 mit Daten statt mit Deklinationen beschriften, so rechnet man zuerst das Datum auf die zugehörige Deklination um, siehe (4):

(4)

t : Tages-Nummer im Jahr

δ ≈ 0,4095·sin(0,016906·(t - 80,086)) im Bogenmaß nach [1]
δ ≈ 0,4095·sin(0,016906·(t - 80,086))·180/π im Gradmaß

a = s1·cot(|δ|) Kreisradien, siehe (1).

Kleine Verschiebung im Vierjahresrhythmus wegen der Schaltjahre.


Wir fassen nun alles zusammen, was von (1) bis (4) dargestellt und in den Bildern 2 und 3 veranschaulicht wurde:

3. Eigenschaft: Sonnenuhr mit Deklinations- oder Datumsanzeige
  • Aus der Länge des Schattens auf dem Zifferblatt lassen sich die Deklination der Sonne und das Datum ermitteln.

  • Macht man den Stab lang genug, um ganzjährig mit dem Zeiger den Rand des Zifferblatts zu erreichen (siehe (2)), so kann er nicht zur Anzeige von Deklination/Datum dienen, er ist dann nämlich zu lang. Also montiert man z.B. eine Kugel auf den Stab, die recht nahe dem Fußpunkt liegt (siehe Tabelle 1).

  • Zu den Deklinationen bzw. Daten gehören konzentrische Kreise um den Fußpunkt des Stabs. Ihre Radien ermittelt man mit (4), siehe auch Bilder 2 und 3.

  • Da das Zifferblatt doppelseitig ist (Sommer-/Winterhalbjahr), lässt sich die Deklination eindeutig ablesen (positiv/negativ). Das Datum ist doppeldeutig, da zu jeder Deklination zwei Daten gehören.

  • Zu den Äquinoktien werden die Schatten des Stabes bis zur aufgesetzten Kugel unendlich lang. Deshalb gibt es bei jeder Positionierung der Kugel einige Tage vor und nach den Äquinoktien, an denen Deklination bzw. Datum nicht abgelesen werden können.

  • Falls die Konstruktion der Sonnenuhr austauschbare Zifferblätter für die konzentrischen Kreise erlaubt, kann man die Kugel auf dem Stab verschieblich machen und damit anpassbar auf die verschiedenen Beschriftungen der Zifferblätter. Beispielsweise könnte eine Beschriftung in der Nähe des Randes des Zifferblatts sehr nahe an die Äquinoktien heranreichen  –  dann sitzt die Kugel sehr nahe am Fußpunkt (siehe erste Zeile in Tabelle 1); eine andere Beschriftung, die eine bessere Ablesung um den Sommer- und Winteranfang herum ermöglicht, würde mit einer höheren Kugelposition erreicht (siehe letzte Zeile in Tabelle 1).


Nun zum Analemma, dem eigentlichen Kern dieses Beitrags. Ein Analemma ist eine geometrische Figur, die die Zeitgleichung, also die Abweichung der lokalen wahren Sonnenzeit (wie sie von einer Sonnenuhr angezeigt wird) von der lokalen mittleren Sonnenzeit (die der bürgerlichen Zeit entspricht  –  modulo der Längengradkorrektur und ggfs. der Sommerzeitkorrektur) in Abhängigkeit vom Datum darstellt. Man kennt  → Bilder des Analemmas am Himmel oder auf Sonnenuhren (aber nicht auf äquatorialen), die die Form einer Acht haben.

Will man ein Analemma für eine äquatoriale Sonnenuhr konstruieren, erhält man eine andere Figur: Die Acht wird zerschnitten und die beiden Teile werden auf Ober- und Unterseite aufgebracht  –  mit Ausnahme eines Streifens um die Äquinoktien.

Wir werden sehen, dass die äquatoriale Sonnenuhr die Verwendung des Analemmas besonders begünstigt. Dies liegt daran, dass im Gegensatz zu anderen Sonnenuhren die Schattenlänge nicht vom Breitengrad des Beobachters abhängt.  –  Allerdings gibt es auch einen Nachteil: Wie weiter oben schon erläutert, gibt es immer Intervalle um die Äquinoktien, in denen nur die Uhrzeit, nicht aber das Datum abgelesen werden kann, und somit auch nicht die Zeitgleichung.

Wie die Zeitgleichung vom Datum abhängt, wird in (5) beschrieben:

(5)

t : Tages-Nummer im Jahr

z ≈ 60·(-0,171·sin(0,0337·t + 0,465) - 0,1299·sin(0,01787·t - 0,168))
Zeitgleichung in Minuten nach [1]

z positiv: Sonnenuhr geht vor (gegenüber der mittleren Sonnenzeit)
z negativ: Sonnenuhr geht nach


Das Analemma für die äquatoriale Sonnenuhr wird als Parameterkurve auf das Zifferblatt aufgebracht. Damit es zu jeder Uhrzeit verwendet werden kann, muss es um den Mittelpunkt des Zifferblatts rotieren können. Der Parameter für die Kurve ist das Datum  t .  Abhängig von  t  ist der Abstand  a  des Kugelschattens vom Mittelpunkt und der Winkel  γ  auf dem Zifferblatt, der sich aus der Zeitgleichung errechnen lässt. (a,γ) sind also Polarkoordinaten, siehe (6).


(6)

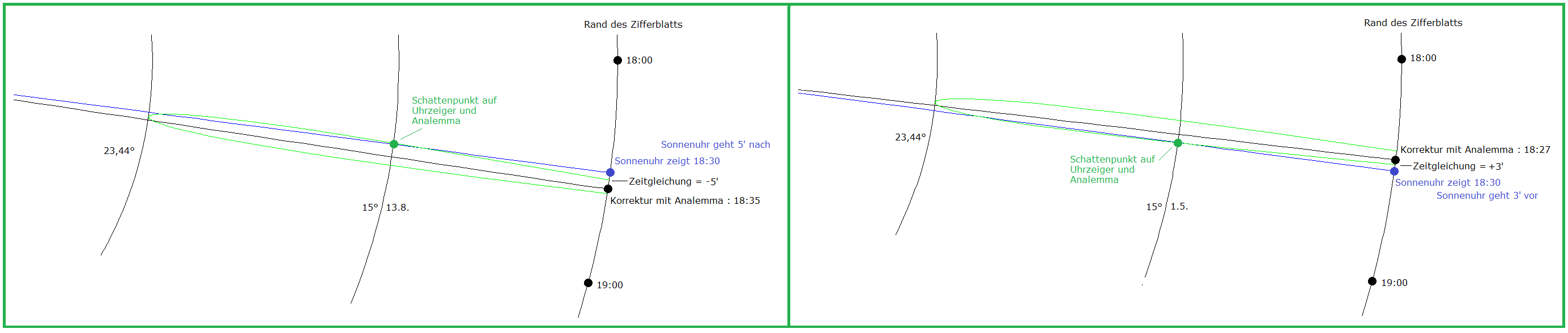
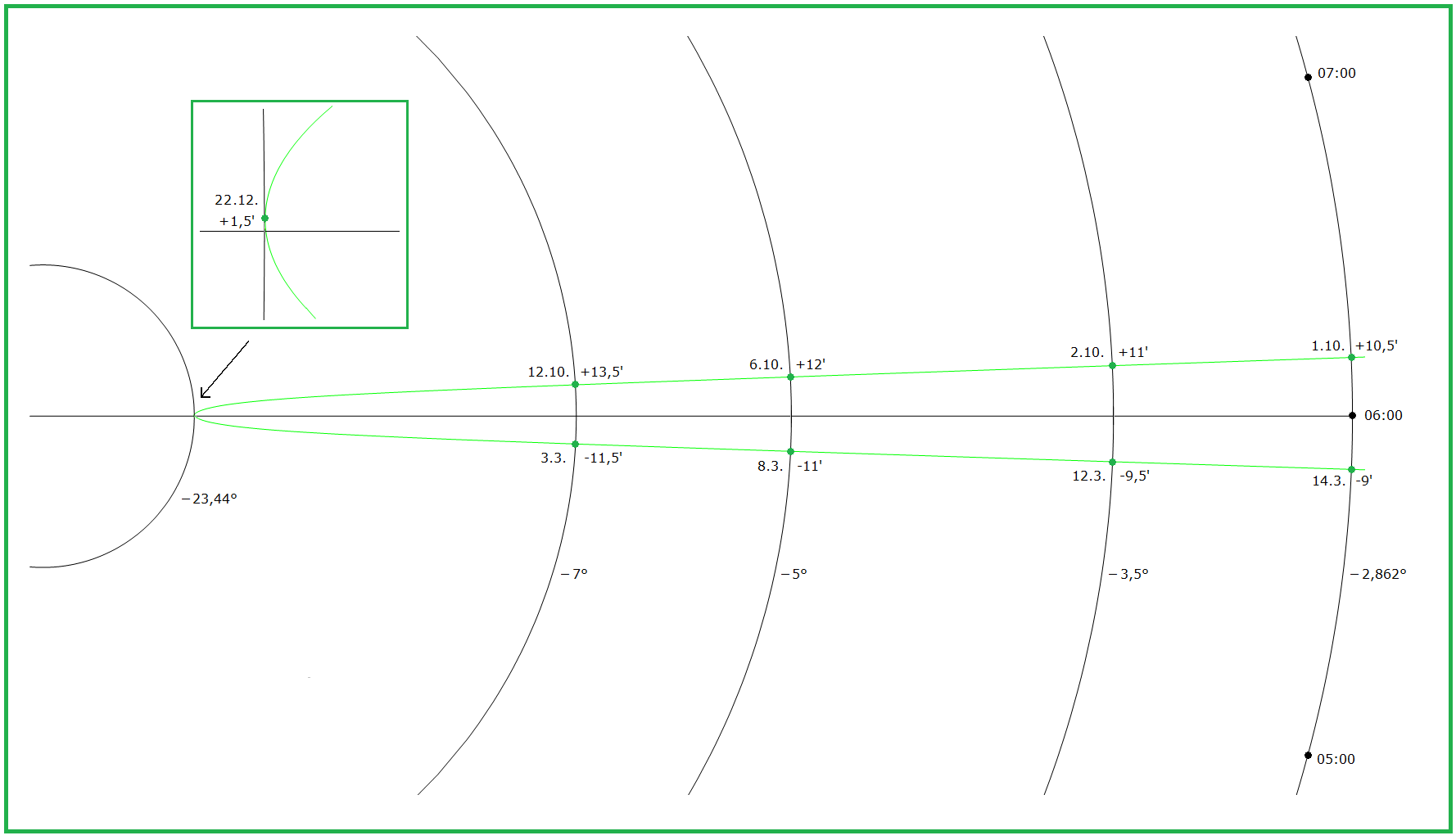
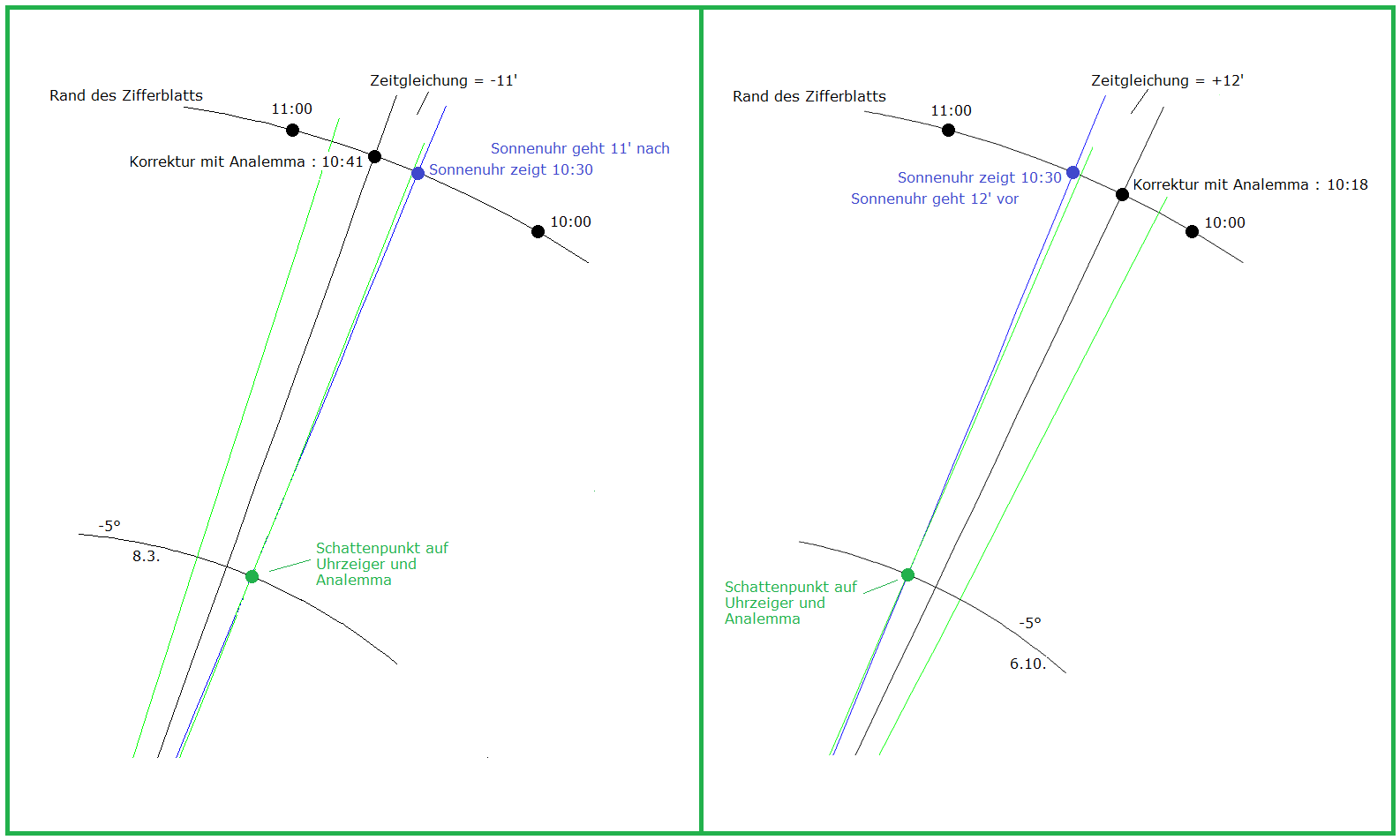
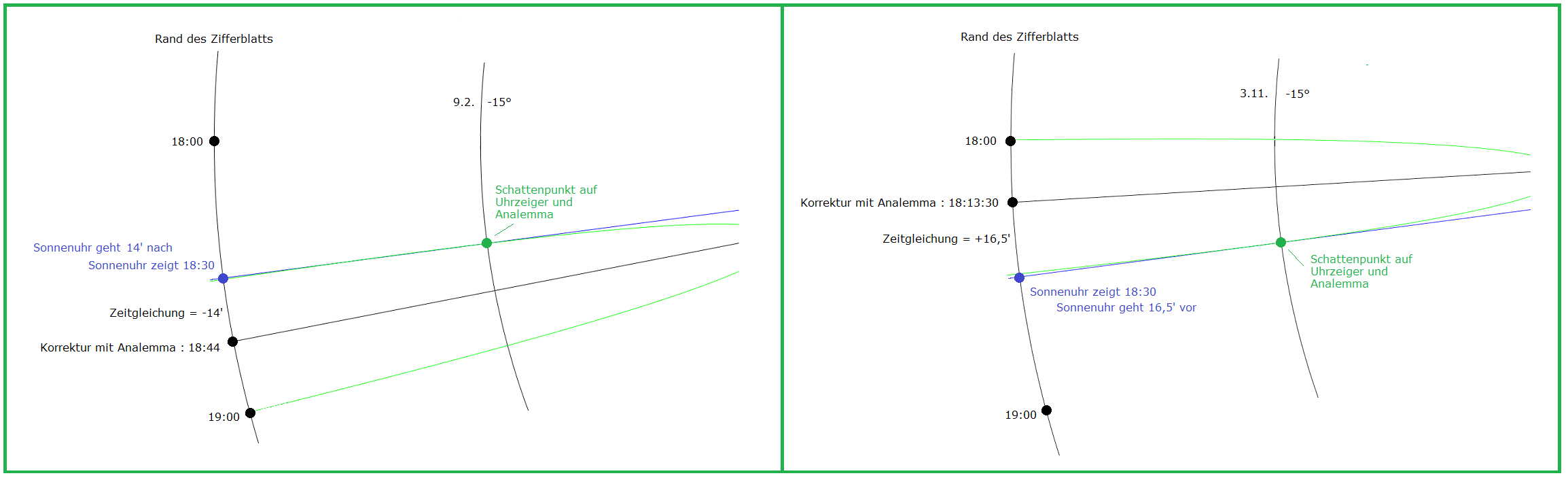
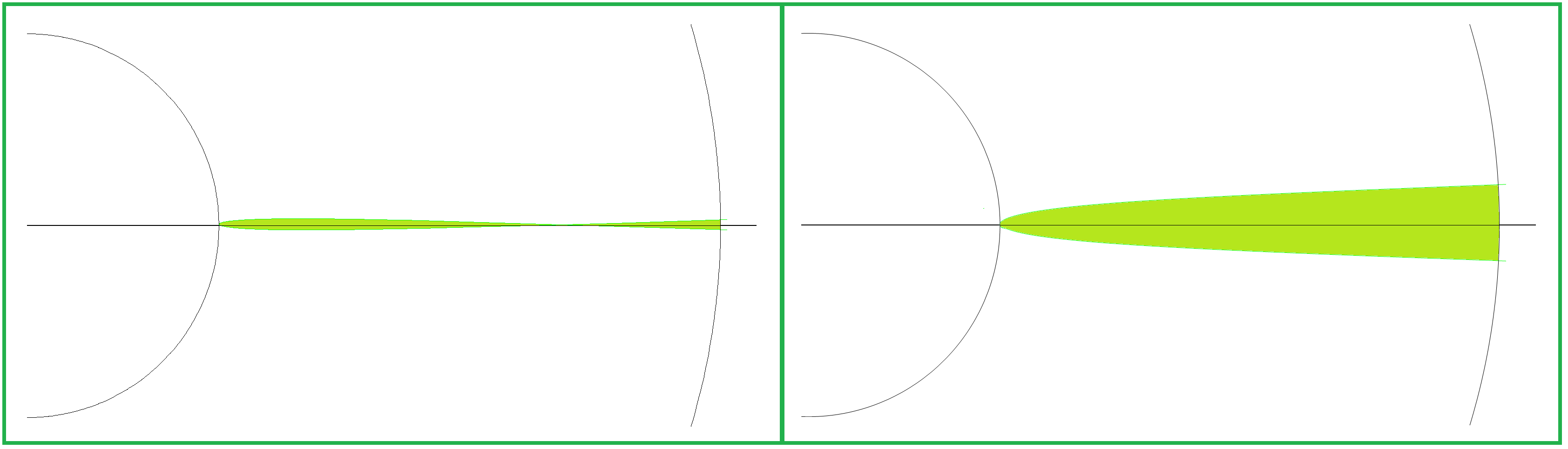
(6a)  Analemma für mittlere Sonnenzeit 12 Uhr

Polarkoordinaten:

   Radius = a   Funktion von t nach (4)

   Winkel = γ   Abweichung gemäß Zeitgleichung z, also Funktion von t nach (5)

Oberseite der Sonnenuhr:  γ = 90° - z/4  im Gradmaß
Unterseite:               γ = 90° + z/4

Begründung: Die im Folgenden verwendeten Koordinaten (a·cos γ, a·sin γ) beschreiben einen Kreis mit Radius a, im Gegenuhrzeigersinn durch den Punkt (a,0) für γ = 0 und durch (0,a) für γ = 90° (dies entspricht 12 Uhr).  —  z ist in Zeitminuten gemessen; eine Zeitminute entspricht auf dem Zifferblatt dem Winkel 0,25°, also beträgt die Abweichung durch die Zeitgleichung z/4. Geht die Sonnenuhr vor (nach), so ist z positiv (negativ) und die mittlere Sonnenzeit (hier 12 Uhr) demnach früher (später) als die wahre Sonnenzeit. Auf der Oberseite der Sonnenuhr läuft der Zeiger im Uhrzeigersinn, auf der Unterseite im Gegenuhrzeigersinn, damit erklären sich die Vorzeichen in den Formeln für γ.

Parameterkurve für das Analemma in kartesischen Koordinaten (x,y):

(x,y) = (a·cos γ, a·sin γ)  Parameter ist t; a und γ sind Funktionen von t


(6b)  Analemma für mittlere Sonnenzeit h Uhr

Jede volle Stunde entspricht auf dem Zifferblatt einem Winkel von 15°. Also liegen (h-12)·15° zwischen 12 Uhr und h Uhr. Damit erhalten wir die Parameterkurve:

(x,y) = (a·cos(γ ± (h-12)·15°), a·sin(γ ± (h-12)·15°))  "-" für Oberseite, "+" für Unterseite

Im folgenden Bild 4 wurde das Analemma auf der Oberseite waagerecht gelegt, für die mittlere Sonnenzeit 18 Uhr. Im Bild 7 weiter unten wurde das Analemma auf der Unterseite waagerecht gelegt, für die mittlere Sonnenzeit 6 Uhr. Die in den beiden Bildern dargestellte Parameterkurve wurde also gezeichnet mit

(x,y) = (a·cos(γ - 90°), a·sin(γ - 90°))


Nun folgen mehrere Bilder, die beispielhaft die Sonnenuhr mit Analemma zeigen. Die Bilder 4 bis 6 zeigen die Oberseite der Uhr für den Nordsommer und die Unterseite für den Südwinter.

Zunächst wird in Bild 4 das Zifferblatt mit Analemma, aber ohne Uhrzeiger für die wahre Sonnenzeit (blau in den Bildern 2 und 3) gezeigt. In dieser Position liegt das Analemma für die mittlere Sonnenzeit  18 Uhr .  Der waagerechte schwarze Strich liegt immer in dieser relativen Position zum Analemma (grün)  –  unabhängig davon, wie das Analemma gedreht wird  —  er wandert also mit. Er dient in allen weiteren Bildern als zweiter Uhrzeiger und zeigt die mittlere Sonnenzeit an.

Bild 4 zeigt konzentrische Kreise für ausgewählte Deklinationen und die entsprechenden Daten. Außerdem sind die zugehörigen Werte der Zeitgleichung in Minuten entlang des Analemmas eingetragen.

Die Darstellung des Analemmas wird hier auf eine einzige Position der Kugel auf dem Stab beschränkt, nämlich für  s1 = 0,05 .  Andere Positionen würden das Analemma stauchen oder strecken, siehe dazu Bild 6.

Die Datumsangaben in Bild 4 (und natürlich noch weitere, möglichst dicht) werden auf dem Analemma eingetragen.

Zu Bild 4 gehört die zweite Zeile in Tabelle 1 und die linke Skizze in Bild 2.

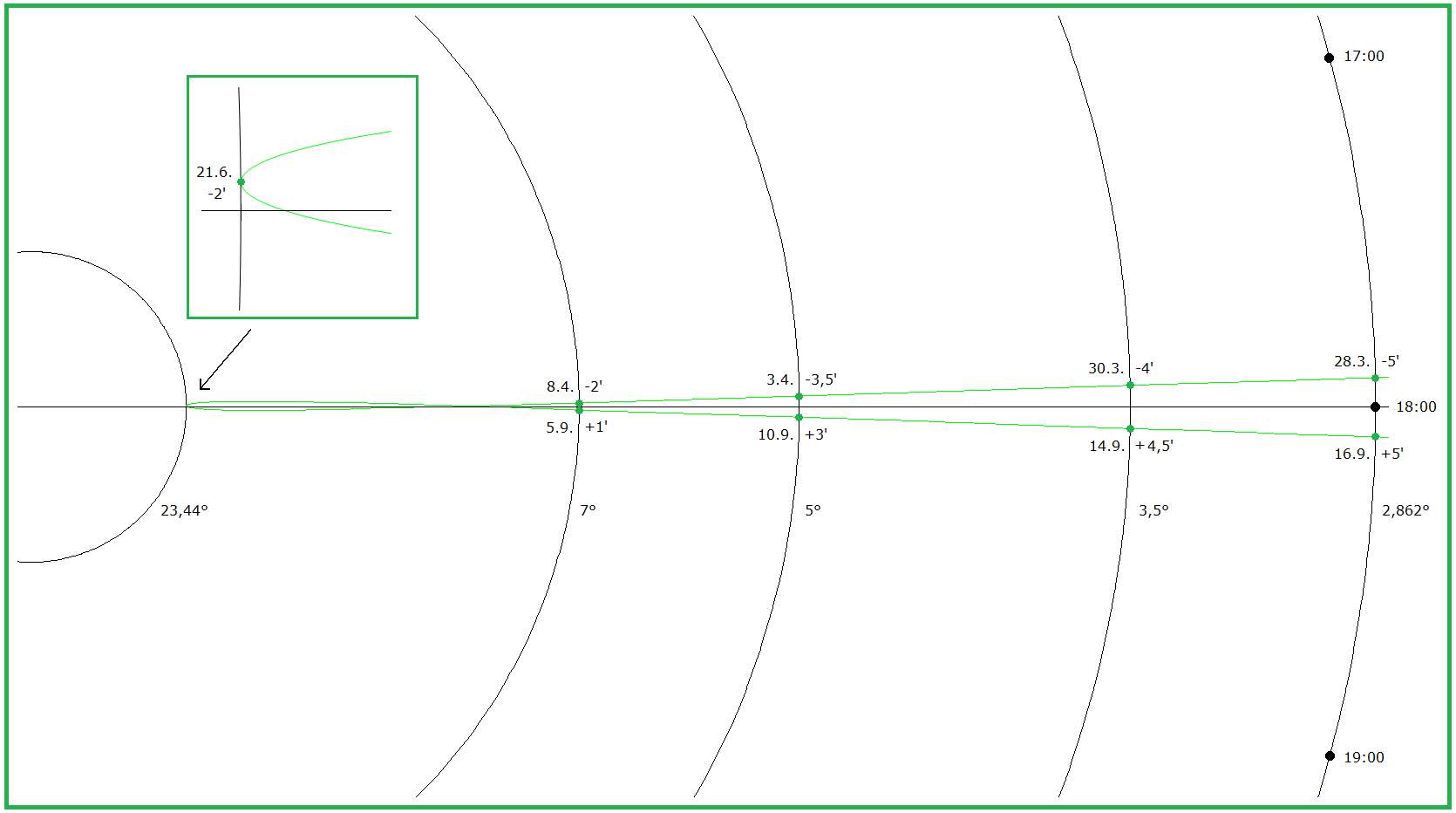
Analemma Nordsommer waagerecht .05

Bild 4   Analemma (grün) für  s1 = 0,05 ,  mit zugehörigem schwarzen Zeiger für  18 Uhr  mittlere Sonnenzeit im Nordsommer


Das folgende Bild 5 steht in direktem Zusammenhang mit der linken Skizze in Bild 2. Von dort wurde nur der  5°-Kreis übernommen und der blaue Schattenpunkt wurde grün, um seine Lage auf dem Analemma zu verdeutlichen. Für diese Deklination kommen zwei Daten in Frage:  3. April  (linke Skizze, Zeitgleichung  -3,5') und  10. September  (rechte Skizze, Zeitgleichung  +3').

Bild 5 zeigt, wie das Analemma angewendet wird. Man dreht es in eine Position, so dass es genau über den Schattenpunkt verläuft; die beiden Daten sind auf dem Analemma vermerkt (dafür muss man natürlich wissen, ob gerade Frühling oder Spätsommer ist). Dann zeigt der schwarze Zeiger am Analemma die mittlere Sonnenzeit an.

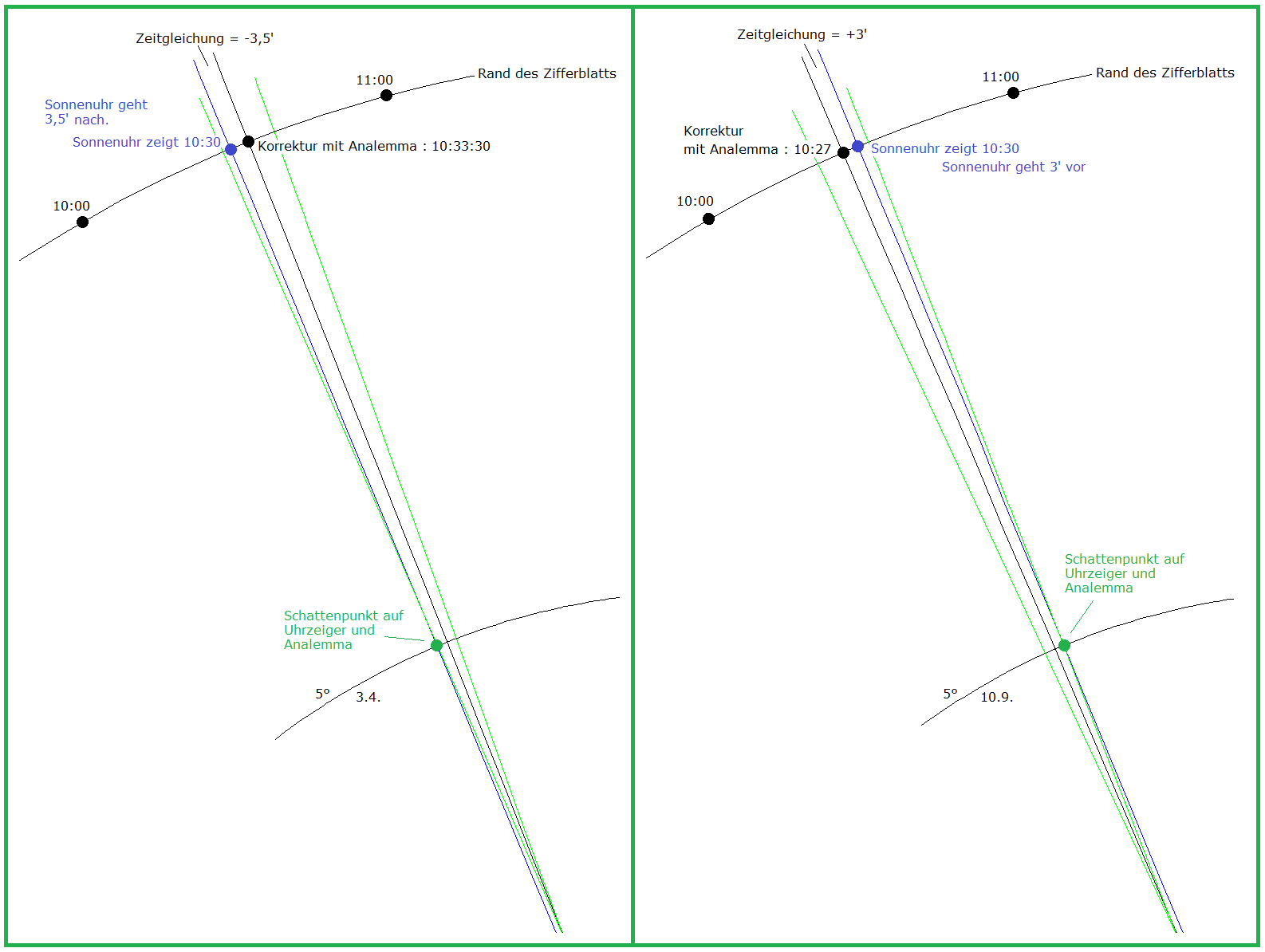
10:30 Zgl. Nordsommer .05

Bild 5   Analemma (grün) für  s1 = 0,05  und  δ = 5°, mit zugehörigem schwarzen Zeiger für die mittlere Sonnenzeit; blauer Zeiger für die wahre Sonnenzeit  10:30 Uhr .


Das folgende Bild 6 steht in direktem Zusammenhang mit der linken Skizze in Bild 3. Gegenüber Bild 5 ist hier die Kugel auf dem Stab nach oben auf die Position  0,2  geschoben worden. Es wurde nur der  15°-Kreis übernommen und der blaue Schattenpunkt wurde grün, um seine Lage auf dem Analemma zu verdeutlichen. Für diese Deklination kommen zwei Daten in Frage:  1. Mai  (rechte Skizze, Zeitgleichung  +3') und  13. August  (linke Skizze, Zeitgleichung  -5').

18:30 Zgl. Nordsommer .2

Bild 6   Analemma (grün) für  s1 = 0,2  und  δ = 15°, mit zugehörigem schwarzen Zeiger für die mittlere Sonnenzeit; blauer Zeiger für die wahre Sonnenzeit  18:30 Uhr .


In den Bildern 4 bis 6 wurde die Seite der Sonnenuhr behandelt, die vom Nordpol aus zu sehen ist. Nun zur Seite, die vom Südpol aus zu sehen ist. Die Bilder 7 bis 9 zeigen die Unterseite der Uhr für den Nordwinter und die Oberseite für den Südsommer.

Zunächst wird in Bild 7 das Zifferblatt mit Analemma, aber ohne Uhrzeiger für die wahre Sonnenzeit (blau in den Bildern 2 und 3) gezeigt. In dieser Position liegt das Analemma für die mittlere Sonnenzeit  6 Uhr.

Zu Bild 7 gehört die zweite Zeile in Tabelle 1 und die rechte Skizze in Bild 2.

Analemma Nordwinter waagerecht .05

Bild 7   Analemma (grün) für  s1 = 0,05 ,  mit zugehörigem schwarzen Zeiger für  6 Uhr  mittlere Sonnenzeit im Nordwinter


Das folgende Bild 8 steht in direktem Zusammenhang mit der rechten Skizze in Bild 2. Von dort wurde nur der  -5°-Kreis übernommen und der blaue Schattenpunkt wurde grün, um seine Lage auf dem Analemma zu verdeutlichen. Für diese Deklination kommen zwei Daten in Frage:  8. März  (linke Skizze, Zeitgleichung  -11') und  6. Oktober  (rechte Skizze, Zeitgleichung  +12').

10:30 Zgl. Nordwinter .05

Bild 8   Analemma (grün) für  s1 = 0,05  und  δ = -5°, mit zugehörigem schwarzen Zeiger für die mittlere Sonnenzeit; blauer Zeiger für die wahre Sonnenzeit  10:30 Uhr .


Das folgende Bild 9 steht in direktem Zusammenhang mit der rechten Skizze in Bild 3. Gegenüber Bild 8 ist hier die Kugel auf dem Stab nach oben auf die Position  0,2  geschoben worden. Es wurde nur der  -15°-Kreis übernommen und der blaue Schattenpunkt wurde grün, um seine Lage auf dem Analemma zu verdeutlichen. Für diese Deklination kommen zwei Daten in Frage:  9. Februar  (linke Skizze, Zeitgleichung  -14') und  3. November  (rechte Skizze, Zeitgleichung  +16,5').

18:30 Zgl. neg. Nordwinter .2

Bild 9   Analemma (grün) für  s1 = 0,2  und  δ = -15°, mit zugehörigem schwarzen Zeiger für die mittlere Sonnenzeit; blauer Zeiger für die wahre Sonnenzeit  18:30 Uhr .


Wir fassen nun alles zusammen, was von (5) und (6) dargestellt und in den Bildern 4 bis 9 veranschaulicht wurde:

4. Eigenschaft: Analemmatische Sonnenuhr
  • Die Zeitgleichung erfordert eine Korrektur der Sonnenuhr-Zeitanzeige, da die bürgerliche Zeit nur gleich lange Tage kennt, die wahre Sonnenzeit aber Schwankungen in der Tageslänge aufdeckt; die Zeitgleichung berechnet man mit (5) oder mit Tabellen oder Diagrammen, die man zahlreich im Internet findet.

  • Für eine äquatoriale Sonnenuhr gibt es zu jeder Position der Kugel auf dem Stab (für die Anzeige von Deklination und/oder Datum) je eine analemmatische Kurve auf der Ober- und Unterseite des Zifferblatts, die rotierbar sein muss; sie bildet die Zeitgleichung auf dem Zifferblatt ab und wird mit (6) berechnet.

  • Das Analemma sollte eine Datumsbeschriftung entlang der Kurve haben, da jeder konzentrische Kreis auf dem Zifferblatt zu zwei Daten gehört (siehe Bilder 2 bis 9).

  • Für das Analemma gilt die gleiche Einschränkung wie für die Ablesung von Deklination und Datum: Der Schatten an den Äquinoktien wird unendlich lang, so dass bei jeder Kugelposition ein gewisses Datumsintervall für die Ablesung ausfällt.

  • Die Ablesung der Zeitgleichung am Analemma gelingt  –  vor allem im Nordsommer  –  am besten in den äußeren Bereichen des Zifferblatts. Daher ist ein austauschbares Zifferblatt in mindestens zwei Ausführungen für verschiedene Kugelpositionen zu empfehlen.



Anmerkung 2 zur Technik

Ist eine äquatoriale Sonnenuhr mit Analemma mit einfachen Mitteln praktisch herstellbar? Über die austauschbaren Zifferblätter und die bewegliche Kugel am Stab wurde schon oben in Anmerkung 1 gesprochen. Das dürfte kein großes Problem darstellen. Die Herstellung des Analemmas erfordert für jede Kugelposition zwei rotierbare Zeiger (je einer für Ober- und Unterseite; schwarz in den Bildern 4 bis 9), an denen die analemmatischen Kurven befestigt sind. Da der Schattenpunkt immer auf der Kurve liegt, kann man das Analemma "füllen", also eine Fläche herstellen, was die Konstruktion vereinfachen dürfte, siehe Bild 10.

2 Analemmas für s1=.12

Bild 10   Analemma (grün) für  s1 = 0,12  mit zugehörigem schwarzen Zeiger für die mittlere Sonnenzeit. Links Nordsommer, rechts Nordwinter.

Wie man in Bild 10 sieht, ist der Spannweitenunterschied am äußeren Rand der beiden Zifferblätter beträchtlich. Bei sehr kleinen  s1  passen die beiden analemmatischen Kurven dort (fast) zusammen und bilden aneinandergefügt (fast) die liegende Acht, die man von anderen Sonnenuhren kennt. Aber bei sehr kleinen  s1  ist das Analemma noch viel dünner als in Bild 10 links (siehe Bild 4) und für große Deklinationen schwer ablesbar; auch die Aufbringung der Daten auf das Analemma ist dann schwierig. Hier ist  s1 = 0,12 ,  das ist ein eher großer Wert und bedeutet  δ = ± arctan 0,12 = ± 6,84°  auf dem Rand des Zifferblatts (siehe Erläuterung bei Tabelle 1). Der erwähnte Spannweitenunterschied ist also gut erklärbar; hier fehlen die Datumsintervalle  4. März  bis  7. April  und  6. September  bis  10. Oktober.  In den Bildern 2 bis 9 wurden  s1 = 0,05  und  s1 = 0,2  verwendet; die Zifferblätter mit Analemma in Bild 10 wären dazu eine gute Ergänzung.

Durch den Zeiger des Analemmas wird es möglich, das Zifferblatt mit der bürgerlichen Zeit statt der Sonnenzeit zu beschriften. Dazu muss man die Längengradkorrektur vornehmen, wie weiter oben unter dem Kasten für die 1. Eigenschaft erläutert wurde. Davon ist jedoch wegen der Umstellung auf Sommer- bzw. Winterzeit abzuraten. Außerdem verliert die Sonnenuhr dadurch ihre Mobilität  –  vielleicht will man sie ja mit in den Urlaub nehmen. Die Differenz zwischen der mittleren Sonnenzeit und der bürgerlichen Zeit muss man sich halt merken oder aufschreiben. Einen genialen Ausweg gäbe es natürlich: Der Rand des Zifferblatts mit den Uhrzeiten könnte als drehbarer Kreisring gefertigt werden.



Quelle

[1]  www.astronomie.info/zeitgleichung/



Kategorie: Geomathematik                    Kommentare sind willkommen.


Stand 2021-11-29

Inhalt Blog   |    voriger Eintrag   |    nächster Eintrag


Manfred Börgens   |   Zur Leitseite