Gleichmäßige Gitter Kommentare sind willkommen.
Einleitung
Gleichmäßige 2D-Gitter sind Rechtecke, die aus einer regelmäßigen Kachelung aus \(~n~\) kongruenten Rechtecken wie in Bild 1 aufgebaut sind. Die \(~n~\) Rechtecke müssen alle dieselbe Ausrichtung haben. Das linke Gitter in Bild 1 ist ein kartesisches 2D-Gitter oder aa-Gitter mit quadratischen Kacheln. Im rechten Gitter haben die Rechtecke verschiedene Seitenlängen; diese Gitter werden wir ab-Gitter nennen.
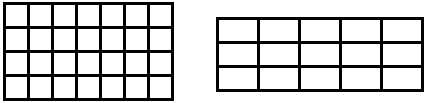
Bild 1 Gleichmäßige 2D-Gitter; links aa-Gitter (kartesisch), rechts ab-Gitter
Es gibt noch eine andere (äquivalente) Definition der gleichmäßigen 2D-Gitter. Kartesische Gitter können als Rechtecke mit ganzzahligen Seitenlängen und Flächeninhalt \(~n~\) beschrieben werden. Nicht-kartesische Gitter können als Rechtecke mit Seitenlängen \(~(m_1,~m_2 \cdot b)~\) und irrationalem \(~b~\) oder mit Seitenlängen \(~(m_1 \cdot a,~m_2 \cdot b)~\) und inkommensurablen \(~a,~b~\) beschrieben werden. In beiden Fällen ist \(~m_1 \cdot m_2=n~\) mit ganzzahligen \(~m_1,~m_2~\). – Mit dieser Definition kann man die Kachelränder innerhalb des äußeren Rechtecks weglassen.
In Bild 2 sehen wir gleichmäßige 3D-Gitter. Das sind Quader mit einer regelmäßigen Raumfüllung aus \(~n~\) kongruenten Quadern, die alle dieselbe Ausrichtung haben. Das linke Gitter in Bild 2 ist aus Würfeln aufgebaut und heißt kartesisches 3D-Gitter oder aaa-Gitter. Das Gitter in der Mitte ist ein aab-Gitter aus Quadern mit zwei verschiedenen Seitenlängen. Das rechte Gitter nennen wir abc-Gitter; es enthält Quader mit drei verschiedenen Seitenlängen.

Bild 2 Gleichmäßige 3D-Gitter; von links nach rechts: aaa-Gitter (kartesisch), aab-Gitter, abc-Gitter
Man kann eine äquivalente Definition für gleichmäßige 3D-Gitter angeben, die dem 2D-Fall entspricht. Kartesische Gitter können als Quader mit ganzzahligen Seitenlängen und Volumen \(~n~\) beschrieben werden. aab-Gitter sind Quader mit Seitenlängen \(~(m_1,~m_2,~m_3 \cdot b)~\) und irrationalem \(~b~\) oder mit Seitenlängen \(~(m_1 \cdot a,~m_2 \cdot a,~m_3 \cdot b)~\) und inkommensurablen \(~a,~b~\). abc-Gitter sind Quader mit Seitenlängen \(~(m_1,~m_2 \cdot b,~m_3 \cdot c)~\) und irrationalen, inkommensurablen \(~b,~c~\) oder mit Seitenlängen \(~(m_1 \cdot a,~m_2 \cdot b,~m_3 \cdot c)~\) und inkommensurablen \(~a,~b,~c~\). In allen diesen Fällen ist \(~m_1 \cdot m_2 \cdot m_3=n~\) mit ganzzahligen \(~m_1,~m_2,~m_3~\). – Mit dieser Definition kann man die Ränder der \(~n~\) Quader weglassen, die innerhalb des äußeren Quaders liegen.
Die folgenden Abschnitte behandeln die Anzahl der Möglichkeiten, \(~n~\) identische Rechtecke oder Quader zu gleichmäßigen Gittern zusammenzusetzen, modulo Rotation.
Teiler
Es soll eine Formel für die Anzahl der Teiler einer natürlichen Zahl \(~n~\) angegeben werden. Diese Anzahl ist ein wesentlicher Bestandteil der Lösung der Aufgabe am Ende der Einleitung. Wir schreiben \(~n~\) als eindeutiges Produkt seiner Primfaktoren \(~p_i~\):
\[\textbf{(1)}~~~n=\prod_i p_i^{h_i}\]
Die Teiler von \(~n~\) können jeden dieser Primfaktoren \(~p_i~\) mit Potenz \(~0~...~h_i~\) enthalten. Also gibt es \(~1+h_i~\) Möglichkeiten für das Auftreten von \(~p_i~\) (in einer beliebigen Potenz \(\ge~0\)) in einem Teiler von \(~n~\). Die Anzahl der Teiler von \(~n~\) (incl. \(~1~\) und \(~n~\)) wird mit \(~\tau(n)~\) bezeichnet:
\[\textbf{(2)}~~~\tau(n)=\prod_i ~(1+h_i)\]
Bemerkung: \(~n=\prod_i~ p_i^{h_i}~\) kann auch als unendliches Produkt gelesen werden, das alle Primzahlen \(~p_i~\) enthält, wenn man \(~h_i=0~\) zulässt. Dies ergibt eine Bijektion zwischen der Menge \(~\textbf{N}~\) der natürlichen Zahlen und dem Folgenraum \(~\textbf{N}_{\text{o}}^{\infty}~\) aller "finiten" Folgen von nicht-negativen ganzen Zahlen durch die Abbildung \(~n \longleftrightarrow (h_i)_{i \in \textbf{N}}~\), wobei "finit" die Bedeutung "enthält nur endlich viele von \(0~\) verschiedene Folgenglieder" hat. Also ist \(~\textbf{N}_{\text{o}}^{\infty}~\) abzählbar.
Mathematica:
\(~p_i~\) und \(~h_i~\) erhält man mit FactorInteger[n]
\(~\tau(n)~\) erhält man mit Length[Divisors[n]]
oder f=FactorInteger[n]; le=Length[f]; Product[1+f[[m]][[2]],{m,le}]
OEIS:
\(\tau(n)~=~\)\(\text{A000005}(n)\)
2D-Gitter (aa- und ab-Gitter)
Das kartesische Gitter im nächsten Bild enthält \(~n=28~\) Quadrate und ist ein \(~(4 \times 7)-\)Gitter.
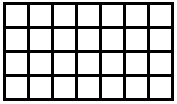
\(~4 \times 7~\) kann durch \(~m_1 \times m_2~\) ersetzt werden, mit den Teilern \(~m_1,~m_2~\) von \(~n~\). Es sollen alle Möglichkeiten zur Bildung dieser Gitter gezählt werden: Da \(~m_2 = n/m_1~\) gilt und \(~(m_1 \times m_2)-\)Gitter mit \(~(m_2 \times m_1)-\)Gittern identifiziert werden, durchläuft \(~m_1~\) die Hälfte der Teiler – allerdings nur wenn \(~n~\) keine Quadratzahl ist; ist \(~n~\) eine Quadratzahl, dann gibt es ein \(~(\sqrt{n} \times \sqrt{n})~-\)Gitter; dies ist der einzige Fall für eine ungerade Anzahl von Teilern. Wir bezeichnen die Anzahl der kartesischen 2D-Gitter mit \(~n~\) Quadraten durch \(~g_{aa}(n)~\) und erhalten:
\[\textbf{(3)}~~~g_{aa}(n)=\left\lceil \frac{\tau (n)}{2} \right\rceil\]
Bemerkungen:
\(\tau(n)~\) wurde in (2) angegeben.
\(\lceil~..\rceil\) liefert die kleinste ganze Zahl, die größer oder gleich dem Argument ist \(~~~\longrightarrow~~~g_{aa}(n)=(\tau(n)+1)/2~\), falls \(~n~\) ein Quadrat ist und \(~g_{aa}(n)=\tau(n)/2~\) sonst.
Mathematica:
\(g_{aa}(n)~\) erhält man mit Ceiling[Length[Divisors[n]]/2]
OEIS:
\(g_{aa}(n)~=~\)\(\text{A038548}(n)\)
Das nicht-kartesische Gitter im nächsten Bild enthält \(~n=15~\) Rechtecke und ist ein \(~(3 \times 5)-\)Gitter.
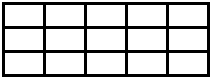
\(~3 \times 5~\) kann durch \(~m_1 \times m_2~\) ersetzt werden, mit den Teilern \(~m_1,~m_2~\) von \(~n~\). Aber im Gegensatz zu kartesischen Gittern können \(~(m_1 \times m_2)-\)Gitter nicht mit \(~(m_2 \times m_1)-\)Gittern identifiziert werden. Also durchläuft \(~m_1~\) alle Teiler. Wir bezeichnen die Anzahl der nicht-kartesischen 2D-Gitter mit \(~n~\) Rechtecken durch \(~g_{ab}(n)~\) und erhalten:
\(\textbf{(4)}~~~g_{ab}(n)=\tau (n)~\), siehe (2)
Kartesische 3D-Gitter (aaa-Gitter)
Das kartesische Gitter in Bild 3 enthält \(~n=84~\) Würfel und ist ein \(~(4 \times 7 \times 3)-\)Gitter.
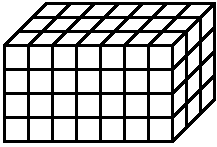
Bild 3 aaa-Gitter
Wie im vergleichbaren 2D-Fall werden \(~(m_1 \times m_2 \times m_3)-\)Gitter mit \(~(m_1 \times m_3 \times m_2)-\)Gittern identifiziert; ebenso für andere Permutationen der drei Teiler. Folglich suchen wir nach Teilern mit \(~m_1 \leq m_2 \leq m_3~\). Wir bezeichnen die Anzahl der kartesischen 3D-Gitter mit \(~n~\) Würfeln durch \(~g_{aaa}(n)~\). Eine Formel für \(~g_{aaa}(n)~\) ist nicht bekannt.
Mathematica:
\(g_{aaa}(n)~\) erhält man mit
b=0; d=Divisors[n]; r=Length[d];
Do[If[d[[h]] d[[i]] d[[j]]==n, b++], {h, r}, {i, h, r}, {j, i, r}];
b
OEIS:
\(g_{aaa}(n)~=~\)\(\text{A034836}(n)\)
aab-Gitter
Das nicht-kartesische \(~(4 \times 7 \times 2)-\)Gitter in Bild 4 ist ein aab-Gitter mit \(~n=56~\) kongruenten Quadern mit zwei verschiedenen Kantenlängen.
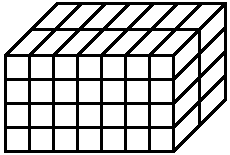
Bild 4 aab-Gitter
Ein naheliegender Weg zur Bestimmung der Anzahl der möglichen aab-Gitter ist die Aufsummierung aller kartesischen 2D-Gitter – die Vorderseite (mit den Quadraten) des großen Quaders in Bild 4 möge als Beispiel dienen. Mit "alle" sind die 2D-Gitter gemeint, die \(~m~\) Quadrate mit \(~m|n~\) enthalten (d.h. \(m~\) ist ein Teiler von \(~n\)). Wir bezeichnen die Anzahl der aab-Gitter mit \(~n~\) Quadern durch \(~g_{aab}(n)~\). Mit (3) erhalten wir:
\[\textbf{(5)}~~~g_{aab}(n)=\sum_{m|n} g_{aa}(m)=\sum_{m|n}~\left\lceil \frac{\tau (m)}{2} \right\rceil\]
Mathematica:
\(g_{aab}(n)~\) erhält man mit
d=Divisors[n]; r=Length[d];
Sum[Ceiling[Length[Divisors[d[[j]]]]/2],{j, r}]
OEIS:
\(g_{aab}(n)~=~\)\(\text{A140773}(n)\)
abc-Gitter
Das nicht-kartesische \(~(3 \times 5 \times 2)-\)Gitter in Bild 5 ist ein abc-Gitter mit \(~n=30~\) kongruenten Quadern mit drei verschiedenen Kantenlängen.
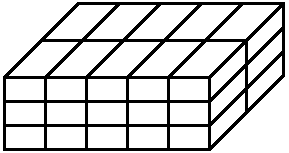
Bild 5 abc-Gitter
Wir bezeichnen die Anzahl der abc-Gitter mit \(~n~\) Quadern durch \(~g_{abc}(n)~\).
Es soll gezeigt werden, dass \(~g_{abc}(n)~\) gleich der Anzahl der Teiler der Teiler von \(~n~\) ist. Das bedeutet, dass wir für jeden Teiler \(~m~\) von \(~n~\) dessen Teileranzahl \(~\tau (m)~\) bestimmen und all diese Teileranzahlen zu \(~g_{abc}(n)~\) aufaddieren.
Man betrachte eine der Seitenflächen des großen Quaders in Bild 5, o.E. die Vorderseite mit \(~15~\) Rechtecken. Die Anzahl dieser Rechtecke muss ein Teiler von \(~n~\) sein, und jeder Teiler von \(~n~\) kommt dafür in Frage, da die betrachteten (Vorder-)Seiten nicht-kartesische 2D-Gitter sind; siehe die Erläuterungen zu (4). Sei \(~m~\) ein solcher Teiler. \(~m~\) steht dann für die Anzahl von Rechtecken in einem \(~(k \times m/k)-\)Gitter mit \(~k|m~\). Also erhalten wir für jeden Teiler \(~m~\) von \(~n~\) genau \(~\tau (m)~\) verschiedene abc-Gitter. Dies beweist unsere Behauptung.
Was eben gezeigt wurde, bedeutet, dass wir nur auf eine Seitenfläche des großen Quaders schauen müssen, denn die Anzahl \(~n/m~\) der "Ebenen dahinter" ist bereits eindeutig bestimmt durch die Anzahl \(~m~\) der Rechtecke auf der betrachteten Seitenfläche. \(~m~\) kann zu \(~k \cdot (m/k)~\) faktorisiert werden mit \(~k|m~\) (s.o.), um ein Rechteck für die Seitenfläche zu bilden. Wir erhalten auf diese Weise ein \(~(m_1 \times m_2 \times m_3)-\)Gitter mit \(~(m_1 \times m_2 \times m_3)=(k \times (m/k) \times (n/m))~\), wobei jede Permutation der \(~m_i~\) ein anderes Gitter liefert.
\(m|n~\) bedeutet \(~m=\prod_{i=1}^s p_i^{v_i}~\) with \(~0 \leq v_i \leq h_i~\), siehe (1), und jedes Tupel \(~(v_i)_{~i=1~..~s}~\) ergibt einen Teiler \(~m~\) von \(~n~\). \(~m~\) hat \(~\tau(m)=\prod_{i=1}^s~(1+v_i)~\) Teiler, siehe (2). Damit gilt:
\[g_{abc}(n)=\sum_{0\leq v_i \leq h_i}~\prod_{i=1}^s ~(1+v_i)=\sum_{v_1=0}^{h_1}~\sum_{v_2=0}^{h_2}~...\sum_{v_s=0}^{h_s}~\prod_{i=1}^s ~(1+v_i)=\sum_{v_1=0}^{h_1}(1+v_1) \sum_{v_2=0}^{h_2}(1+v_2)~...\sum_{v_s=0}^{h_s}(1+v_s)\]
\[\textbf{(6)}~~~g_{abc}(n)=\prod_{i=1}^s~\binom{2+h_i}{2}\]
Mathematica:
\(g_{abc}(n)~\) erhält man mit Length[Flatten[Divisors[Divisors[n]]]]
oder f=FactorInteger[n]; r=Length[f]; Product[Binomial[2+f[[m]][[2]],2],{m, r}]
OEIS:
\(g_{abc}(n)~=~\)\(\text{A007425}(n)\)
Kommentare sind willkommen.
Stand 2022-01-18
Inhalt Blog | voriger Eintrag | nächster Eintrag
Manfred Börgens | Zur Leitseite
 MB Matheblog # 17
MB Matheblog # 17 MB Matheblog # 17
MB Matheblog # 17 english version
english version





