Problem des Monats Dezember 2004

Zur diesjährigen Weihnachtsfeier will der Verein eine Tombola veranstalten. Der dreiköpfige Vereinsvorstand erklärt sich bereit, alle Gewinne zu stiften. Nieten soll es nicht geben. Der Vereinsvorsitzende bespricht sich mit den beiden anderen im Vorstand: "Wir brauchen mindestens 30 Gewinne, noch mehr wären natürlich sehr schön. Ich schlage vor, dass jeder von uns dreien die gleiche Anzahl von Gewinnen stiftet." Seinem Vorschlag wird gefolgt.

Bei der Feier kaufen auch die drei Vorstandsmitglieder je ein Los. Wie groß ist die Wahrscheinlichkeit (auf volle Prozent gerundet), dass keiner von ihnen einen Gewinn erhält, den er selbst gestiftet hat?

Lösung

Es gibt eine schnelle Lösung - eher intuitiv als mathematisch präzise -, die darauf baut, dass es sich um eine sinnvolle Problemstellung handelt. In diesem Fall hängt nämlich das Ergebnis offenbar nicht von der Anzahl der Gewinne ab, falls es genügend viele davon gibt (mindestens 30). Für "sehr viele" Gewinne ist die Wahrscheinlichkeit für jedes einzelne Vorstandsmitglied näherungsweise  2/3 , einen "fremden" Gewinn zu ziehen. Dass alle drei einen fremden Gewinn erhalten, hat also die Wahrscheinlichkeit  (2/3)³ = 0.296... , also gerundet 30 %.

Eine genauere Analyse zeigt, dass es 8 Fälle gibt, wie die Vorstandsmitglieder A, B, C fremde Gewinne erhalten können (es wird jeweils an 1./ 2./ 3. Stelle die Quelle des Gewinns für A / B / C genannt):

B A A
B A B
B C A
B C B
C A A
C A B
C C A
C C B

Wahrscheinlichkeit für BCA bzw. CAB:
Der Einfachheit halber stellen wir uns vor, dass zuerst A in die Lostrommel greift, dann B und zuletzt C. Die Anzahl aller verfügbaren Gewinne soll  3n  betragen (d.h. jedes Vorstandsmitglied hat  n  Gewinne gestiftet,  n > 9 ).

Für A:  n  günstige unter  3n  möglichen Gewinnen.
Für B:  n  günstige unter  3n - 1  möglichen Gewinnen.
Für C:  n  günstige unter  3n - 2  möglichen Gewinnen.

Für BCA bzw. CAB erhalten wir somit jeweils die Wahrscheinlichkeit  n² / 3(3n - 1)(3n - 2) . Auf dieses Ergebnis kann man auch auf einem anderen Weg kommen: Aus  3n  Gewinnen sind  3  auszuwählen, unter Berücksichtigung der Reihenfolge. Dafür braucht man die kombinatorische Formel für Variationen ohne Wiederholung (geordnete Stichproben ohne Zurücklegen): Es gibt  (3n)! / (3n - 3)!  Möglichkeiten. Unter diesen sind für BCA bzw. CAB jeweils  n³  Möglichkeiten. Durch Kürzen erhält man wieder die Wahrscheinlichkeit  n² / 3(3n - 1)(3n - 2) .

Wahrscheinlichkeit für die anderen 6 Fälle BAA, BAB usw.:
Hier kommt immer ein Buchstabe doppelt vor. Argumentiert man wie zuvor, so erhält man z.B. für BAA:

Für A:  n  günstige unter  3n  möglichen Gewinnen.
Für B:  n  günstige unter  3n - 1  möglichen Gewinnen.
Für C:  n - 1  günstige unter  3n - 2  möglichen Gewinnen.

Dies gilt für alle 6 Fälle mit doppelten Buchstaben (bei den beiden letzten stehen  n - 1  günstige für B und  n  günstige für C). Jeder einzelne dieser Fälle hat also die Wahrscheinlichkeit  n(n - 1) / 3(3n - 1)(3n - 2) . Auch auf dieses Ergebnis kann man über Variationen kommen: Unter den  (3n)! / (3n - 3)!  Möglichkeiten gibt es hier für jeden der 6 Fälle jeweils  n²(n - 1)  Möglichkeiten. Durch Kürzen erhält man wieder die Wahrscheinlichkeit  n(n - 1) / 3(3n - 1)(3n - 2).

Gesamtwahrscheinlichkeit
In der Liste der 8 Fälle kamen drei verschiedene Buchstaben zweimal vor, zwei gleiche Buchstaben sechsmal. Also ist die Gesamtwahrscheinlichkeit für alle 8 Fälle:



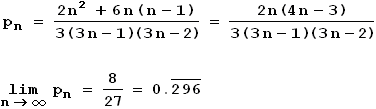
Man berechnet  p₁₀ = 0.3038  (gerundet), was ebenso wie der Grenzwert auf volle Prozent gerundet 30 % ergibt. Es ist noch zu begründen, dass dies auch für alle  p_n  mit  n > 10  gilt. Es reicht zu zeigen, dass die  p_n  für  n > 9  monoton gegen den Grenzwert fallen: Die Funktion  f(x) = 2x(4x - 3) / 3(3x - 1)(3x - 2)  hat die Ableitung  f'(x) = (-2/3)·(9x² - 16x + 6) / (3x - 1)²(3x - 2)² . Die Nullstellen des Nenners sind kleiner als  1 , also für unser Problem ohne Bedeutung. Die Nullstellen des Zählers liegen grob gerundet bei  0.54  und  1.24 .  9x² - 16x + 6  ist also rechts von der zweiten Nullstelle positiv,  f'(x)  somit negativ, dort fällt also die Funktion streng monoton. Folglich fallen die  p_n  streng monoton für alle  n > 1 . Hier ist eine Übersicht der  p_n :

p₁ = 1/3      (die 6 Fälle mit zwei gleichen Buchstaben in der Liste oben haben alle die Wahrscheinlichkeit  0 )
p₂ = 1/3
p₃ = 9/28 = 0.3214      (gerundet)
...
...
p₈ = 0.3057      (gerundet)
p₉ = 0.3046      (gerundet)
p₁₀ = 0.3038      (gerundet)
p₁₁ = 0.3031      (gerundet)
...
Grenzwert:  8/27 = 0.296296...


Die Wahrscheinlichkeit, dass kein Mitglied des Vereinsvorstands einen selbst gestifteten Gewinn erhält, beträgt (nur) 30 %.