Problem des Monats November 2004

Unter den zahlreichen Varianten der Nim-Spiele ist die folgende wohl etwas weniger bekannt, dafür aber besonders reizvoll. Zunächst wird ein konkretes Spiel formuliert; es ist die beste Strategie für die Spieler herauszufinden.

Auf dem Tisch liegen 17 Spielsteine. Zwei Spieler nehmen immer abwechselnd Steine fort, wobei sie sich jedesmal neu entscheiden können, ob sie einen Stein, zwei Steine oder drei Steine nehmen. Gewonnen hat derjenige Spieler, der am Ende eine ungerade Anzahl von Steinen hat.

Da es sich um ein Spiel mit nur endlich vielen Möglichkeiten handelt, das außerdem keine Unentschieden erlaubt, kann es nur zwei Möglichkeiten geben, wenn beide Spieler (der "Anziehende" und der "Nachziehende") keinen Fehler machen: Entweder gewinnt immer der Anziehende oder immer der Nachziehende. Allerdings sollte man sich auch auf die Situation einstellen, dass der Gegner nicht fehlerfrei spielt, d.h. auch für alle Zwischenpositionen (wenn also weniger als 17 Spielsteine auf dem Tisch liegen) sollte man den optimalen Zug kennen.

Für dieses Spiel lautet die naheliegende Verallgemeinerung:

Auf dem Tisch liegen  n_o  Spielsteine. Zwei Spieler nehmen immer abwechselnd maximal  m  Steine fort. Gewonnen hat derjenige Spieler, der am Ende eine ungerade Anzahl von Steinen hat. Klar ist, dass  n_o  ungerade sein muss.

Lösung

Wir beginnen mit dem konkreten Problem:  m = 3 . Da das optimale Verhalten der Spieler beschrieben werden muss, wenn noch  n  Steine auf dem Tisch liegen, liegt es nahe, mit kleinen  n  anzufangen. Es soll jeweils beschrieben werden, welcher Spieler gewinnt, wenn er sich optimal verhält, und was er dafür tun muss. Dass  n_o = 17  ist, soll zunächst keine Rolle spielen, d.h. es soll eine allgemeine beste Strategie für beliebige  n_o  gefunden werden.

n = 0
Dies ist das Ende des Spiels. Nach der Spielregel gewinnt derjenige Spieler, der eine ungerade Anzahl von Steinen hat.

n = 1
Die Spieler haben entweder beide eine ungerade oder beide eine gerade Anzahl von Steinen. Also gewinnt der Spieler, der am Zug ist (der "Anziehende") genau dann, wenn beide eine gerade Anzahl haben.

n = 2
Es gewinnt der Anziehende. Hat er eine ungerade Anzahl von Steinen, nimmt er 2 Steine weg, und erreicht  n = 0 . Hat er eine gerade Anzahl von Steinen, nimmt er einen Stein weg, und erreicht  n = 1 ; sein Gegner, der dann am Zug ist, verliert, weil beide Spieler ungerade viele Steine haben.

n = 3
Es gewinnt der Anziehende. Hat er eine gerade Anzahl von Steinen, nimmt er 3 Steine weg, und erreicht  n = 0 . Hat er eine ungerade Anzahl von Steinen, nimmt er 2 Steine weg, und erreicht  n = 1 ; sein Gegner, der dann am Zug ist, verliert, weil beide Spieler ungerade viele Steine haben.

n = 4
Ein Spieler hat eine ungerade Anzahl von Steinen, der andere eine gerade. Es gewinnt der Spieler mit der geraden Anzahl. Ist er der Anziehende, nimmt er 3 Steine und erreicht  n = 1 ; sein Gegner, der dann am Zug ist, verliert, weil beide Spieler ungerade viele Steine haben. Ist der Spieler mit der geraden Anzahl von Steinen dagegen der Nachziehende, so gewinnt er ebenfalls, denn er ist beim nächsten Zug der Anziehende bei  n = 3, n = 2  oder  n = 1 , was jeweils günstig für ihn ist.

n = 5
Die Spieler haben entweder beide eine ungerade oder beide eine gerade Anzahl von Steinen. Es gewinnt der Anziehende genau dann, wenn beide eine ungerade Anzahl haben. In diesem Fall nimmt er einen Stein und erreicht  n = 4 . Haben dagegen beide eine gerade Anzahl, so kann der Anziehende nur  n = 4, n = 3  oder  n = 2  erreichen, und der Gegner gewinnt, weil er dann der Anziehende ist.

n = 6
Es gewinnt der Anziehende. Hat er eine ungerade Anzahl von Steinen, nimmt er einen Stein weg, und erreicht  n = 5 . Hat er eine gerade Anzahl von Steinen, nimmt er 2 Steine weg, und erreicht  n = 4 .

n = 7
Es gewinnt der Anziehende. Hat er eine ungerade Anzahl von Steinen, nimmt er 3 Steine weg, und erreicht  n = 4 . Hat er eine gerade Anzahl von Steinen, nimmt er 2 Steine weg, und erreicht  n = 5 .

n = 8
Ein Spieler hat eine ungerade Anzahl von Steinen, der andere eine gerade. Es gewinnt der Spieler mit der ungeraden Anzahl. Ist er der Anziehende, nimmt er 3 Steine und erreicht  n = 5 . Ist der Spieler mit der ungeraden Anzahl dagegen der Nachziehende, so gewinnt er ebenfalls, denn er ist beim nächsten Zug der Anziehende bei  n = 7, n = 6  oder  n = 5 , was jeweils günstig für ihn ist.

n = 9
Die Spieler haben entweder beide eine ungerade oder beide eine gerade Anzahl von Steinen. Es gewinnt der Anziehende genau dann, wenn beide eine gerade Anzahl haben. In diesem Fall nimmt er einen Stein und erreicht  n = 8 . Haben dagegen beide eine ungerade Anzahl, so kann der Anziehende nur  n = 8, n = 7  oder  n = 6  erreichen, und der Gegner gewinnt, weil er dann der Anziehende ist.

n = 10
Es gewinnt der Anziehende  -  analog  n = 2 .

n = 11
Es gewinnt der Anziehende  -  analog  n = 3 .

n = 12
Ein Spieler hat eine ungerade Anzahl von Steinen, der andere eine gerade. Es gewinnt der Spieler mit der geraden Anzahl  -  analog  n = 4 .

n = 13
Die Spieler haben entweder beide eine ungerade oder beide eine gerade Anzahl von Steinen. Es gewinnt der Anziehende genau dann, wenn beide eine ungerade Anzahl haben  -  analog  n = 5 .

n = 14
Es gewinnt der Anziehende  -  analog  n = 6 .

n = 15
Es gewinnt der Anziehende  -  analog  n = 7 .

n = 16
Ein Spieler hat eine ungerade Anzahl von Steinen, der andere eine gerade. Es gewinnt der Spieler mit der ungeraden Anzahl  -  analog  n = 8 .

n = 17
Die Spieler haben entweder beide eine ungerade oder beide eine gerade Anzahl von Steinen. Es gewinnt der Anziehende genau dann, wenn beide eine gerade Anzahl haben  -  analog  n = 9 .


Hier wollen wir innehalten. Erstens erkennt man eine Systematik (nämlich eine Wiederholung von "Blöcken" der Länge 8), die in Tabelle 1 noch deutlicher wird und die weiter unten noch genauer behandelt wird. Zweitens ist das ursprüngliche Problem  n_o = 17  und  m = 3  damit gelöst, denn beide Spieler haben zu Beginn 0 Steine, also eine gerade Anzahl. Für dieses spezielle Problem kann man die Situation bei  n = 17  und  n = 16  neu formulieren:

n = n_o = 17
Der Anziehende gewinnt, indem er einen Stein nimmt und  n = 16  erreicht.

n = 16
Der Nachziehende gewinnt. Wenn der Anziehende einen Stein oder 2 Steine nimmt, gelangt man zu  n = 15  bzw.  n = 14 . Nimmt er 3 Steine, so haben bei  n = 13  beide Spieler eine ungerade Anzahl von Steinen.

Für jede Anzahl von Steinen, die noch auf dem Tisch liegen, lassen sich nun das optimale Verhalten des Spielers, der am Zug ist, und die Gewinnaussichten für beide Spieler bei optimalem Spiel tabellarisch darstellen:



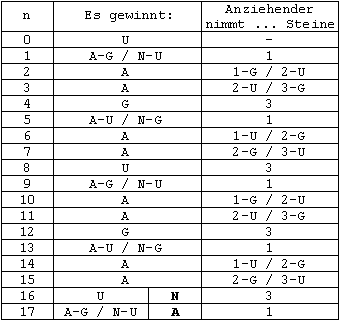
Tabelle 1    n_o = 17  und  m = 3 

Legende:
A     Anziehender
N     Nachziehender
U     ungerade Anzahl Spielsteine
G     gerade Anzahl Spielsteine

In Tabelle 1 bedeutet also  N - G  "Nachziehender gewinnt genau dann, wenn er eine gerade Anzahl Steine hat".  3 - U  bedeutet "Anziehender nimmt 3 Steine, falls er eine ungerade Anzahl Steine hat". Die anderen Zeichenkombinationen sind analog definiert.

Bei  n = 16  und  n = 17  ist in Tabelle 1 sowohl die Systematik von  n = 0  bis  n = 15  fortgeführt worden als auch (fett) eingetragen, was aus  n_o = 17  direkt folgt.



Allgemeines Problem für beliebige ungerade  n_o  und  m > 1

m = 3

Tabelle 1 legt eine Systematik mit 8-er Blöcken nahe, die in Tabelle 2 dargestellt ist. Dort ist  k = 0, 1, 2, ... ; von einem  n_o = 8k + j  ausgehend liest man die Tabelle von unten nach oben.


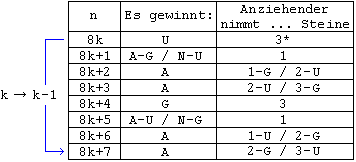
            * entfällt für  k = 0

Tabelle 2    m = 3


Dass Tabelle 2 die optimale Strategie für  m = 3  beschreibt, zeigt man induktiv. Für  k = 0  und  k = 1  ist dies bereits durch Tabelle 1 gezeigt. Setzt man nun die Richtigkeit für ein  k  voraus, so läuft der Induktionsschritt ganz analog zu der Argumentation am Anfang dieser Lösung. Der Vollständigkeit halber wird sie hier nochmal aufgeführt:

n = 8(k + 1)
Ein Spieler hat eine ungerade Anzahl von Steinen, der andere eine gerade. Es gewinnt der Spieler mit der ungeraden Anzahl. Ist er der Anziehende, nimmt er 3 Steine und erreicht  n = 8k + 5 ; also gewinnt er, denn dann ist er der Nachziehende mit einer geraden Anzahl von Steinen. Ist der Spieler mit der ungeraden Anzahl dagegen der Nachziehende, so gewinnt er ebenfalls, denn er ist beim nächsten Zug der Anziehende bei  n = 8k + 7, n = 8k + 6  oder  n = 8k + 5 , was jeweils günstig für ihn ist.

n = 8(k + 1) + 1
Die Spieler haben entweder beide eine ungerade oder beide eine gerade Anzahl von Steinen. Es gewinnt der Anziehende genau dann, wenn beide eine gerade Anzahl haben. In diesem Fall nimmt er einen Stein und erreicht  n = 8(k + 1) . Haben dagegen beide eine ungerade Anzahl, so kann der Anziehende nur  n = 8(k + 1)  (dann hat er eine gerade Anzahl),  n = 8k + 7  oder  n = 8k + 6  erreichen, und der Gegner gewinnt, weil er dann der Anziehende ist.

n = 8(k + 1) + 2
Es gewinnt der Anziehende. Hat er eine ungerade Anzahl von Steinen, nimmt er 2 Steine weg, und erreicht  n = 8(k + 1) . Hat er eine gerade Anzahl von Steinen, nimmt er einen Stein weg, und erreicht  n = 8(k + 1) + 1 ; sein Gegner, der dann am Zug ist, verliert, weil beide Spieler ungerade viele Steine haben.

n = 8(k + 1) + 3
Es gewinnt der Anziehende. Hat er eine gerade Anzahl von Steinen, nimmt er 3 Steine weg, und erreicht  n = 8(k + 1) . Hat er eine ungerade Anzahl von Steinen, nimmt er 2 Steine weg, und erreicht  n = 8(k + 1) + 1 ; sein Gegner, der dann am Zug ist, verliert, weil beide Spieler ungerade viele Steine haben.

n = 8(k + 1) + 4
Ein Spieler hat eine ungerade Anzahl von Steinen, der andere eine gerade. Es gewinnt der Spieler mit der geraden Anzahl. Ist er der Anziehende, nimmt er 3 Steine und erreicht  n = 8(k + 1) + 1 ; sein Gegner, der dann am Zug ist, verliert, weil beide Spieler ungerade viele Steine haben. Ist der Spieler mit der geraden Anzahl von Steinen dagegen der Nachziehende, so gewinnt er ebenfalls, denn er ist beim nächsten Zug der Anziehende bei  n = 8(k + 1) + 3, n = 8(k + 1) + 2  oder  n = 8(k + 1) + 1 , was jeweils günstig für ihn ist.

n = 8(k + 1) + 5
Die Spieler haben entweder beide eine ungerade oder beide eine gerade Anzahl von Steinen. Es gewinnt der Anziehende genau dann, wenn beide eine ungerade Anzahl haben. In diesem Fall nimmt er einen Stein und erreicht  n = 8(k + 1) + 4 . Haben dagegen beide eine gerade Anzahl, so kann der Anziehende nur  n = 8(k + 1) + 4, n = 8(k + 1) + 3  oder  n = 8(k + 1) + 2  erreichen, und der Gegner gewinnt, weil er dann der Anziehende ist.

n = 8(k + 1) + 6
Es gewinnt der Anziehende. Hat er eine ungerade Anzahl von Steinen, nimmt er einen Stein weg, und erreicht  n = 8(k + 1) + 5 . Hat er eine gerade Anzahl von Steinen, nimmt er 2 Steine weg, und erreicht  n = 8(k + 1) + 4 .

n = 8(k + 1) + 7
Es gewinnt der Anziehende. Hat er eine ungerade Anzahl von Steinen, nimmt er 3 Steine weg, und erreicht  n = 8(k + 1) + 4 . Hat er eine gerade Anzahl von Steinen, nimmt er 2 Steine weg, und erreicht  n = 8(k + 1) + 5 .

Legt man zu Beginn des Spiels ein (ungerades)  n_o  fest, so zeigt Tabelle 1: Der Nachziehende gewinnt nur bei  n_o = 8k + 5 , dagegen der Anziehende bei  n_o = 8k + 1  (z.B.  n_o = 17 ),  n_o = 8k + 3, n_o = 8k + 7 .



m = 5

Wenn man verschiedene  m  durchprobiert, sieht man sehr schnell, dass die Darstellung der optimalen Strategie für gerade und ungerade  m  unterschiedlich ausfällt. Deshalb sollen nach  m = 3  zunächst die anderen ungeraden  m  behandelt werden, statt der eigentlich näher liegenden  m = 2  und  m = 4 .

Der Gedankengang für  m = 5, m = 7  usw. ist dem für  m = 3  sehr ähnlich. Man kommt für  m = 5  auf die folgende Tabelle 3, die sich analog zu  m = 3  begründen lässt:


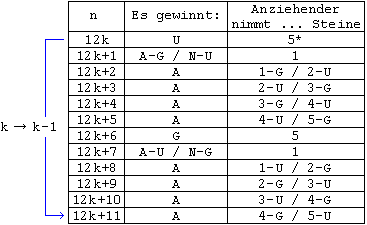
            * entfällt für  k = 0

Tabelle 3    m = 5


Der Nachziehende gewinnt nur bei  n_o = 12k + 7 , dagegen der Anziehende bei allen anderen ungeraden  n_o .


m  ungerade

Ausgehend von  m = 3  und  m = 5  lässt sich nun leicht der allgemeine Fall für ungerade  m  behandeln (Beweis analog  m = 3 ), siehe Tabelle 4. Die Länge der "Blöcke" (Periodenlänge) ist  2m + 2 . Sie zerfallen in zwei Teilblöcke der Länge  m + 1 , jeweils beginnend mit zwei  n , bei denen der Gewinner davon abhängt, ob der Anziehende eine ungerade oder gerade Anzahl Steine hat. Dann folgen in jedem Teilblock  m - 1 "A" .


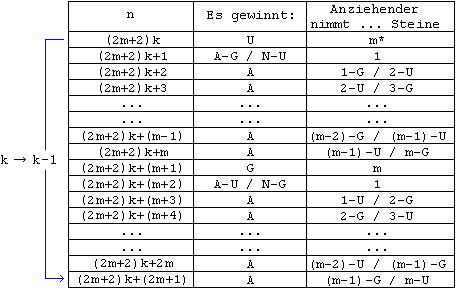
            * entfällt für  k = 0

Tabelle 4    m  ungerade


Der Nachziehende gewinnt nur bei  n_o = (2m + 2)k + (m + 2) , dagegen der Anziehende bei allen anderen  n_o .



m = 2

Mit Überlegungen analog zu  m = 3  erhält man Tabelle 5:



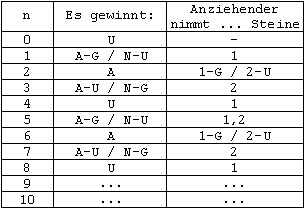
Tabelle 5    m = 2

Hier ist die Periodenlänge 4, und man sieht, dass die Struktur der Tabelle sich von der für ungerade  m  unterscheidet. Insbesondere taucht hier erstmals der Fall auf, dass der Anziehende auf zwei verschiedenen Wegen zum Erfolg kommt, nämlich bei  n = 5 . In Tabelle 6 ist ein allgemeiner Block dargestellt:


            * entfällt für  k = 0
            ** 2 entfällt für  k = 0

Tabelle 6    m = 2


Der Anziehende gewinnt bei  n_o = 4k + 1 , der Nachziehende bei  n_o = 4k + 3 .



m = 4

Aufgrund der Analogie zu  m = 2  soll sofort die Tabelle mit einem Periodenblock gezeigt werden:


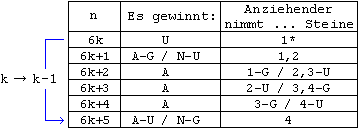
            bei Einträgen in der Form  a,b  in der letzten Spalte entfällt  b  für  k = 0
            * entfällt für  k = 0

Tabelle 7    m = 4

Hier ist die Periodenlänge 6. Der Nachziehende gewinnt nur bei  n_o = 6k + 5 , der Anziehende bei  n_o = 6k + 1  und  n_o = 6k + 3 .


m  gerade

Ausgehend von  m = 2  und  m = 4  ergibt sich nun der allgemeine Fall für gerade  m  (Beweis analog  m = 3 ), siehe Tabelle 8 für  m > 2 . Die Periodenlänge ist  m + 2 . Im Gegensatz zu ungeraden  m  gibt es hier keine Unterteilung in zwei ähnliche Teilblöcke. Jeweils  m - 1 "A"  wechseln sich ab mit drei  n , bei denen der Gewinner davon abhängt, ob der Anziehende eine ungerade oder gerade Anzahl Steine hat.


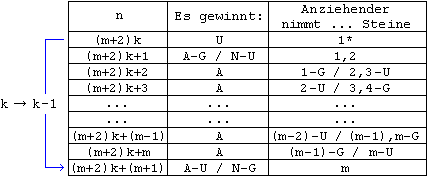
            bei Einträgen in der Form  a,b  in der letzten Spalte entfällt  b  für  k = 0
            * entfällt für  k = 0

Tabelle 8    m > 2  gerade

Der Nachziehende gewinnt nur bei  n_o = (m + 2)k + (m + 1) , der Anziehende bei allen anderen ungeraden  n_o .



Zusammenfassung



Tabelle 9


Was bedeutet die Wahrscheinlichkeit in der letzten Spalte von Tabelle 9 ? Man könnte  n_o  vor dem Spiel unter Berücksichtigung der Periodenlänge  p  auslosen, indem man  n_o = pk + j  ansetzt,  k  auf beliebige Weise bestimmt und  j  unter den Zahlen  0, 1, ... , p - 1  auslost.