| Manfred Börgens Mathematische Probleme # 39 |
Liste aller Probleme mit Lösungen voriges Problem nächstes Problem |
zur Leitseite |
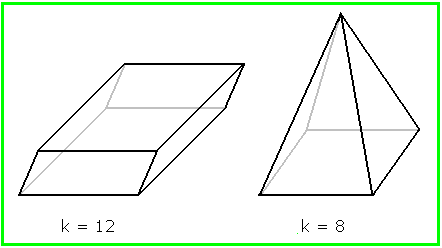
Ein Polyeder ist ein Körper mit ebenen Grenzflächen. Polyeder wurden auf diesen Seiten schon behandelt: Problem des Monats April 2003 und Briefmarke des Monats November 2000 . Es soll geklärt werden, wieviele Kanten ein Polyeder haben kann. Hier sehen wir zwei Polyeder mit 12 bzw. 8 Kanten:

Welche Kantenzahlen können vorkommen ?
Die Euler'sche Polyederformel kann hier nützlich sein (ist aber nicht unbedingt erforderlich): Werden mit e, f, k die Anzahlen der Ecken, Flächen und Kanten eines Polyeders bezeichnet, so gilt e + f = k + 2 .
Sei k die Anzahl der Kanten eines Polyeders.
Kein Polyeder hat k < 6 Kanten.
Wählt man eine beliebige Fläche des Polyeders aus, so hat diese mindestens drei Ecken bzw. Kanten. Von diesen Ecken muss jeweils mindestens eine weitere Kante ausgehen, da an jeder Ecke mindestens drei Flächen zusammenstoßen. Man kommt so auf ein Minimum von k = 6 Kanten.
Ist k mindestens 6 und eine gerade Zahl, so gibt es ein Polyeder mit k Kanten.
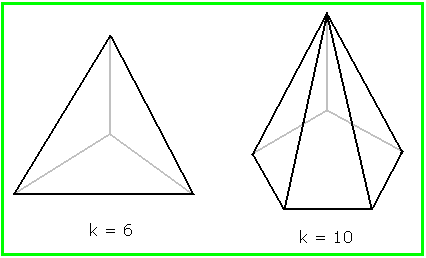
Eine Pyramide mit einem (k/2)-Eck als Grundfläche hat k Kanten. Die folgenden Bilder zeigen Beispiele für k = 6 (Tetraeder) und k = 10 .
Ist k mindestens 9 und eine ungerade Zahl, so gibt es ein Polyeder mit k Kanten.
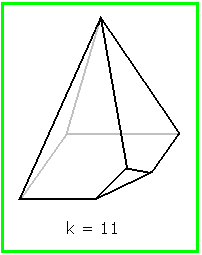
Schneidet man von den Pyramiden aus dem vorigen Abschnitt eine Ecke an der Grundfläche ab, so erhöht sich die Kantenzahl k um 3 . Aus Polyedern mit 6, 8, 10 ... Kanten werden dann Polyeder mit 9, 11, 13 ... Kanten. Das folgende Bild zeigt das Beispiel für k = 11 .
Es gibt kein Polyeder mit k = 7 Kanten.
Der Beweis für konvexe Polyeder lässt sich mit der Euler'schen Polyederformel führen: Für k = 7 wäre dann e + f = 9 , also e = 4 oder f = 4 . Durch e = 4 wird ein Tetraeder bestimmt, aber dieses hat k = 6 Kanten. Ist f = 4 , so muss jede der vier Flächen ein Dreieck sein, da von den Kanten nur drei weitere Flächen ausgehen können. Also erhält man wieder ein Tetraeder. -
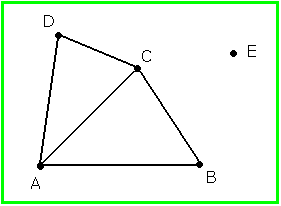
Man kommt auch ohne die Euler'sche Polyederformel aus: Ein Polyeder mit k = 7 Kanten kann nur Dreiecke als Begrenzungsflächen haben, da an jeder Ecke mindestens drei Kanten zusammenstoßen (d.h. ein n -Eck bringt mindestens 2n Kanten mit sich). Im folgenden Bild sind zwei dieser Dreiecke skizziert. Außer den Ecken A, B, C, D muss es noch mindestens eine weitere Ecke E geben, da sonst B und D verbunden werden müssten und so wieder ein Tetraeder entstehen würde. Von E gehen aber mindestens drei Kanten aus, so dass k > 7 wäre, im Widerspruch zur Annahme.
So ist bewiesen:
Für alle natürlichen Zahlen k mit Ausnahme von 1, 2, 3, 4, 5 und 7 gibt es Polyeder mit k Kanten.