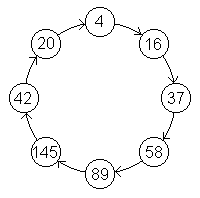
So führt etwa der Startwert 144 auf die Zahl 37; ab dort ist dann die Folge zyklisch:
| Manfred Börgens Mathematische Probleme # 19 |
Liste aller Probleme mit Lösungen voriges Problem nächstes Problem |
zur Leitseite |
Das folgende Problem lässt sich wohl nur lösen, indem man ein kleines Programm schreibt. Es soll eine Zahlenfolge mit dem folgenden Anfang berechnet werden:
223, 17, 50, 25, 29, 85, 89, ...
Denken Sie erst nach, ehe Sie weiterlesen, vielleicht erkennen Sie das Bildungsgesetz der Folge.
Die eigentliche Aufgabe besteht aber nicht darin, das Bildungsgesetz herauszufinden, deshalb wird es hier sofort verraten: Der Startwert ist beliebig (wir wollen uns aber auf natürliche Zahlen unter 1000 beschränken); jede weitere Zahl ist dann die Summe der Quadrate der einzelnen Ziffern ihres Vorgängers.
Durch diese Regel bleibt die Folge immer im Bereich der maximal dreistelligen natürlichen Zahlen. Deshalb ist klar, dass bei jedem Startwert nach der Berechnung einiger (evtl. vieler) Folgenglieder eine Zahl erscheinen muss, die schon einmal vorgekommen ist, und dann kann man aufhören, weil sich eine zyklische Wiederholung von Folgengliedern einstellt.
Hobby-Programmierer (möglicherweise auch Profis) haben jetzt vielleicht Spaß daran, etwas über die Eigenschaften dieser merkwürdigen Folge herauszufinden:
1.
Falls eine Folge bei der 1 angelangt ist, folgen nur noch Einsen nach, z.B.
973, 139, 91, 82, 68, 100, 1, 1, 1, ...
Gibt es außer der 1 noch weitere Zahlen, die auf sich selbst folgen?
2.
Welche anderen Wiederholungsmuster treten noch auf außer
1, 1, 1, ...
..., 10, 1, 1, 1, ...
..., 100, 1, 1, 1, ... ?
3.
Wegen 9 2 + 9 2 + 9 2 = 243 sind alle Folgenglieder außer dem Startwert kleiner als 244. Welches ist die höchste Zahl, die mehr als einmal in der Folge vorkommen kann?
4.
Einige Folgen münden sehr schnell in eine Wiederholung:
13, 10, 1, 1, 1, ...
Andere brauchen viel länger; probieren Sie z.B. den Startwert 121.
Wie lang ist der längste "Weg" einer Folge, bis eine Wiederholung auftritt?
5.
Welche "Wiederholungszahl" wird am häufigsten erreicht?
6.
Stellen Sie die möglichen Wiederholungsmuster zusammen mit den auftretenden Weglängen bis zur ersten Wiederholung übersichtlich dar.
7.
Was ändert sich, wenn beliebig große Startwerte zugelassen werden?
Probieren Sie einige der 999 möglichen Startwerte aus und beobachten Sie, was geschieht!
Sehr schnell stellt sich eine Vermutung ein: Entweder mündet die Folge in eine 1 und besteht ab da nur noch aus Einsen, oder sie mündet in den folgenden Zyklus ein:

So führt etwa der Startwert 144 auf die Zahl 37; ab dort ist dann die Folge zyklisch:
144, 33, 18, 65, 61, 37, 58, 89, 145, 42, 20, 4, 16, 37, ...
Diese Vermutung lässt sich nun schnell durch ein Programm überprüfen, das alle Startwerte durchgeht. Ein Zwischenergebnis ist dann, dass 142 Startwerte auf die 1 führen und 857 Startwerte auf den obigen 8-Zyklus. Eine genauere Aufteilung enthält die folgende Tabelle:
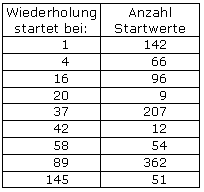
Nur die 9 Zahlen in der linken Tabellenspalte können also wiederholt in einer Folge vorkommen, alle anderen nur einmal. Ein systematisches Vorgehen kann nun für jeden Startwert bestimmen, in welche der 9 "Wiederholungszahlen" die Folge einmündet und wie viele Schritte dafür benötigt werden:
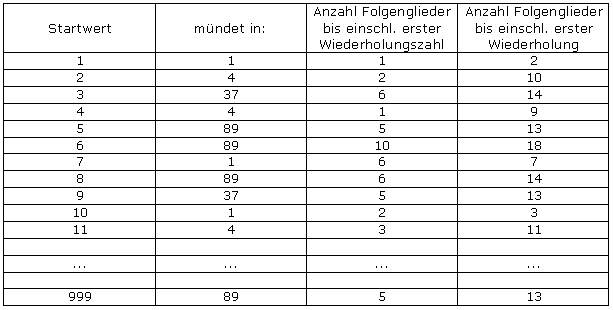
Mit dieser Tabelle lässt sich nun maschinell abzählen, wie oft die einzelnen Anzahlen in den beiden letzten Spalten für die 9 Wiederholungszahlen (2. Spalte) vorkommen. Diese Zählung ergibt:
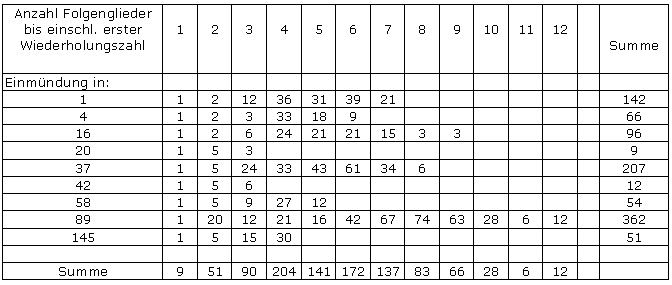
Die 999 möglichen Startwerte führen also auf nur 57 verschiedene Konstellationen (ausgefüllte Tabellenfelder).
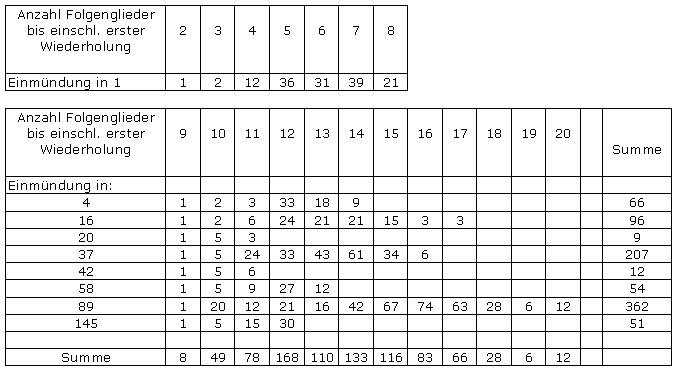
Man sieht, dass alle Folgenlängen von 2 bis 20 (und nur diese) bis zur ersten Wiederholung vorkommen.
Nun können alle Fragen aus der Aufgabenstellung beantwortet werden:
1. Nein.
2. Nur das zyklische Muster aus dem Bild oben kommt vor; jeweils mehrere Startwerte führen auf jede der Zahlen in diesem Muster.
3. 145
4. 20 (kommt nach der letzten Tabelle 12mal vor, z.B. beim Startwert 269)
5. 89
6. Siehe letzte drei Tabellen.
7. Die Folge mündet für jeden, beliebig großen Startwert in die
1-Folge oder in den 8-Zyklus ein. 4-stellige bis 12-stellige Startwerte führen
direkt im ersten Schritt auf eine 3-stellige Zahl; für größere Startwerte
kann mit jeder zusätzlichen Stelle des Startwerts maximal 81 beim Folgewert hinzukommen, wodurch sich dessen Stellen um maximal eine vermehren können (also führen 13-stellige Startwerte auf maximal 4-stellige Folgewerte usw.).
Kategorie: Zahlen und Zahlsysteme, Berechnung von π