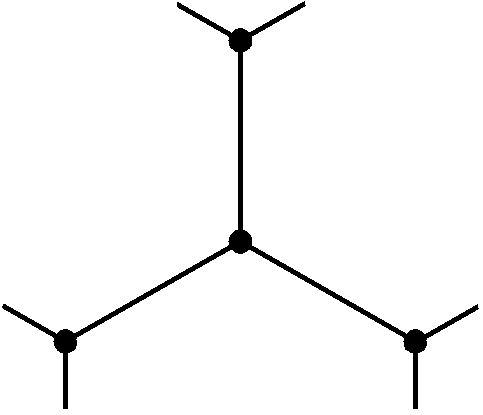
Ein Dorf hat n Häuser. Von jedem Haus gelangt man zu genau drei anderen Häusern auf einem direkten Weg, also ohne dass ein Haus dazwischen liegt. Alle diese Wege sind geradlinig, von gleicher Länge und überschneidungsfrei. Andere Wege gibt es in diesem Dorf nicht.
- Für welche n ist das möglich?
- Geben Sie einen "Beweis ohne Worte" für die möglichen n , indem Sie die Dörfer zeichnen.
Es liegt nahe, das Dorf als Graph aufzuzeichnen, mit den Häusern als Knoten und den Wegen als Kanten. Man stellt dann schnell fest, dass die Bedingung "gleich lange Wege" die meisten Schwierigkeiten bereitet.
— Ein Tipp kann abgerufen werden, indem der Rest dieser Zeile markiert wird: Für große n zeichnen Sie den Graph in Gestalt einer Strickleiter; finden Sie dann eine geeignete "Verknotung" an den Enden.
- Was ändert sich bei der Menge der möglichen n , wenn die Bedingung "kreuzungsfrei" aufgehoben wird?
- Was ändert sich bei der Menge der möglichen n , wenn die Bedingung "gleich lange Wege" aufgehoben wird?