Ein Dorf mit vielen Wegen           Die Lösung steht im unteren Teil der Seite. Ein Dorf hat  n  Häuser. Von jedem Haus gelangt man zu genau drei anderen Häusern auf einem direkten Weg, also ohne dass ein Haus dazwischen liegt. Alle diese Wege sind geradlinig, von gleicher Länge und überschneidungsfrei. Andere Wege gibt es in diesem Dorf nicht.  Für welche  n  ist das möglich?  Geben Sie einen "Beweis ohne Worte" für die möglichen  n , indem Sie die Dörfer zeichnen. Es liegt nahe, das Dorf als Graph aufzuzeichnen, mit den Häusern als Knoten und den Wegen als Kanten. Man stellt dann schnell fest, dass die Bedingung "gleich lange Wege" die meisten Schwierigkeiten bereitet. —   Ein Tipp kann abgerufen werden, indem der Rest dieser Zeile markiert wird: Für große  n  zeichnen Sie den Graph in Gestalt einer Strickleiter; finden Sie dann eine geeignete "Verknotung" an den Enden.  Was ändert sich bei der Menge der möglichen  n ,  wenn die Bedingung "kreuzungsfrei" aufgehoben wird?  Was ändert sich bei der Menge der möglichen  n ,  wenn die Bedingung "gleich lange Wege" aufgehoben wird?

Lösung

Nur  n ≥ 4  kommen in Frage.

Zu jedem Haus gehören  3  Wege. Da jeder Weg zu  2  Häusern gehört, gilt

Anzahl Wege = (3/2) × Anzahl Häuser = (3/2) × n

⇒  n gerade

Nun wird man sich überlegen, ob es einfache Graphen gibt, die das Dorf abbilden können. Zu jedem Knoten gehören drei Kanten; alle Kanten sind gleich lang und überschneiden sich nicht. Ein wenig Probieren (oder der Tipp in der Aufgabenstellung) führt zur folgenden Idee in Bild 1:

Bild 1

Die gestrichelten Linien deuten an, dass hier  n  gerade ist und beliebig groß werden kann. Ganz kleine  n  werden also erstmal nicht betrachtet. Jetzt taucht eine etwas schwierigere Frage auf: Wie muss der Graph an den Enden aussehen? Die Quadrate dürfen ja nicht einfach abbrechen. Im Tipp wurde deshalb der Graph als "Strickleiter" bezeichnet, die an den Enden "verknotet" werden muss. Bild 2 zeigt dafür eine Lösung:


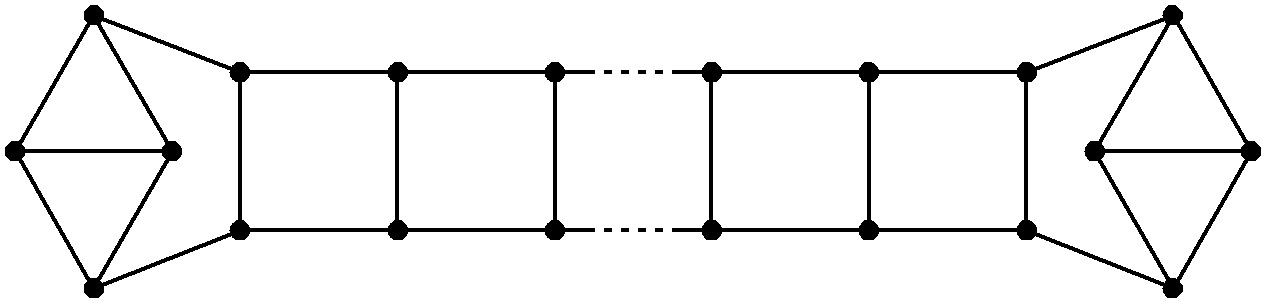
Bild 2

Also gibt es für jedes große gerade  n  ein Dorf, das den Bedingungen genügt. Wenn man in Bild 2 den Graphen maximal zusammenschiebt, kommt man bei  n = 10  aus; also sind alle geraden  n ≥ 10  abgedeckt.

Es bleiben die Fälle  n = 4, 6, 8  zu untersuchen. Das geht nur mit Probieren; die größte Hilfe dabei ist die gleiche Länge aller Kanten, weil dadurch viele Konstellationen wegfallen. Bei  n = 4  und  n = 6  wird man keinen passenden Graph finden; es muss natürlich noch bewiesen werden, dass es keinen gibt (siehe weiter unten). Aber für  n = 8  gibt es eine Lösung. Diese wird nahegelegt durch Bild 2; man muss nur die beiden Rauten an den Enden miteinander verbinden, siehe Bild 3:



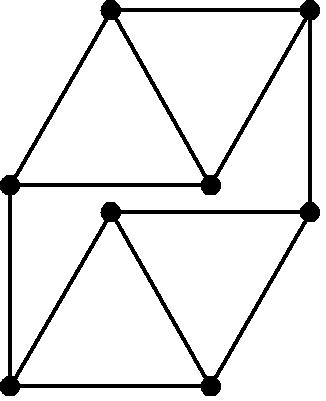
Bild 3

In dem folgenden Kasten sieht man eine Übersicht der bisherigen Ergebnisse:

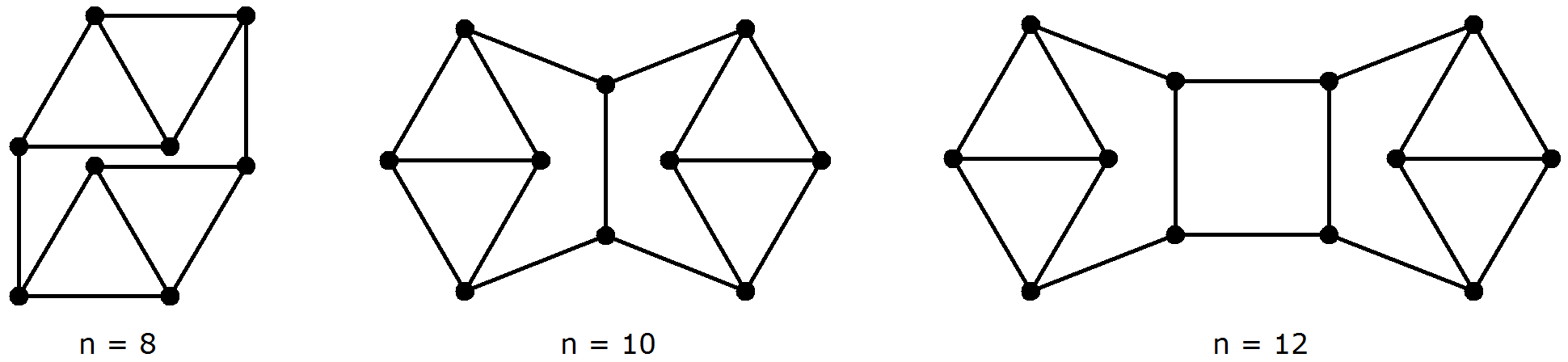
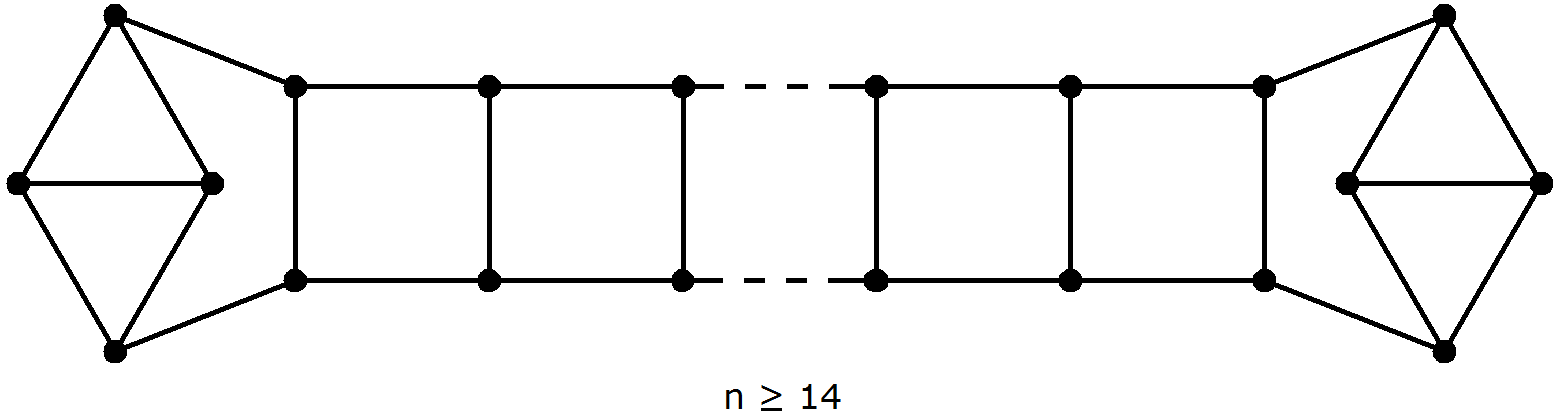
Bild 4

Wir beginnen mit einer beliebigen Kante im Graph des Dorfes; die Endpunkte seien  A  und  B ,  siehe Bild 5. Dann haben  A  und  B  je zwei "freie" Kanten (grün), deren Lage in der linken Skizze noch nicht festliegt. Da es nur noch zwei fehlende Knoten  C  und  D  gibt, müssen sich je eine grüne Kante von  A  und eine grüne Kante von  B  treffen; da alle Kanten die gleiche Länge haben, geht das nur mit zwei gleichseitigen Dreiecken wie in der mittleren Skizze.  C  und  D  haben dort noch eine Kante zu wenig, also müssen sie verbunden werden (rechte Skizze). Diese neue (orangene) Kante ist aber nicht kreuzungsfrei und überdies zu lang. Es gibt somit kein Dorf mit  n = 4 ,  das die Anforderungen erfüllt.

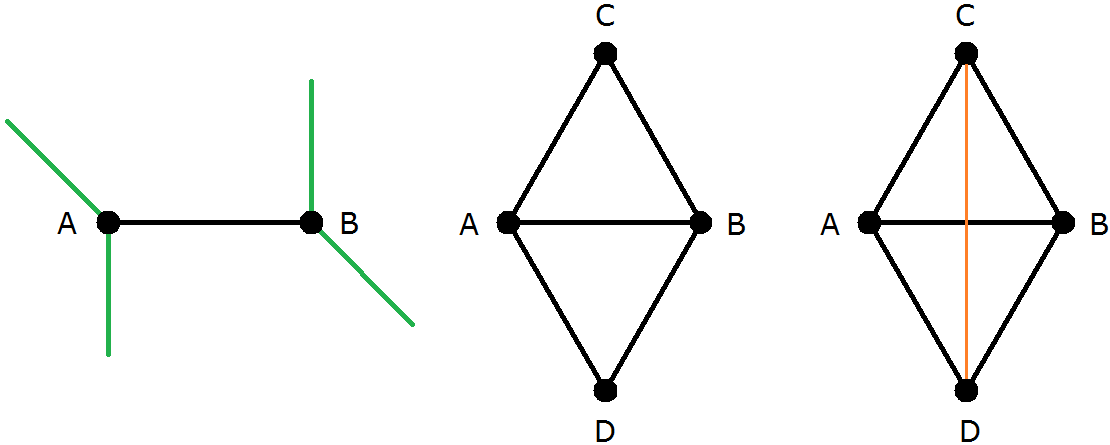
Bild 5


n = 6

Wir beginnen in den folgenden Graphiken zu  n = 6  mit der gleichen Ausgangslage für die Knoten  A, B  wie in Bild 5 links. Für die Lage der grünen Kanten in der linken Skizze sind drei Fälle zu unterscheiden.

Im Folgenden sind Kanten in grün gezeichnet, deren endgültige Lage noch nicht feststeht. Kanten, die keine Änderung mehr erlauben, sind schwarz.

n = 6   1. Fall   Die freien grünen Kanten stoßen paarweise in den Knoten  C, D  zusammen, so wie bei  n = 4 .

Wie in der rechten Skizze von Bild 6a gezeigt, laufen die fehlenden Kanten bei  C  und  D  wegen der gleichen Weglängen zu verschiedenen Knoten; dies sind die noch fehlenden Knoten  E  und  F .  Damit ist die Unmöglichkeit der Konstruktion bereits gezeigt, da  E  und  F  beide jeweils zwei weitere Kanten benötigen würden.

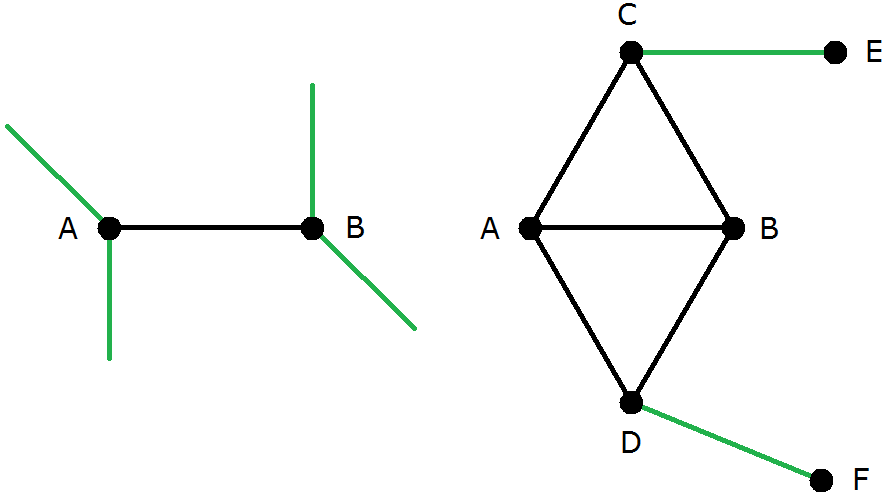
Bild 6a

n = 6   2. Fall   Keine der freien grünen Kanten stößt an eine andere.

Das führt auf die rechte Skizze in Bild 6b. Dort fehlen zwei Kanten bei  C ;  diese können nur nach  D  und  E  führen, was wegen der gleichen Weglängen nicht möglich ist.

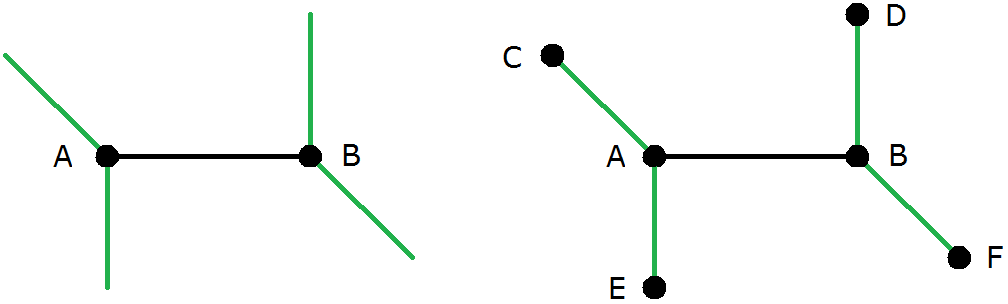
Bild 6b

n = 6   3. Fall   Zwei der freien grünen Kanten laufen zum selben Knoten, die beiden anderen nicht.

Dies sieht man in der mittleren Skizze von Bild 6c. Dort fehlt noch der Knoten  F .  Bei  E  fehlen noch zwei Kanten; diese müssen zu  C  und  F  laufen. In der rechten Skizze sieht man, wie  E  mit  C  durch eine Kante verbunden werden muss; es entstehen zwei gleichseitige Dreiecke. Auch bei  D  fehlen noch zwei Kanten, die mit  E  und  F  verbunden werden müssen. Dies ist wegen der gleichen Weglängen und der Kreuzungsfreiheit nicht möglich.

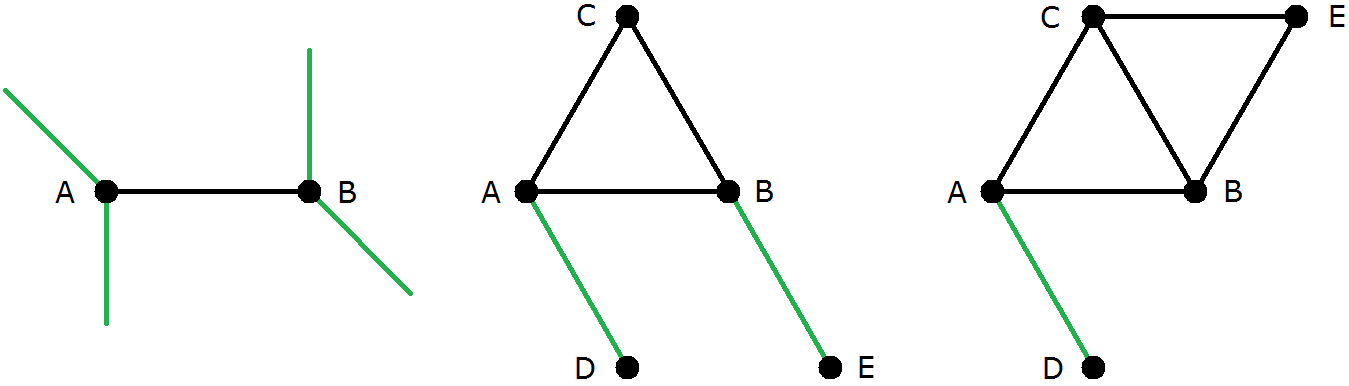
Bild 6c


Damit haben wir die Lösung für unser Hauptproblem:
In dem Dorf, das in der Aufgabenstellung beschrieben ist, muss  n  gerade mit  n ≥ 8  sein.

Der Kasten mit Bild 4 ist ein Beweis ohne Worte für  n ≥ 8 .

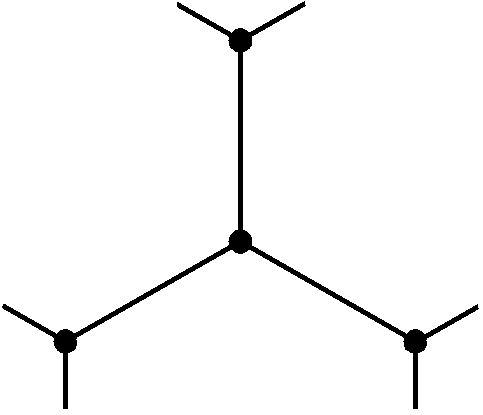
Die Skizzen in Bild 4 sind nicht die einzigen Lösungen. Für einzelne  n  lassen sich andere Dörfer skizzieren, z.B. Bild 7a für  n = 22 ;  diese Skizze ist eine Erweiterung des Bildes in der Aufgabenstellung oben rechts.

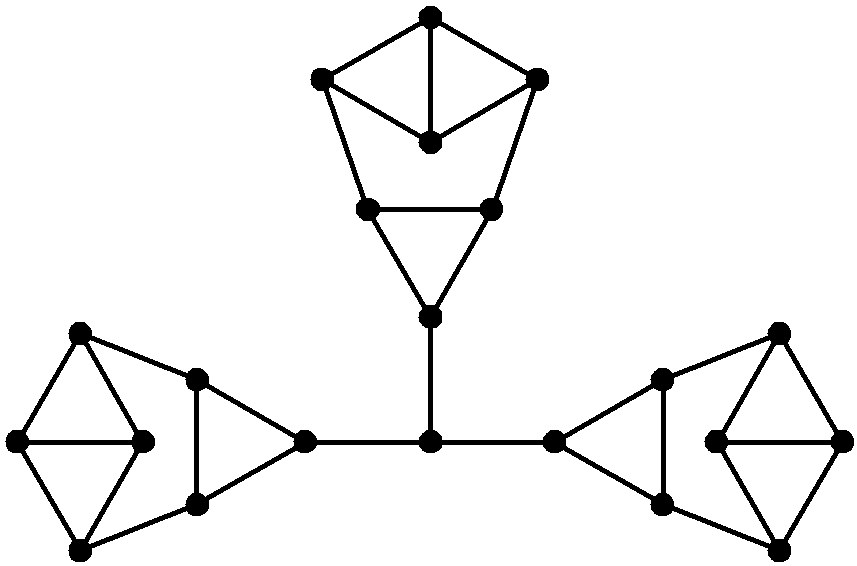
Bild 7a   n = 22

Es gibt aber auch Graphen, die Dörfer unter den vorgegebenen Bedingungen darstellen, die sich für große  n  beliebig erweitern lassen und die anders als in Bild 4 aussehen; in Bild 7b sieht man einige Beispiele, wobei jeweils nur der "innere Kern" der Graphen skizziert ist:

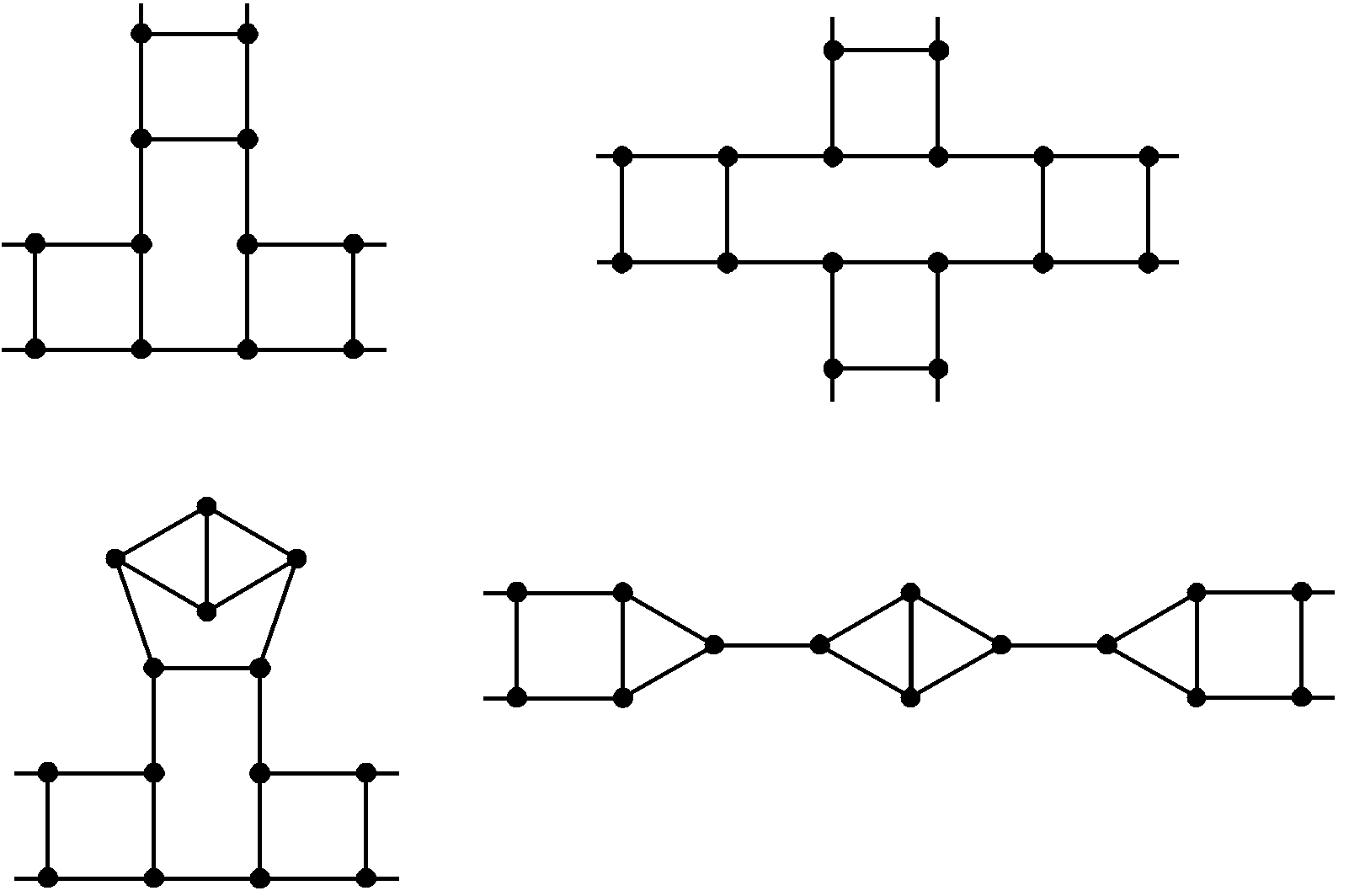
Bild 7b

Es wurde bis hierhin stillschweigend unterstellt, dass die Graphen zusammenhängend sind. Falls das Dorf aus "Inseln" bestehen darf, die untereinander nicht durch Wege verbunden sind, gibt es natürlich viele andere Lösungen; z.B. könnte man für  n = 20  ein "Unterdorf" mit  n₁ = 8  und ein "Oberdorf" mit  n₂ = 12  skizzieren. Für unsere Lösung  " n  gerade  und  n ≥ 8 "  spielt es aber keine Rolle, ob der Graph zusammenhängend ist.

Den Graphen in den Bildern 4, 7a, 7b ist gemeinsam, dass sie im Wesentlichen aus Quadraten und Rauten aufgebaut sind. Gibt es auch ganz andere Lösungen? Der Autor wäre für die Zusendung kreativer "Dorf-Graphen" dankbar (→ E-Mail).

Was ändert sich an der Lösung, wenn die Bedingung "kreuzungsfrei" aufgehoben wird?

Aus Bild 5 wird klar, dass dann für  n = 4  weiterhin keine Lösung existiert, denn die orangene Kante ist zu lang.

Durch ein wenig Probieren, ausgehend von Bild 6b, findet man leicht ein passendes Beispiel für  n = 6 ,  siehe Bild 8.

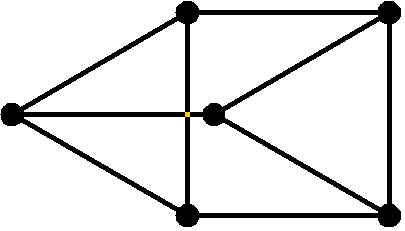
Bild 8

Was ändert sich an der Lösung, wenn die Bedingung "gleich lange Wege" aufgehoben wird?

Für diesen Fall zeigt Bild 9 Graphen für  n = 4  und  n = 6 . Der Graph für  n = 6  wird nahegelegt durch Bild 6b.

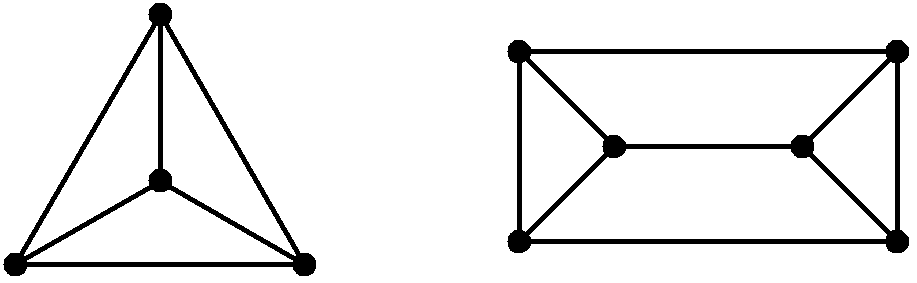
Bild 9

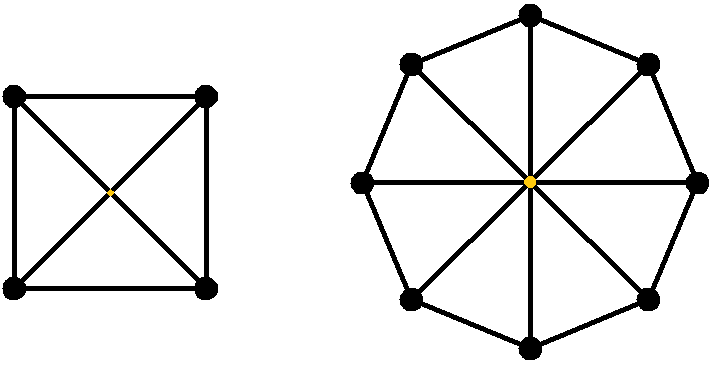
Bild 10


Kategorie: Beweise ohne Worte

Publiziert 2025-12-16          Stand 2024-11-27

voriges Problem   |   Liste aller Probleme mit Lösungen