Manfred Börgens
Mathematische Probleme  # 132		 Liste aller Probleme mit Lösungen
voriges Problem      nächstes Problem		 zur Leitseite


Nur alle 18,6 Jahre sehen wir eine Große Mondwende  —  jetzt ist es wieder soweit.

          Die Lösung steht im unteren Teil der Seite.

     Mit Ergänzungen und Änderungen vom 16.1.2026.

Die Bahnen von Sonne und Mond über unseren Himmel sind in mancher Hinsicht ähnlich, aber es gibt auch mehrere Unterschiede. Die Mondbahn ist deutlich komplizierter, hat aber deswegen auch interessantere Besonderheiten, die sich gut beobachten lassen und die schon in frühgeschichtlichen Zeiten von unseren Vorfahren aufmerksam verfolgt wurden.

In den gemäßigten und den tropischen Breiten der Erde beobachten wir, dass Sonne und Mond in (grob) östlicher Richtung aufgehen, bis zur oberen Kulmination (Höchststand) aufsteigen und in westlicher Richtung untergehen. In den Polarregionen gibt es phasenweise das Phänomen, dass die Sonne bzw. der Mond bei der oberen Kulmination unter dem Horizont oder bei der unteren Kulmination (Tiefststand) über dem Horizont stehen (bei der Sonne bedeutet das, dass sie ganztägig unsichtbar oder ganztägig sichtbar ist). Die Kulminationen beider Himmelskörper unterliegen einer (mehr oder weniger) regelmäßigen Schwankung, was ihre Höhe über oder unter dem Horizont betrifft. Hier treffen wir auf den ersten Unterschied. Die Schwankung in der Kulminationshöhe der Sonne hat einen Jahresrhythmus; zu Sommeranfang steht die Sonne am höchsten und zu Winteranfang am tiefsten. Die Kulminationshöhe des Mondes dagegen schwankt in einem (ungefähr) monatlichen Rhythmus.

Das Thema dieser Seite "Große Mondwende" hat mit einem zweiten Unterschied zwischen Sonne und Mond zu tun. Die Mondbahn verläuft nämlich nicht konstant im selben Winkel zum Äquator, sondern dieser Winkel hat ebenfalls eine periodische Schwankung. Dies führt dazu, dass die höchste und die niedrigste obere Kulmination innerhalb eines Mondumlaufs um die Erde mal mehr und mal weniger weit auseinander liegen (wogegen diese Differenz bei der Sonne weitgehend gleichmäßig bei etwa \(~46,9°\) innerhalb eines Jahres liegt).

Diese Problemseite wird sich vorwiegend damit beschäftigen, wann und von welchen Punkten der Erde der Mond zu sehen ist. Dabei kommt ein dritter Unterschied zur Sonne ins Spiel. Da die Sonne groß und weit entfernt ist, beleuchtet sie immer fast genau eine Hälfte der Erde. Der Mond dagegen ist klein und nahe und beleuchtet nennenswert weniger als eine Hälfte der Erde.

Im Folgenden werden geomathematische Grundkenntnisse nicht vorausgesetzt, da alles Wesentliche, das für die Bearbeitung der Aufgaben erforderlich ist, erläutert wird. Dennoch erleichtert es das Verständnis, wenn man mit den Grundbegriffen bereits vertraut ist. Die Literaturverweise (Links) am Ende der Seite können dabei helfen.


Die Mondbahn aus Sicht eines irdischen Beobachters :  Die wichtigsten Zahlen

Der Mond umläuft die Erde auf einer elliptischen Bahn, hat also keinen konstanten Abstand zur Erde. Da die Schwankung im Abstand keinen bedeutsamen Einfluss auf unsere Problemstellung haben wird, rechnen wir mit dem mittleren Abstand \(_~a_~\) zwischen den Mittelpunkten der Körper:

\(a \approx 385.000~\text{km}\)

Der Radius der Erde \(~r~\) wird hier ohne Berücksichtigung der Polabplattung angegeben:

\(r\approx 6.371~\text{km}\)

Für den Standort des Beobachters benötigen wir nur seine geographische Breite  φ :

φ\(~\in [-90°,~90°]\)

Die Mondbahn ist gegenüber der Äquatorebene abgewinkelt, und zwar im Mittel um ca. \(_~\epsilon_~=_~23,44°\), siehe Bild 1.

Deklination Mond

Bild 1  Erde mit Äquator und Umlaufbahn des Mondes  —  nicht maßstäblich

Zu jedem Zeitpunkt steht der Mond über einem Punkt der Erde senkrecht; dessen geographische Breite ist die Deklination des Mondes \(~\delta~\).  In Bild 2a ist \(~\delta=0°\),  d.h. der Mond (kleiner orangener Punkt) steht über dem Äquator senkrecht. Da der Mond nur den gelben Anteil bescheint, also weniger als die Hälfte der Erde, sieht man den Mond nur in den Breiten  φ\(~\in [_~-90°+\beta,~90°-\beta_~]_~\).  Bild 2b zeigt Deklinationen \(~\delta\gt 0°~\) und \(~\delta\lt 0°\).  —  Für die Ermittlung von \(\delta~\) zu einem gegebenen Zeitpunkt kann man ein astronomisches Jahrbuch heranziehen, das in der Regel einen Wert pro Tag angibt. Dort erkennt man gut, wie sehr sich \(~\delta~\) von einem Tag zum nächsten ändert  –  dies sollte weiter unten bei den Aufgaben beachtet werden.

Deklination Mond = 0

Bild 2a  Nicht maßstäblich
Deklination Mond ungleich 0
Bild 2b  Nicht maßstäblich

Zu den Bildern 1, 2a und 2b ist noch anzumerken, dass während des (annähernd) monatlichen Umlaufs des Mondes sich die Erde täglich um ihre Achse dreht.


Mondwenden

Die Deklination ändert sich periodisch (eine Periode entspricht einem Mondumlauf um die Erde) zwischen \(~-\delta_{max}~\) und \(~\delta_{max}~\)  –  überstreicht also in einem Umlauf einen Winkelbereich von \(~4~\delta_{max}\) .  Wie schon erwähnt, ist \(~\delta_{max}~\) im Mittel gleich \(~23,44°\); dies ist auch der konstante Wert für die maximale Deklination der Sonne. Aber die Mondbahnebene (siehe Bild 1) verändert ihren Winkel zur Äquatorebene der Erde um ca. \(~\pm 5,15°\) in einer Periode von ca. \(18,61\) Jahren. Man beachte, dass \(~\delta_{max}~\) nur in relativ kurzen Zeiträumen (einige Monate) einigermaßen gleich bleibt, da sich \(~\delta_{max}~\) pro Jahr im Durchschnitt um ca. \(~1,1°\) verändert.

\(\delta_{max} \in [~18,3°,~28,6°]\)

Kurz vor der Veröffentlichung dieser Problemseite hat \(~\delta_{max}~\) den größten Wert von ca. \(~28,6°\) erreicht. Dies nennt man eine Große Mondwende. Beim kleinsten Wert \(~\delta_{max} =18,3°\) findet eine Kleine Mondwende statt, das nächste Mal im Jahr 2034.

Die aktuelle Große Mondwende hat u.a. zur Folge, dass es einen extrem niedrig stehenden Vollmond geben wird. Der exakte Zeitpunkt dieses Vollmonds ist \(~10.{_~}_~\text{Juli}{_~}_~2025_~,{_~}_~20:37~\text{UTC}\). Die Monddeklination beträgt zu dieser Zeit \(-28°\).  Auf der östlichen geographischen Länge \(~50°45'_~\) ist dann Mitternacht und der Vollmond steht im Zenit. Auf diesem Meridian erreicht er z.B. auf dem \(~50.\) Breitengrad eine Höhe von lediglich \(12°_~\) (in Deutschland gilt das nur näherungsweise, da streng genommen um Mitternacht (Ortszeit, Sommerzeit und Zeitgleichung beachten!) der Vollmondzeitpunkt schon verstrichen ist, aber der Unterschied ist nur sehr gering). Diese Vollmondhöhe ist minimal, bezogen auf die letzten \(~18,61~\) und die nächsten \(~18,61~\) Jahre.

Die genannten Bahndaten erlauben  –  falls keine hohe Genauigkeit verlangt wird  –  eine Modellierung von \(~\delta~\) durch zwei Cosinus-Schwingungen: \[\delta \approx \left(23,44°+5,15°\cdot\text{cos}~\frac{2 \pi\cdot x}{6798,4}\right) \cdot \text{cos}~\frac{2 \pi \cdot x}{27,3217}\] Der rechte Cosinus-Term beschreibt den periodischen Verlauf der Deklination mit einem siderischen Monat als Periodenlänge. Der Klammerausdruck steht für die Amplitude \(~\delta_{max~}\), die ihrerseits periodisch um den Wert \(_~23,44°\) schwingt, mit einer Periodenlänge von ca. \(18,61_~\) Jahren. \(~x~\) ist eine Datumsangabe in Tagen, wobei \(_~x=0_~\) für einen Zeitpunkt steht, an dem \(~\delta~\) den größtmöglichen Wert (ca. \(28,6°\)) annimmt. Diese Modellierung gibt ein brauchbares Bild von der Änderung von \(~\delta~\) im zeitlichen Verlauf (siehe Bild 2c für einen Ausschnitt aus einer Periode), berücksichtigt aber nicht die zahlreichen kleinen Bahnstörungen des Mondes (auch die vier Zahlenwerte in der Formel sind nicht konstant, sondern unterliegen kleinen periodischen Schwankungen oder langfristigen Trends).

Graph Deklination Mond

Bild 2c  Deklination des Mondes - waagerechte Achse: Tage, senkrechte Achse: \(_~\delta\)

Wenn man den Mondlauf nicht ganz genau beobachtet, könnte man vermuten, dass in der Mitte zwischen Kleiner und Großer Mondwende (oder umgekehrt) die Mondbahn genau in der Ekliptik liegt. Das ist nicht so. Die Mondwenden kommen zustande, weil die Mondbahn immer um \(_~5,15°\) gegenüber der Ekliptik geneigt ist; die "Achse" dieser Neigung ist ein Durchmesser der Mondbahn, der sich in \(_~18,61_~\) Jahren einmal vollständig dreht. Dies wird in Bild 2d graphisch dargestellt. Die Graphiken sind stark schematisiert und zielen nur darauf ab, die beobachtbaren Phänomene des Mondlaufs zu erläutern.

Bild 2d zeigt in der ersten Graphik den Blick von Norden auf die Ekliptikebene. Die Erdachse ist um \(_~\epsilon_~=_~23,44°\) gegenüber dieser Ebene geneigt; dies erkennt man daran, dass der Nordpol  N  aus dem Zentrum herausgerückt wurde und dass man einen Teil der Südhalbkugel erkennen kann; \(_~0°\) steht für den Äquator. Hier und in den beiden folgenden Graphiken liegt der Breitengrad  φ  des Beobachters in den gemäßigten Breiten der Nordhalbkugel, also zwischen dem nördlichen Wendekreis und dem nördlichen Polarkreis.  –  Was bedeutet "tief stehen" und "hoch stehen" bei Winter- bzw. Sommeranfang? Die Sonne steht genau im Süden bei \(_~90°-_~\) φ \(_~\mp_~\epsilon_~\). Für den Mond gilt das nur im Mittel; das wird aus den beiden anderen Graphiken deutlich.

Die zweite Graphik enthält zusätzlich die Mondbahn bei einer Mondwende (da der Mondwenden-Zyklus \(_~18,61_~\) Jahre dauert, kommt es hier nicht auf den genauen Zeitpunkt an). Die oben erwähnte "Achse" ist in blau eingezeichnet. Bei einer Großen Mondwende liegt die Mondbahn in dunkelgrün unterhalb der Ekliptik und in hellgrün oberhalb; bei einer Kleinen Mondwende ist es umgekehrt. Die Graphik gibt vier Mondhöhen im Süden über dem Horizont des Beobachters an. Dabei wird nur der Idealfall abgebildet, dass der Mond zu Beginn einer Jahreszeit genau an der eingezeichneten Stelle steht; das ist natürlich nur selten der Fall, deshalb handelt es sich bei den vier Mondhöhen nur um ungefähre Werte. Sieht man beispielsweise ungefähr zu Herbstanfang einen ungefähr zunehmenden Halbmond (d.h. der Mond steht in der Graphik ungefähr am oberen Rand), so ist seine Kulminationshöhe ungefähr \(_~61,4°-_~\) φ  bei einer Großen und \(_~71,7°-_~\) φ  bei einer Kleinen Mondwende.

In der dritten Graphik wird deutlich, warum die Mondbahn zu keinem Zeitpunkt in der Ekliptik liegt. Die Bahn ist zu einem mittleren Zeitpunkt zwischen den Mondwenden dargestellt; ihre Neigung von \(_~5,15°\) gegenüber der Ekliptik (und damit die blaue Achse) ist gegenüber der mittleren Graphik um \(_~90°\) gedreht. Es sind wieder vier Kulminationshöhen eingetragen, die zeigen, dass sich die Achse im Uhrzeigersinn dreht. Insbesondere gibt es einen vielleicht nicht sehr bekannten, aber interessanten und beobachtbaren Effekt der \(_~5,15°-\)Neigung: Wenn z.B. (ungefähr) mittig zwischen den Mondwenden zu Sommer- oder Winteranfang der Vollmond am Himmel steht (also in der Graphik ganz oben oder ganz unten), dann stehen der vorhergehende zunehmende und der folgende abnehmende Halbmond nicht etwa in gleicher Kulminationshöhe, sondern diese Höhen unterscheiden sich um \(_~10,3°\) (siehe Angaben neben der linken und der rechten Mondscheibe).

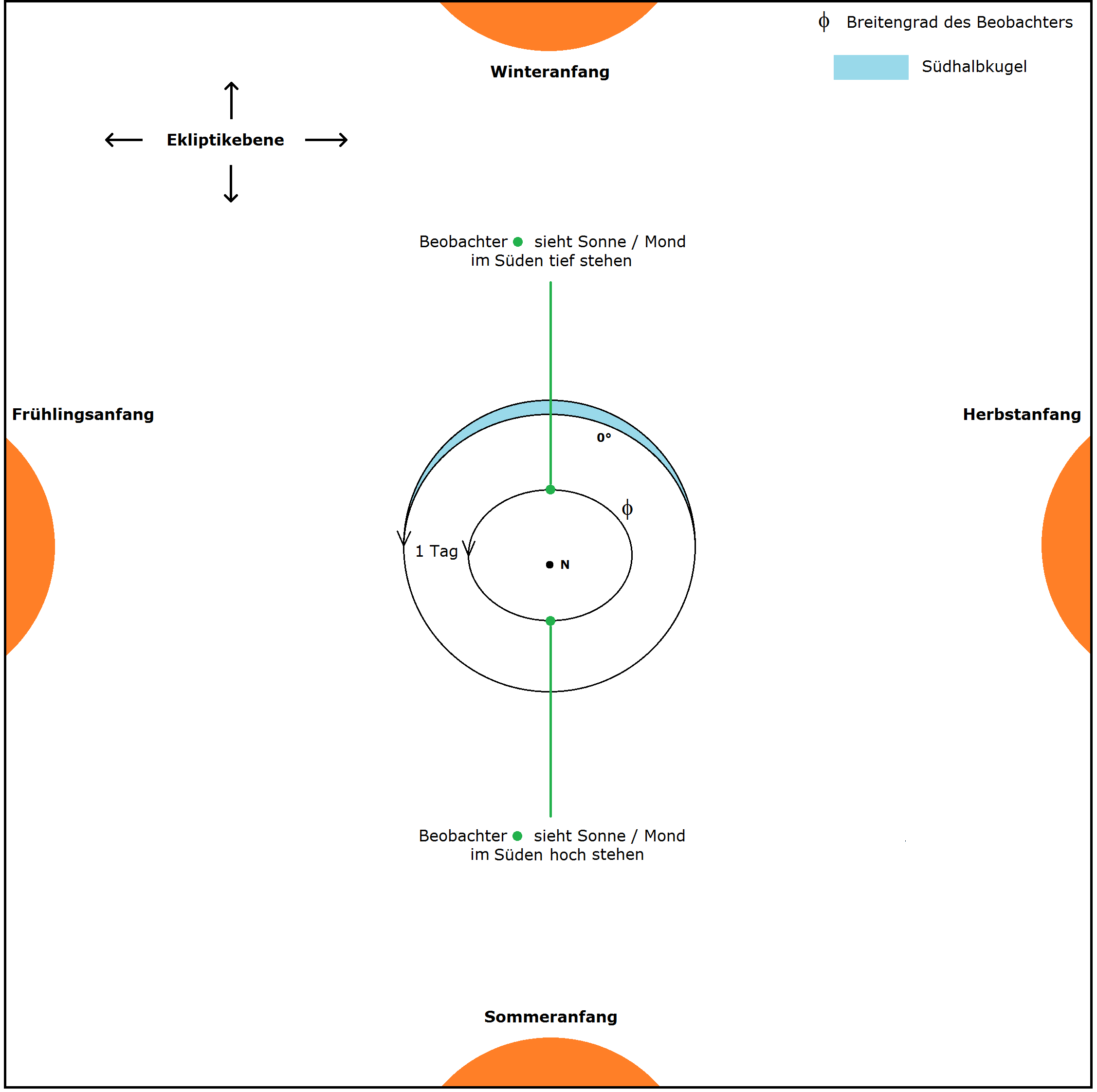
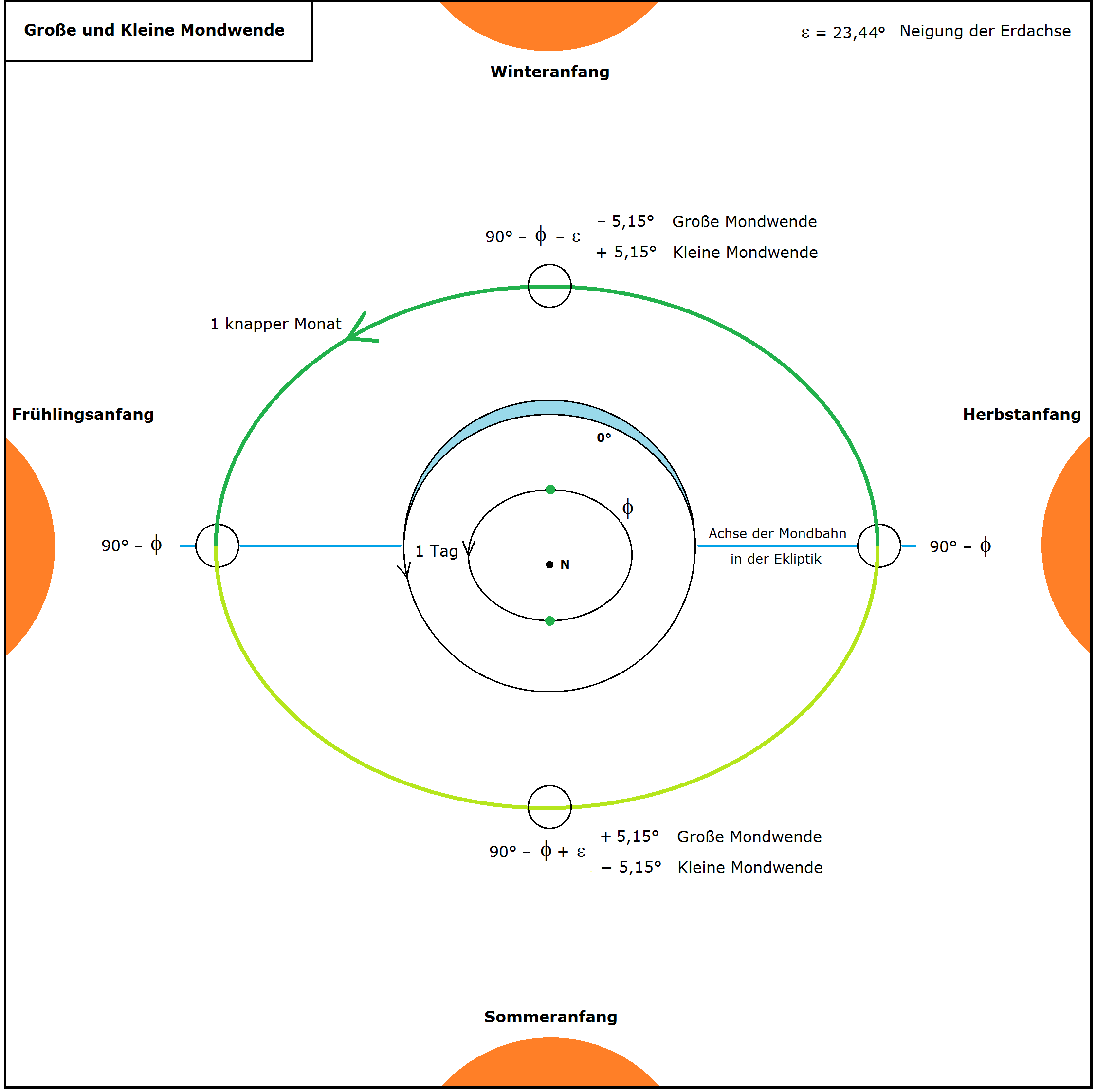
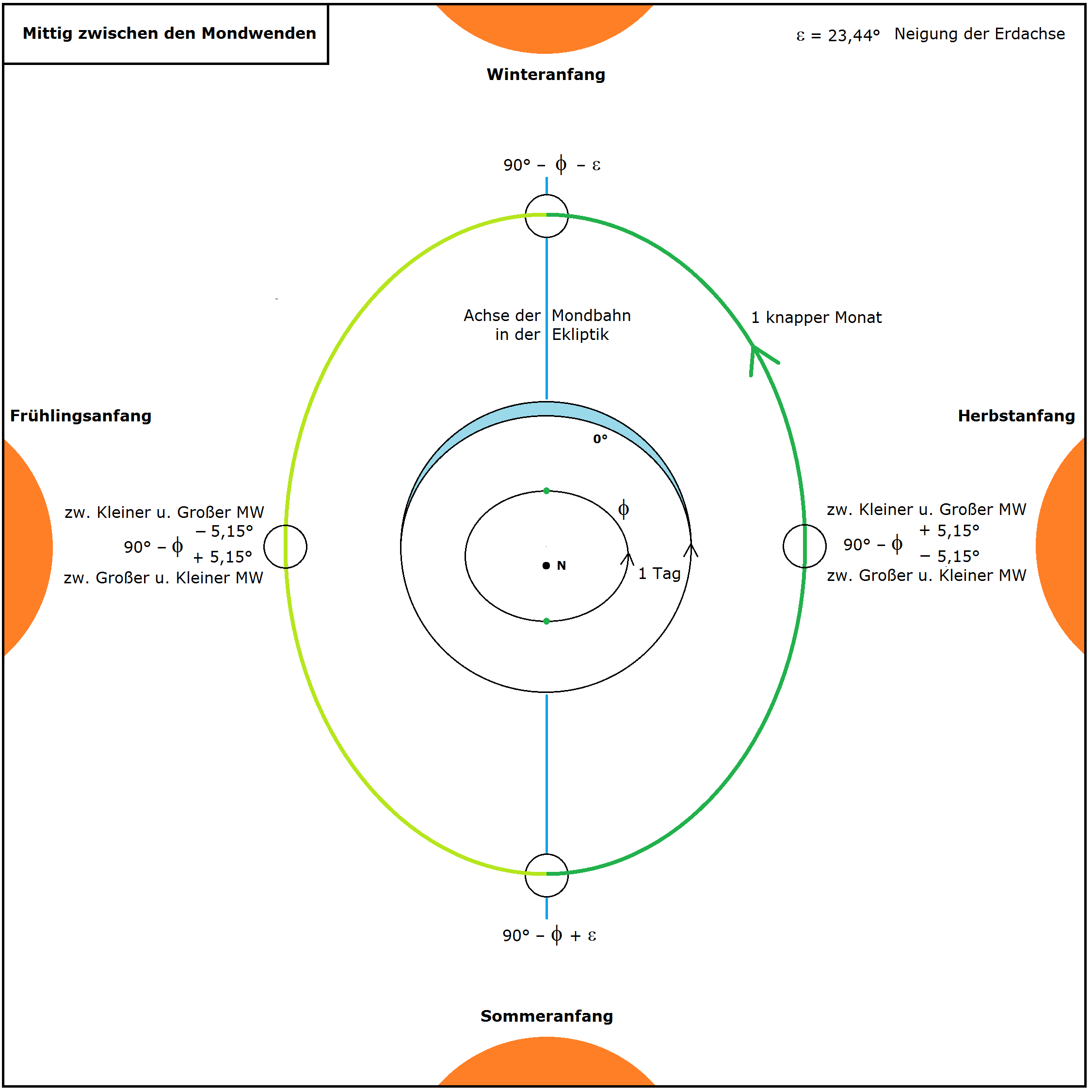
ohne Mondbahn Grosse und Kleine MW zwischen den MW

Bild 2d  Nicht maßstäblich. Erläuterungen im Text über dem Bild.

Es folgen mehrere Beispiele, die die zweite und die dritte Graphik in Bild 2d betreffen. Die Tabellenwerte sind dem  Kosmos Himmelsjahr  entnommen.


Bemerkungen

1.  Der Monat hat seine etymologische Wurzel zwar im Mond, aber der Umlauf des Mondes um die Erde passt nicht exakt zum heutigen kalendarischen Monat. Die Zeit zwischen zwei Vollmonden beträgt ca. \(~29,5\) Tage (synodischer Monat) und die Zeit zwischen zwei maximalen oberen Kulminationen, d.h. mit einer Deklination von \(~\delta_{max}~\),  beträgt ca. \(~27,3\) Tage (siderischer Monat). Der Unterschied erklärt sich daraus, dass sich nach einem Vollmond und einem anschließenden vollständigen Mondumlauf die Erde ein Stück auf ihrer Bahn um die Sonne weiterbewegt hat, und der Mond noch nicht wieder in einer Linie mit Erde und Sonne steht und deshalb noch nicht ganz voll ist.  —  Wenn man jeden Tag die obere Kulmination des Mondes misst, erkennt man gut die Abfolge der siderischen Monate; dies war schon in frühgeschichtlichen Kulturen bekannt.

2.  Es gibt eine ganze Reihe interessanter Fragestellungen, die den Mond betreffen, die aber hier nicht behandelt werden. Unterschiede zum Sonnenlauf gibt es nämlich noch mehr als bisher erwähnt wurden: Auf- und Untergänge des Monds können zu jeder Zeit des Tages und der Nacht stattfinden, außerdem zeigt der Mond Phasen  —  diese Phänomene kommen auf dieser Problemseite nicht vor.

3.  Die Zahlenangaben im vorigen Abschnitt sind nur gerundet, aber vor allem unterliegen sie langfristigen Schwankungen. Falls man das ganz genau wissen möchte, kann man die Literaturverweise am Ende dieser Seite zu Rate ziehen.

4.  Die folgenden Aufgaben sollen für ein mathematisches Erde-Mond-Modell gelöst werden, das von vereinfachenden Annahmen ausgeht. Die Polabplattung der Erde und die Refraktion durch die Atmosphäre werden nicht berücksichtigt, und die Sichtbarkeit des Mondes wird auf seinen Mittelpunkt reduziert. Dadurch ergibt sich eine leichte Verzerrung der Ergebnisse gegenüber den tatsächlich zu beobachtenden Phänomenen.  —  Bei den Lösungen der Aufgaben ist auch zu beachten, dass sich die Monddeklination viel schneller verändert als die der Sonne: Das gesamte Intervall \(~[-\delta_{max},~\delta_{max}]~\) wird von \(~\delta~\) in knapp zwei Wochen durchlaufen.


Aufgabe 1

Wie groß ist der Winkel \(_~\beta_~\) in Bild 2a ?
Welcher prozentuale Anteil der Erde wird vom Mond beleuchtet ?  Zur Erinnerung: Relevant ist hier immer nur der Mittelpunkt der Mondscheibe.


Aufgabe 2

Eine Änderung der Deklination \(~\delta~\) bewirkt, dass die Berührpunkte der Kreistangenten in den Bildern 2a und 2b die gleiche Winkeländerung erfahren. Warum ist das so ?

D.h. Deklination \(~\delta~\) und Sichtbarkeitsgrenze  φ  laufen "parallel". Aber Vorsicht:  φ  kann dabei \(~\pm 90°~\) überschreiten und ist dann durch \(~\pm 180°-\) φ  zu ersetzen.


Aufgabe 3

Auf welchen Breitengraden liegen die Tangenten-Berührpunkte in den Bildern 2a und 2b ?  Was folgt daraus für die Extremalwerte \(~\delta = \pm~\delta_{max}~\)?


Aufgabe 4

Für feste Deklination \(~\delta ~\):  Auf welchen Breitengraden  φ
    –  geht der Mond auf und unter ?
    –  bleibt der Mond bei der oberen Kulmination unter dem Horizont (geht also nicht auf) ?
    –  steht der Mond bei seiner unteren Kulmination über dem Horizont (geht also nicht unter) ?

Wie erscheint der Mond den Beobachtern an den Grenzen dieser drei Zonen ?

Führen Sie eine Beispielrechnung für \(~\delta=0° ~\) und \(~\delta=\delta_{max}=28,6° ~\)(Mitte 2025) durch.


Aufgabe 5

Für feste Breite  φ  wird ein vollständiger Mondumlauf betrachtet, also ein siderischer Monat:  Bei welchen Deklinationen \(~\delta~\)
    –  geht der Mond auf und unter ?
    –  bleibt der Mond bei der oberen Kulmination unter dem Horizont ?
    –  steht der Mond bei seiner unteren Kulmination über dem Horizont ?

Wie erscheint der Mond den Beobachtern an den Grenzen dieser drei Zonen ?

Führen Sie eine Beispielrechnung für \(~\delta_{max}=28,6° ~\)(Mitte 2025) und  φ \(=50° ~\) bzw.  φ \(=62,3° ~\) bzw.  φ \(=70° ~\) durch.


Aufgabe 6

Warum gibt es für das Mondlicht keinen eindeutigen Polarkreis auf der Erde, sondern nur einen "Polarstreifen", der dazu noch "wandert"?


Aufgabe 7

Nun könnte es einen interessanten Vergleich zu anderen Monden (siehe kleine Liste am Ende der Aufgabe) in unserem Sonnensystem geben. Es stellt sich aber heraus, dass das ziemlich langweilig ist.

Der Grund dafür ist, dass unser Mond sich ganz anders verhält als die Monde unserer Nachbarplaneten. Denn diese laufen fast exakt in der Äquatorebene um ihren Planeten und nicht in der Ekliptik, d.h. es gilt immer \(_~\delta\approx 0°\). Unser Mond verhält sich in dieser Hinsicht also eher wie ein Planet und hat in der Gesellschaft der Monde eine ausgeprägte Sonderstellung.

Beobachter auf anderen Planeten sehen ihre Monde regelmäßig auf- und untergehen, und die oberen Deklinationen finden immer auf \(~90°\) – φ  statt, von sehr kleinen Abweichungen abgesehen. Die Fragestellungen in den Aufgaben 3 bis 6 bieten sich also für die fremden Monde nicht an. Andererseits gibt es unaufhörlich Sonnen- oder Mondfinsternisse, viel mehr als auf der Erde.

Bemerkenswert ist das Phänomen, dass auf den Polen der Nachbarplaneten die Monde nie beobachtet werden können. Wie weit die Region um einen Pol reicht, in der man einen bestimmten Mond nicht (also nie) sehen kann, lässt sich mit dem Winkel \(_~\beta_~\) aus Aufgabe 1 berechnen, da man näherungsweise \(_~\delta=0°\) setzen kann. Man muss dazu lediglich den Radius des Mutterplaneten und den Abstand der Mittelpunkte von Planet und Mond nachschlagen.

In welchen Regionen des Planeten ist der jeweilige Mond (siehe folgende Liste) unsichtbar? Berechnen Sie dazu \(_~\beta_~\) und den %-Wert für die Kugelkappe wie in Aufgabe 1:

Marsmonde Phobos und Deimos
Die vier Galileischen Jupitermonde
Saturnmond Titan

Lösung


Aufgabe 1

o   Wie groß ist der Winkel \(_~\beta_~\) in Bild 2a ?
o   Welcher prozentuale Anteil der Erde wird vom Mond beleuchtet ?

Die eingezeichneten Radien zu den Berührpunkten stehen im rechten Winkel zu den Tangenten. Somit gilt \[\text{cos}~(_~90°-\beta_~)=\frac{r}{a}~~~~~\Rightarrow~~~~~\beta~\approx~0,95°\] Die Mantelfläche einer Kugelkappe berechnet man mit \(~M_{Kappe}=2~\pi~r^2~\left(1-\text{cos}~(_~90°-\beta_~)\right)~\) und die Oberfläche der Kugel mit \(~O_{Kugel}=4~\pi~r^2~\).  Damit erhält man den gesuchten Anteil: \[\frac{M_{Kappe}}{O_{Kugel}} \cdot 100\%~=~\frac{a-r}{2 \cdot a}\cdot 100\%~\approx~49,17\%\] In Blog # 42 wird eine andere Berechnungsmethode angegeben, mit dem Brotkrustentheorem des Archimedes.


Aufgabe 2

o   Eine Änderung der Deklination \(~\delta~\) bewirkt, dass die Berührpunkte der Kreistangenten in den Bildern 2a und 2b die gleiche Winkeländerung erfahren. Warum ist das so ?

Deklination Mond

Bild 3  Nicht maßstäblich

In Bild 3 sehen wir eine Winkeländerung um \(~\delta_2~\) (dass wir dort von \(~\delta_1=0°~\) ausgehen und \(~\delta_2~>0°~\) wählen, beeinträchtigt die Allgemeingültigkeit der Argumentation nicht, da sich ganze Bild drehen lässt). Die langen grünen und schwarzen Linien sind die Verbindungsstrecken vom Mond zum Erdmittelpunkt und zu den oberen Berührpunkten. Die Winkeländerung des Mondes \(~\delta_2~\),  die durch die untere grüne Linie gegenüber der unteren schwarzen Linie erzeugt wird (farbig markiert), überträgt sich auf die Breite des Erdglobus (Berührpunkte der grünen Tangente und der schwarzen Tangente), da das grüne und das schwarze Dreieck rechtwinklig und daher ähnlich sind.


Aufgabe 3

o   Auf welchen Breitengraden liegen die Tangenten-Berührpunkte in den Bildern 2a und 2b ?
o   Was folgt daraus für die Extremalwerte \(~\delta = \pm~\delta_{max}~\)?

Der obere Tangenten-Berührpunkt soll die Breite  φ\(_1{_~}\) haben, der untere die Breite  φ\(_2{_~}\). Mit den Bildern 2a,b und Aufgabe 2 erhält man:


\(|\delta| \le \beta~~~~~~\rightarrow~~~~~\)φ\(_1=90°-\beta+\delta~~~~~~~~\)φ\(_2=-90°+\beta+\delta\)

\(~~~~~~\rightarrow~~~~~\)φ\(_{1,2}=\pm (90°-\beta)+\delta\)

\(\delta \gt \beta ~~~~~~~~\rightarrow~~~~~\)φ\(_1=90°+\beta-\delta~~~~~~~~\)φ\(_2=-90°+\beta+\delta\)

\(~~~~~~\rightarrow~~~~~\)φ\(_{1,2}=\pm (90°-\delta)+\beta\)

\(\delta \lt -\beta ~~~~~\rightarrow~~~~~\)φ\(_1=90°-\beta+\delta~~~~~~~~\)φ\(_2=-90°-\beta-\delta\)

\(~~~~~~\rightarrow~~~~~\)φ\(_{1,2}=\pm (90°+\delta)-\beta\)

Setzt man die Extremalwerte \(~\delta = \delta_{max}\gt \beta~\) und \(~\delta = -\delta_{max} \lt -\beta~\) ein, so erhält man die Breitengrade in Bild 4.

Polarkreise

Bild 4  Nicht maßstäblich


Aufgabe 4

o   Für feste Deklination \(~\delta ~\):  Auf welchen Breitengraden  φ
    –  geht der Mond auf und unter ?
    –  bleibt der Mond bei der oberen Kulmination unter dem Horizont ("Mond unsichtbar") ?
    –  steht der Mond bei seiner unteren Kulmination über dem Horizont ("Mond dauerhaft sichtbar") ?

o   Wie erscheint der Mond den Beobachtern an den Grenzen dieser drei Zonen ?

o   Führen Sie Beispielrechnungen für \(~\delta=0° ~\) und \(~\delta=\delta_{max}=28,6° ~\)(Frühling 2025) durch.

Aus Aufgabe 3 folgt:
φ \(\in(\) φ\(_2,~\)φ\(_1)~~~~~~\rightarrow~~~~~\)Mond geht auf und unter.
φ \(\ge\) φ\(_1~~~~\wedge~~~~\delta \lt \beta \)
\(~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\rightarrow~~~~~\)Mond ist unsichtbar.
φ \(\le\) φ\(_2~~~~\wedge~~~~\delta \gt -\beta \)
φ \(\ge\) φ\(_1~~~~\wedge~~~~\delta \ge \beta \)
\(~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\rightarrow~~~~~\)Mond ist dauerhaft sichtbar.
φ \(\le\) φ\(_2~~~~\wedge~~~~\delta \le -\beta \)

Was sieht man an den "Grenzen"  φ = φ\(_{1,2}~\)?

"unsichtbar" bedeutet dann, dass die obere Mondhälfte nur für einen minimalen Moment am Horizont erscheint.

"ganztägig sichtbar" bedeutet dann, dass die untere Mondhälfte nur für einen minimalen Moment unter den Horizont sinkt.

Ein Sonderfall ist \(~\delta = \pm~\beta~\) mit  φ \(=\pm~90°\). In diesem Moment sieht man den Mond am Pol auf- oder untergehen.

Beispiele

\(\delta = 0°~~~\Rightarrow~~~\)φ\(_{1,2}=\pm~89,05°\)

      Für  φ \(\in (-89,05°,~89,05°)~\) geht der Mond auf und unter, ansonsten ist er unsichtbar.

\(\delta = 28,6°~~~\Rightarrow~~~\)φ\(_1=62,35°~~,~~~\)φ\(_2=-60,45°\)   Große Mondwende, so wie zum Zeitpunkt der Veröffentlichung dieses Problems

      Für  φ \(\in (-60,45°,~62,35°)~\) geht der Mond auf und unter.

      Für  φ \(\le -60,45°~\) ist der Mond unsichtbar.

      Für  φ \(\ge 62,35°~\) ist der Mond dauerhaft sichtbar.   Zum Zeitpunkt der Veröffentlichung dieses Problems ist also der Mond in Europa nördlich der Breite von Alesund (Norwegen) und Sundsvall (Schweden) sowie in ganz Island ganztägig zu sehen.


Aufgabe 5

o   Für feste Breite  φ  wird ein vollständiger Mondumlauf betrachtet, also ein siderischer Monat:  Bei welchen Deklinationen \(~\delta~\)
    –  geht der Mond auf und unter ?
    –  bleibt der Mond bei der oberen Kulmination unter dem Horizont ?
    –  steht der Mond bei seiner unteren Kulmination über dem Horizont ?

o   Wie erscheint der Mond den Beobachtern an den Grenzen dieser drei Zonen ?

o   Führen Sie eine Beispielrechnung für \(~\delta_{max}=28,6° ~\)(Frühling 2025) und  φ \(=50° ~\) bzw.  φ \(=62,3° ~\) bzw.  φ \(=70° ~\) durch.

Hier können wir uns auf die Nordhalbkugel  ( φ \(\ge 0°~\)) beschränken; für die Südhalbkugel sind die Vorzeichen von  φ  und  δ  zu vertauschen; aus  φ\(_1~\) wird  -φ\(_2~\).  Aus den Aufgaben 3 und 4 und Bild 4 folgt:
\(\delta \lt\beta~~~~~~\)          φ \(\ge\) φ\(_1~~~~~~\rightarrow~~~~~\)Mond ist unsichtbar.
                       φ \(\lt\) φ\(_1~~~~~~\rightarrow~~~~~\)Mond geht auf und unter.
\(\delta \ge \beta~~~~~~\)          φ \(\ge\) φ\(_1~~~~~~\rightarrow~~~~~\)Mond ist dauerhaft sichtbar.
                       φ \(\lt\) φ\(_1~~~~~~\rightarrow~~~~~\)Mond geht auf und unter.

Grenzfall: \(~\delta = \beta~\) mit  φ \(=90°\).  In diesem Moment sieht man den Mond am Pol auf- oder untergehen.

Beispiele
φ \(=50°~~~~\rightarrow~~~~\)Für alle \(~\delta~\) ist  φ < φ\(_1~\) nach Aufgabe 3.\(~~~~\rightarrow~~~~\)Mond geht immer auf und unter, unabhängig von \(~\delta_{max}~\).
φ \(=62,3°~~~~\rightarrow~~~~\)Für \(~\delta \lt \beta~\) ist  φ\(_1=89,05°+\delta~\).
                   φ\(~\ge~\)φ\(_1~~~\Leftrightarrow~~~\delta \le -26,75°\)
\(~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\delta \in [-28,6°,-26,75°]~~~~\rightarrow~~~~\) Mond ist unsichtbar.
\(~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\delta \in (-26,75°,~0,95°)~~~~~\rightarrow~~~~\) Mond geht auf und unter.

                         Für \(~\delta \ge \beta~\) ist  φ\(_1=90,95°-\delta~\) und daher immer  φ\(~\lt~\)φ\(_1~\).
\(~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\delta \in [0,95°,~28,6°]~~~~~~~~~~~~\rightarrow~~~~\) Mond geht auf und unter.

Zusammengefasst gilt: Für \(~\delta \in [-28,6°,-26,75°]_~\) ist der Mond unsichtbar, für größere Deklinationen geht er auf und unter.
φ \(=70°~~~~\rightarrow~~~~\)Für \(~\delta \lt \beta~\) ist  φ\(_1=89,05°+\delta_~\).
                   φ\(~\ge~\)φ\(_1~~~\Leftrightarrow~~~\delta \le -19,05°\)
\(~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\delta \in [-28,6°,-19,05°]~~~~\rightarrow~~~~\) Mond ist unsichtbar.
\(~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\delta \in (-19,05°,~0,95°)~~~~~~\rightarrow~~~~\) Mond geht auf und unter.

                         Für \(~\delta \ge \beta~\) ist  φ\(_1=90,95°-\delta~\).
                   φ\(~\ge~\)φ\(_1~~~\Leftrightarrow~~~\delta \ge 20,95°\)
\(~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\delta \in [0,95°,~20,95°)~~~~~~~~~~~~\rightarrow~~~~\) Mond geht auf und unter.
\(~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\delta \in [20,95°,~28,6°]~~~~~~~~~~~~\rightarrow~~~~\) Mond ist dauerhaft sichtbar.

Zusammengefasst gilt: Für \(~\delta \in (-19,05°,~20,95°)~\) geht der Mond auf und unter, für kleinere Deklinationen ist er unsichtbar, für größere ist er dauerhaft sichtbar.

Aufgabe 6

o   Warum gibt es für das Mondlicht keinen eindeutigen Polarkreis auf der Erde, sondern nur einen "Polarstreifen", der dazu noch "wandert"?

Schauen wir zuerst auf das System Erde - Sonne. In den Polarregionen, also für  |φ|\(\gt 66,55°\), trifft man auf drei Phänomene: Zeitweise geht die Sonne auf und unter, zeitweise ist sie den ganzen Tag über nicht zu sehen, und zeitweise steht sie den ganzen Tag am Himmel. Außerhalb der Polaregionen geht die Sonne jeden Tag auf und unter. Bild 4 zeigt, dass dies für den Mond nicht gelten kann. Die gelbe Fläche bewegt sich in einem siderischen Monat zwischen der linken und der rechten Skizze und wieder zurück. Die Region auf der Nordhalbkugel, in der der Mond immer auf- und untergeht, lässt sich in Bild 4 ablesen:

φ \(\lt~90°-\epsilon -\delta_{max}~~~~\rightarrow~~~~\)Mond geht immer auf und unter.

Wo trifft man beim Mond auf alle drei bei der Sonne erwähnten Phänomene? Dies gilt nach Bild 4 für:

φ \(\gt~90°+\epsilon -\delta_{max}~~~~\rightarrow~~~~\)Mond geht zeitweise auf und unter, ist zeitweise nicht sichtbar, und ist zeitweise dauerhaft sichtbar.

Für den Zwischenbereich zeigt Bild 4:

φ \(\in [~90°-\epsilon -\delta_{max~},~90°+\epsilon -\delta_{max~}]~~~~\rightarrow~~~~\)Für große Deklinationen geht der Mond auf und unter, für kleine Deklinationen bleibt der Mond unter dem Horizont. Dieses Intervall wird in Bild 5 skizziert:

Polarkreise

Bild 5  Polar"streifen" (dunkelgrün) übernehmen für den Mond die Rolle der Polarkreise, hier für die Nordhalbkugel; hellgrün sind die südlichsten und nördlichsten dieser Streifen eingezeichnet  —  nicht maßstäblich

Wann wechseln für einen Beobachter in diesem schmalen Streifen (\(_~2_~\beta=1,9°\) breit) "Mond auf/unter" und "unsichtbar"? Die entsprechenden Berechnungen wurden bereits im zweiten Beispiel von Aufgabe 5 durchgeführt. Nimmt man dort statt \(~62,3°\) ein beliebiges, aber festes  φ ,  so bleibt der Mond unsichtbar für \(~\delta~\in [-\delta_{max~},~\)φ \(-~89,05°]~\).  Dieser Deklinationsbereich hat die Breite \(~0°\) am unteren Rand des Zwischenbereichs (φ-Streifen) und \(~1,9°\) am oberen Rand. Nun ist dieser Streifen sehr schmal, außerdem ändert sich \(~\delta~\) sehr schnell, also ist das Ergebnis vorwiegend von mathematischem Interesse; nur aufmerksame Beobachter werden erkennen, dass sie sich gerade in diesem Streifen aufhalten.

Wichtiger als der Unterschied zwischen "Polarkreis" (Sonnenlauf) und "Polarstreifen" (Mondlauf) ist, dass sich dieser Streifen in einer \(18,6\)-Jahres-Periode bewegt (siehe Bild 5). Diese Seite wird, wie schon weiter oben erklärt wurde, zum Zeitpunkt einer Großen Mondwende veröffentlicht. Der "Polarstreifen" befindet sich demnach maximal südlich auf \(~[~60,45°,~62,35°]~\).  Ein Beobachter müsste sich also beispielsweise nach Alaska, Skandinavien oder auf die Färöer-Inseln aufmachen, um dieses seltene Ereignis erleben zu können.

Die Angaben zum "Polarstreifen" wurden nur für die Nordhalbkugel gemacht. Für die Südhalbkugel geht man einfach von  φ  zu  -φ  über.


Zusammenfassung der wichtigsten Ergebnisse für den Erdmond
  •  Die Deklination \(~\delta~\) des Mondes ändert sich periodisch mit der Periodenlänge \(~27,3\) Tage (siderischer Monat) zwischen den Extremen \(-\delta_{max}~\) und \(+\delta_{max~}\).

  •  \(\delta_{max~}\) ändert sich periodisch mit der Periodenlänge \(~18,6\) Jahre zwischen den Extremen \(~18,3°\) und \(~28,6°\).

  •  Die Phänomene "Mond geht auf und unter", "Mond bleibt unsichtbar" und "Mond ist dauerhaft sichtbar" sind ähnlich wie bei der Sonne, mit zwei Ausnahmen:

  •        —  Die Grenzen der Polarregionen wandern mit der Periodenlänge von \(~18,6\) Jahren über einen Breitenbereich von \(~10,3°\).

  •        —  Es gibt zwei schmale Streifen am Südrand der Nordpolarregion und am Nordrand der Südpolarregion, in denen nur die Phänomene "Mond geht auf und unter" und "Mond bleibt unsichtbar" auftreten.


Aufgabe 7

o   In welchen Regionen des Planeten ist der jeweilige Mond (siehe folgende Liste) unsichtbar? Berechnen Sie dazu \(_~\beta_~\) und den %-Wert für die Kugelkappe wie in Aufgabe 1:

Marsmonde Phobos und Deimos
Die vier Galileischen Jupitermonde
Saturnmond Titan

Die Werte \(_~a_~\) und \(_~r_~\) (siehe Aufgabe 1) für die genannten Planeten und Monde entnimmt man einschlägigen Tabellen.

Planet Mond \(\beta\) beschienen  
Mars Phobos \(21,2°\) \(31,9~\%\) \(1,1°\) Bahnneigung
  Deimos \(8,3°\) \(42,8~\%\) kleinster
Jupiter Io \(9,4°\) \(41,8~\%\)  
  Europa \(5,9°\) \(44,9~\%\)  
  Ganymed \(3,7°\) \(46,8~\%\) größter
  Kallisto \(2,1°\) \(48,2~\%\)  
Saturn Titan \(2,7°\) \(47,7~\%\)  

Die fünf in der Tabelle aufgeführten Monde von Jupiter und Saturn sind im Vergleich zu den vielen anderen Monden in unserem Sonnensystem riesig, sie nehmen zusammen mit unserem Erdmond die Plätze 1 bis 6 ein; Ganymed ist der größte von allen, Deimos ist der kleinste in der Tabelle. Die Marsmonde sind winzig. Der innere und größere Mond Phobos hat von allen hier aufgeführten Monden die größte (aber doch sehr kleine) Bahnneigung gegenüber dem Äquator; er ist dem Mars so nahe, dass man ihn nur zwischen den Breitengraden ca. \(\pm 70°\) sehen kann. Der äußerste Galileische Jupitermond Kallisto ist dagegen fast überall vom Jupiter aus sichtbar.

Weblinks

Prähistorische Astronomie mit Erläuterung zu den Mondwenden

Wikipedia :  Bahngestalt   Bahnperiode   Mondbahn

Mondphasenkalender mit tagesgenauer Deklination


Ergänzender Blogbeitrag (# 42) zu dieser Problemseite.


Kategorie: Geomathematik

Publiziert 2025-06-30          Stand 2026-01-16

voriges Problem   |   Liste aller Probleme mit Lösungen   |    nächstes Problem

Manfred Börgens   |    zur Leitseite