Auch im Herbst gibt es noch Blüten. Wir wollen sie nach einem bestimmten Muster zeichnen. Das soll in zwei Schritten geschehen:
1. Schritt: Um einen Einheitskreis wird ein Kranz von n gleich großen Kreisen gelegt, die alle den Einheitskreis berühren und sich gegenseitig berühren. Diese sollen hier "äußere Blütenblätter" heißen.
Die Mittelpunkte der äußeren Blütenblätter liegen also auf einem regelmäßigen n-Eck; dies gilt auch für die beiden Ketten der Berührpunkte.
2. Schritt: Nun wird in die Mitte der äußeren Blütenblätter wieder ein Einheitskreis gelegt, um den genau wie im 1. Schritt ein Kranz von m Kreisen gelegt wird, die wir "innere Blütenblätter" nennen.
Das Ergebnis der beiden Schritte sieht man in Bild 1; dort ist n = 4, m = 9 . Die Einheitskreise sind grün gefüllt. Die inneren Blütenblätter wurden nur in eines der äußeren Blütenblätter gezeichnet, die anderen erhalten natürlich die gleiche Füllung.
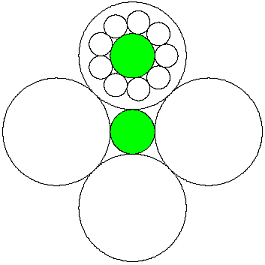
Bild 1
1. Frage: Wie groß ist der Radius der äußeren und inneren Blütenblätter?
2. Frage: Für welche Paare (n, m) ist die Anordnung möglich?
Lösung