Schachteln und Kugeln

Nachdem das vorige Problem etwas mehr Aufwand erforderte, gibt es diesmal eines mit einer einfachen Lösung.

Es sind  m  Kugeln auf  n  Schachteln zu verteilen. Es sei  m ≥ 1  und  n ≥ 2 . Die Verteilung soll so erfolgen, dass alle Anzahlen von Kugeln in den Schachteln paarweise verschieden sind. Es ist dabei erlaubt, dass eine Schachtel leer bleibt.

Hier ist ein Beispiel für  n = 4  und  m = 12 :




Welche Werte darf  m  annehmen, wenn  n  vorgegeben wird ?

Welche Werte darf  n  annehmen, wenn  m  vorgegeben wird ?

Lösung

Der Einfachheit halber verteilen wir die Kugeln so, dass die Schachteln von links nach rechts mit ansteigenden Anzahlen von Kugeln bestückt sind. Für das Beispiel aus der Aufgabenstellung sieht das dann so aus:



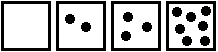
Eigentlich kann man schon jetzt erkennen, wie man zu einer Lösung kommt: Statt  0, 2, 3, 7  Kugeln hätten auch  0, 1, 2, 3  Kugeln gereicht.

Wir denken uns die Schachteln von links nach rechts nummeriert mit  i = 1, 2, ... n ;  die Anzahl der Kugeln wird entsprechend mit  m₁, m₂, ... m_n  bezeichnet. Im Beispiel oben wäre also  m₄ = 7 .

m_i < m_i+1  und  m₁ ≥ 0    ⇒   m_i ≥ i-1  (induktiv)    ⇒   m = Σ_i=1..n m_i ≥ (n-1)n/2

Bis hierhin wurde gezeigt: Wenn alle Anzahlen von Kugeln in den Schachteln paarweise verschieden sind, dann muss  m ≥ (n-1)n/2  sein. Die Umkehrung gilt aber auch: Ist  m ≥ (n-1)n/2 ,  so ist es möglich, dass alle Anzahlen paarweise verschieden sind. Denn bestückt man die ersten  n-1  Schachteln mit  m_i = i-1  Kugeln, also mit  0, 1, 2, ... n-2  Kugeln (das sind insgesamt  (n-2)(n-1)/2 ) ,  dann bleiben für die  n-te Schachtel noch  m -(n-2)(n-1)/2 ≥ (n-1)n/2 -(n-2)(n-1)/2 = n-1  Kugeln übrig, also mindestens  n-1 .

Damit ist die erste Frage beantwortet:

Hat man  n  Schachteln, so benötigt man mindestens (n-1)n/2  Kugeln.  Alle  m ≥(n-1)n/2  führen zu einer erlaubten Verteilung der Kugeln.

Für die zweite Frage lösen wir die Ungleichung  m ≥(n-1)n/2  nach  n  auf:

n² - n - 2m ≤ 0
     →     die positive Nullstelle von  n² - n - 2m  ist  1/2 + (1/4 + 2m)^1/2
     →     wegen  n  ganzzahlig kommen also alle  n  mit  2 ≤ n ≤ [1/2 + (1/4 + 2m)^1/2]  in Frage  ( [..] für Abrundung)

Hat man  m  Kugeln, so darf es höchstens  [1/2 + (1/4 + 2m)^1/2]  Schachteln geben.  Alle  n ≤ [1/2 + (1/4 + 2m)^1/2]  führen zu einer erlaubten Verteilung der Kugeln.

Beispiel: Für  42  Kugeln ist  9  die maximale Anzahl der Schachteln. Im nächsten Bild sieht man warum. Die  6  grünen Kugeln würden nicht mehr für eine  10. Schachtel ausreichen.





Dieses Problem ist eine Erweiterung der Aufgabe 1/2, # 2 in Mathematical Excalibur.

Publiziert 2020-03-25          Stand 2017-01-03

voriges Problem   |   Liste aller Probleme mit Lösungen   |    nächstes Problem