| Manfred Börgens Mathematische Probleme # 109 |
Liste aller Probleme mit Lösungen voriges Problem nächstes Problem |
zur Leitseite |
16 Räuber
Zunächst ging alles gut. Die 17 Räuber konnten die fette Beute in Sicherheit bringen. Sie lagerte seitdem in einem Tresor, der gut versteckt wurde. Der Anführer der Räuber (er zählt mit unter die 17 , also nicht wie bei Jim Knopf und die Wilde 13 ) sicherte den Tresor mit einer 80-stelligen Zahlenkombination. Aus Sicherheitsgründen nummerierte er die 16 anderen Räuber von 0 bis 15 und gab jedem nur einen Fünferblock des Codes zum Auswendiglernen - Räuber 0 erhielt die ersten 5 Ziffern, Räuber 1 die nächsten 5 Ziffern usw.
Aber dann ging alles schief. Die Räuber wurden von der Polizei gefasst. Der Anführer überlebte die Schießerei nicht. Die anderen 16 Räuber kamen ins Gefängnis. Die Polizei fand die Beute nicht.
Die 16 Räuber wurden in dasselbe Gefängnis gesperrt, alle in verschiedene Zellen. Nur beim täglichen Hofgang konnten sie miteinander sprechen. Diese Hofgänge waren zwar nur kurz, aber sie reichten aus, um eine Verabredung zu treffen. Sie hofften, dass einer von ihnen begnadigt würde oder ausbrechen könnte. Derjenige sollte dann ganz rasch die Beute holen und sicher aufbewahren, da der Tresor schon ziemlich lange unbewacht geblieben war und jederzeit entdeckt werden könnte.
Also mussten alle Räuber möglichst schnell den gesamten 80-stelligen Code lernen. Die Räuber waren übereingekommen, bei jedem Hofgang (also einmal am Tag) 8 Paare zu bilden (jeden Tag andere), die sich gegenseitig über alles austauschen sollten, was sie bis dahin in Erfahrung gebracht hatten.
n sei die Anzahl der Räuber. Aus der Fragestellung geht hervor, dass es sich um eine Zweierpotenz n = 2m handelt, mit m ∈ N . n ist außerdem die Anzahl der einzelnen und disjunkten Informationen (also hier fünfstellige Ziffernblöcke), die zusammengeführt werden sollen. Der Umfang des Informationsgehalts, der anfangs bei den einzelnen Räubern gespeichert ist (Ziffernblöcke), spielt für unser Problem keine Rolle. Wir geben den Räubern die Nummern 0, ..., 2m - 1 ; die bei den einzelnen Räubern gesammelten Informationen drücken wir als Mengen aus: Wenn beispielsweise beim ersten Hofgang Räuber 2 mit Räuber 10 spricht, so sind danach beide im Besitz der Informationsmenge {2,10}. Abkürzend soll Mi,j für die Informationsmenge des i-ten Räubers nach dem j-ten Hofgang stehen, mit Mi,0 = {i} vor dem ersten Hofgang; im Beispiel wäre dann M2,1 = M10,1 = {2,10}.
Nach m Hofgängen ist offenbar jeder einzelne Räuber im Besitz von maximal n = 2m Informationen. 16 Räuber benötigen somit mindestens 4 Hofgänge für den Informationsaustausch. Nun soll gezeigt werden, dass m Hofgänge auch hinreichend sind.
Es muss also gezeigt werden, dass Mi,m = {0, ..., n-1} für alle i gilt. Anders ausgedrückt: m Hofgänge sind genau dann hinreichend, wenn sich die Informationsmenge jedes Räubers bei jedem Hofgang verdoppelt, d.h. |Mi,j| = 2·|Mi,j-1| für j = 1, ..., m . Das kann nur dann geschehen, wenn bei jedem Hofgang nur Paare {i1,i2} von Räubern miteinander sprechen, deren Informationsmengen disjunkt sind: Mi1,j ∩ Mi2,j = Ø. Der Beweis, dass m Hofgänge hinreichend sind, geht nun leicht mit vollständiger Induktion über m :
m = 1 n = 2 Räuber haben vor dem Hofgang die Informationsmengen M0,0 = {0} bzw. M1,0 = {1} und nachher M0,1 = M1,1 = {0,1}. Also reicht ein Hofgang aus.
m → m+1 Man kann für n = 2m+1 Räuber zunächst in Worten beschreiben, was passiert: n/2 Räuber suchen sich beim ersten Hofgang andere n/2 Räuber als Gesprächspartner. Für beide Gruppen gilt jeweils: Nach dem Hofgang sind insgesamt alle n Informationen vorhanden, und zwar in jeweils n/2 disjunkten Paaren. Nun ist aber n/2 = 2m, und nach Induktionsvoraussetzung lassen sich in beiden Gruppen alle Informationsmengen in weiteren m (also insgesamt m+1) Hofgängen bei jedem der Räuber zusammenführen. - Man beachte, dass der Umfang der Ursprungsinformationen bei dieser Argumentation keine Rolle spielt; in den beiden Gruppen treten nach dem ersten Hofgang Paare von Räubernummern an die Stelle von einzelnen Nummern. - Das Ganze lässt sich natürlich auch formal beschreiben: n = 2m+1 Räuber haben vor dem ersten Hofgang die Informationsmengen M0,0 = {0}, ..., Mn-1,0 = {n-1}. Beim ersten Hofgang bilden sich n/2 = 2m Paare, die jeweils ihre Informationen austauschen. Diese Paare (bzw. die zugehörigen Informationsmengen nach dem Hofgang) kann man mit Mpr,1 = Mqr,1 = {pr,qr} für r = 1, ..., n/2 bezeichnen; für die Vereinigungsmenge gilt ∪r{pr,qr} = {0, ..., n-1}, also ist in beiden Gruppen (Räuber pr und Räuber qr) jeweils die komplette Information verfügbar. Für die Induktionsvoraussetzung haben wir also zwei Gruppen mit jeweils 2m Räubern, bei denen Mppr,0 = {pr,qr} bzw. Mqqr,0 = {pr,qr} den neuen Anfangszustand beschreibt; somit ergibt sich in beiden Gruppen für jeden Räuber eine Zusammenführung der Informationen auf ∪r{pr,qr} = {0, ..., n-1} in m Schritten.
Damit können wir die erste Frage beantworten:
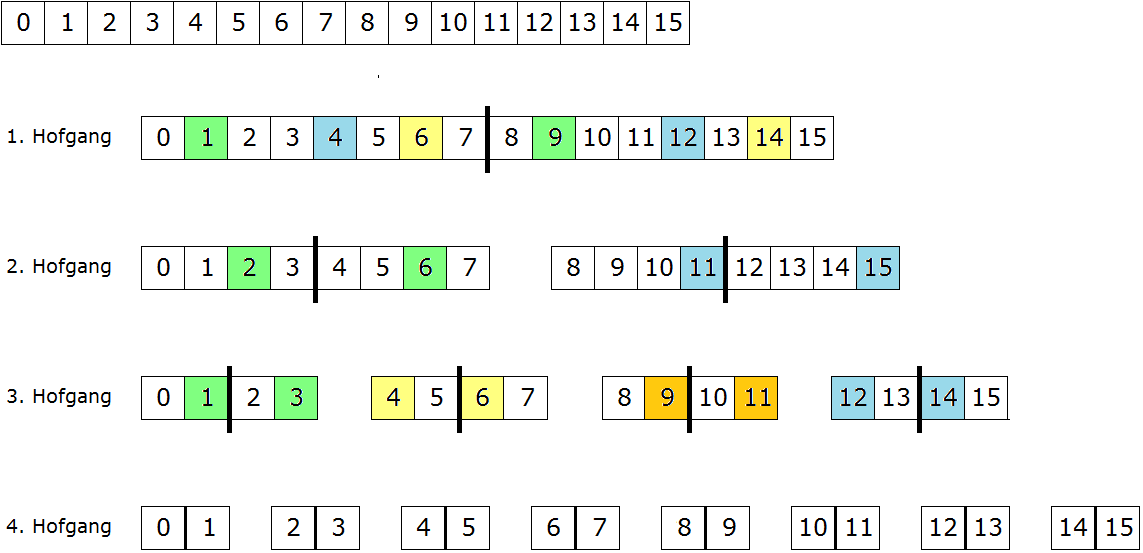
| Der Kern der Lösung: Vor jedem Hofgang teilen sich alle Gruppen in jeweils zwei Hälften, so dass die Räuber beim j. Hofgang 2j Gruppen bilden. Die Kommunikation erfolgt nur zwischen zusammengehörigen Hälften. Dann ist jede Gruppe nach dem j. Hofgang im Besitz der kompletten Information, die sich disjunkt und gleichmäßig auf ihre 2m-j Mitglieder verteilt. |
Die in der Graphik gewählte Gruppeneinteilung führt zu einem einfachen Algorithmus, der beschreibt, wer mit wem beim j. Hofgang spricht.
Auf den ersten Blick erscheint das nicht so einfach zu ein. Nehmen wir den Räuber # 6 . Er spricht nacheinander mit 14, 2, 4, 7 . Da ist zunächst nur schwer eine Regel erkennbar.
Wenn man die 2m Räuber aufsteigend sortiert wie in der Graphik, erhält man die folgende Systematik:
(1) j. Hofgang: 2j Gruppen mit jeweils 2m-j Räubern
k. Gruppe: Räuber i = (k-1)·2m-j, ..., k·2m-j - 1
k ungerade ⇔ i spricht mit i + 2m-j
k gerade ⇔ i spricht mit i - 2m-j
Es werden also für die Hofgespräche die Gruppen mit ungeradem k den Gruppen mit dem nachfolgenden geraden k zugeordnet (also sprechen die Räuber in der 1. Gruppe mit denen in der 2. Gruppe, die Räuber in der 3. Gruppe mit denen in der 4. Gruppe usw.). - Wie sieht man, dass jede dieser Gruppen beim (j+1). Hofgang in zwei Hälften geteilt werden, die dann miteinander sprechen - so wie oben im "Kern der Lösung" beschrieben? Nehmen wir die k. Gruppe aus (1). Beim nächsten Hofgang wird aus i = (k-1)·2m-j, ..., k·2m-j - 1 - da es sich jetzt um den (j+1). Hofgang handelt - i = (2k-2)·2m-j-1, ..., 2k·2m-j-1 - 1 ; teilt man dies in zwei gleiche Hälften, erhält man i = (k1-1)·2m-j-1, ..., k1·2m-j-1 - 1 und i = k1·2m-j-1, ..., (k1+1)·2m-j-1 - 1 mit k1 = 2k - 1 ungerade, also tatsächlich eine "ungerade" und eine "gerade" Gruppe.
Wie kann man nun die Nummern der Räuber in den ungeraden Gruppen von denen in den geraden Gruppen unterscheiden, um den Räubern ihre Aufgane zu erleichtern? Wir betrachten zunächst Beispiele aus der Graphik.
j = 3 Vor dem 3. Hofgang gibt es vier Gruppen, beginnend mit {0,1,2,3}. In jeder der vier Gruppen sprechen die kleineren Nummern mit den größeren. Um das einfach darzustellen, muss man lediglich die Nummern mod 4 nehmen, damit hat jede Gruppe die Gestalt {0,1,2,3}. Der Rest ist dann leicht: Ist diese Nummer < 2 , so spricht sie mit der um 2 größeren Nummer; ist sie ≥ 2 , so spricht sie mit der um 2 kleineren Nummer. - Beispiel: 12 spricht mit 14: 12 mod 4 = 0 < 2 , also spricht 12 mit 12 + 2 = 14 ; 14 mod 4 = 2 ≥ 2 , also spricht 14 mit 14 - 2 = 12 .
Wir schauen uns das noch für j = 2 an. Hier nehmen wir die Nummern mod 8 und teilen diese nach < 4 und ≥ 4 . - Beispiel: 10 spricht mit 14: 10 mod 8 = 2 < 4 , also spricht 10 mit 10 + 4 = 14 ; 14 mod 8 = 6 ≥ 4 , also spricht 14 mit 14 - 4 = 10 .
Ausgehend von diesen Beispielen lässt sich nun eine allgemeine Regel für den i. Räuber beim j. Hofgang aufstellen.
Publiziert 2019-12-28 Stand 2016-07-11
voriges Problem | Liste aller Probleme mit Lösungen | nächstes Problem