Die Lösung steht im unteren Teil der Seite.
Der 4-Farben-Satz für Landkarten in der Ebene oder auf einer Kugel ist weithin bekannt. Er wurde 1977 bewiesen. Bereits vorher kannte man Beweise für den 6-Farben-Satz auf dem Möbiusband und den 7-Farben-Satz auf dem Torus. Um den letzteren soll es hier gehen.
Jede Landkarte auf dem Torus lässt sich mit 7 Farben so färben, dass benachbarte Länder nie die gleiche Farbe haben. Mit weniger Farben geht es nicht. In Bild 1 sieht man einen Torus mit 7 Ländern, deren Färbung 7 Farben erfordert, weil jedes Land an alle anderen Länder grenzt.

Bild 1
Nun zeigt Bild 1 zwar eine schöne und gut überprüfbare Anordnung der 7 Länder, aber es fällt nicht leicht, ein bestimmtes Prinzip zu erkennen oder sich diese Anordnung zu merken. Wir wollen eine einfache Konstruktion angeben, die man jederzeit leicht reproduzieren kann, ohne einen Torus zeichnen zu müssen. Diese Konstruktion soll es jedem sofort einsichtig machen, warum man bei Landkarten auf dem Torus im Allgemeinen nicht mit weniger als 7 Farben auskommt.
Die Gestalt des Torus ist für den 7-Farben-Satz weitgehend unerheblich. Der Satz gilt für die Oberfläche jedes Körpers vom Geschlecht 1, also anschaulich gesprochen für Körper mit genau einem Loch. Wenn man beispielsweise eine Landkarte auf eine Tasse mit einem Henkel zeichnen würde, könnte man die Tasse und die Länder topologisch (d.h. durch vorsichtiges Kneten) zu einem Torus verformen, so dass die Nachbarschaften zwischen den Ländern erhalten blieben. Also gilt der 7-Farben-Satz auch für einhenklige Tassen.
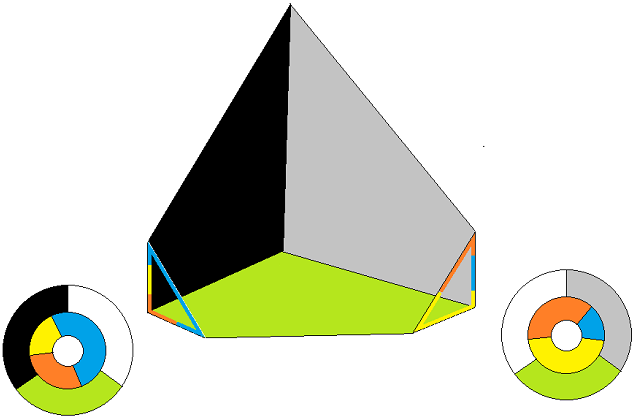
Unsere Konstruktion beginnt mit einem Tetraeder. Seine Oberfläche besteht aus 4 Dreiecken. Im linken Teil von Bild 2 schauen wir in den Tetraeder hinein, d.h. die Ecke A ist hinten unten, also die am weitesten vom Betrachter entfernte Ecke. An A grenzen 3 Farben an: Grün, Grau und Schwarz. Die vierte, vordere Seite des Tetraeders kann man sich - da wir ja in den Tetraeder hineinschauen - als Glasscheibe vorstellen (gleich vor dem Betrachter und gegenüber der Ecke A). Als vierte Farbe wählen wir also Transparent.
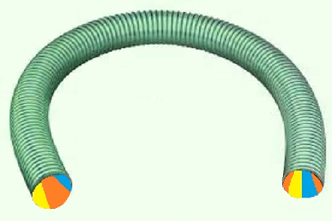
Und nun bohren wir ein Loch durch den Tetraeder. Dazu schneiden wir an der linken und der rechten unteren Ecke ein Stück ab; das sieht man rechts in Bild 2. Die beiden kleinen dreieckigen Öffnungen - und ab hier wird nichts mehr gezeichnet, man muss es sich vorstellen - werden durch einen Schlauch verbunden, der leicht gebogen durch das Innere des Tetraeders verläuft, ohne die Seitenflächen zu berühren. Der linke und der rechte Austritt des Schlauchs ist dreieckig, aber weiter innen kann man ihn sich gerne verformt als rohrartig vorstellen.
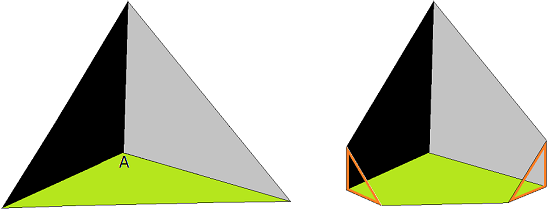
Bild 2
Der durchbohrte Tetraeder ist topologisch äquivalent zum Torus, weil er genau ein Loch hat. Bei ihm kann man sich noch leichter als bei der Henkeltasse vorstellen, wie die Verformung durchgeführt wird.
Jetzt kommt der 7-Farben-Satz: 4 Farben sind schon auf der Oberfläche des Tetraeders vergeben, also wird der Schlauch mit 3 weiteren Farben gefärbt, so dass insgesamt 7 Länder entstehen. Die 3 Schlauchfarben werden (so viel wird verraten) einfach in langen Streifen vom linken zum rechten Austritt des Schlauchs aufgetragen. Sie müssen natürlich nicht exakt parallel oder gleich breit sein.
Vorsicht: Die 3 Farbstreifen dürfen nicht mit den Seiten der Dreiecke bei den Austritten (orange in Bild 2 rechts) zusammenfallen, auch nicht zyklisch verdreht. Warum nicht ?
Aber man darf natürlich den Schlauch so verdrehen und dehnen, dass einzelne Schlauchfarben eine oder mehrere Ecken der kleinen Dreiecke einschließen.
Falls man sich den Schlauch nicht gut vorstellen kann, findet man hier ein Bild, das später auch in der Lösung verwendet wird.
Wie muss der Schlauch gefärbt werden, so dass jedes der 7 Länder auf dem durchbohrten Tetraeder an alle anderen Länder grenzt ?