Vor 20 Jahren bewies Thomas Hales die Keplersche Vermutung.
Die hier vorgestellten Probleme hängen eng mit der Keplerschen Vermutung zusammen. Johannes Kepler formulierte 1611 das Prinzip der dichtesten Kugelpackung, nach dem die raumsparendste Anordnung gleichartiger Kugeln genau die ist, die man auch intuitiv anwenden würde, damals etwa für Kanonenkugeln und heute für Apfelsinen.
Das Grundprinzip ist dabei einfach: Man legt die Kugeln in Schichten übereinander; jede Kugel ruht in einer Vertiefung, die durch drei oder vier darunter liegende Kugeln gebildet wird, so wie im folgenden Bild.
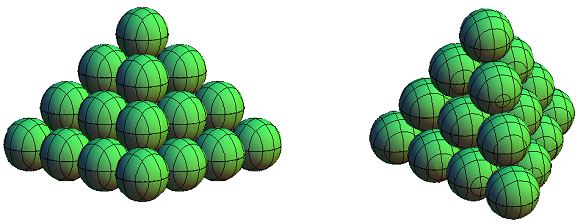
Bild 1
Links in Bild 1 sind die Kugeln in jeder Ebene quadratisch angeordnet, rechts dreieckig. Schematisch lassen sich die Ebenen wie in Bild 2 darstellen:
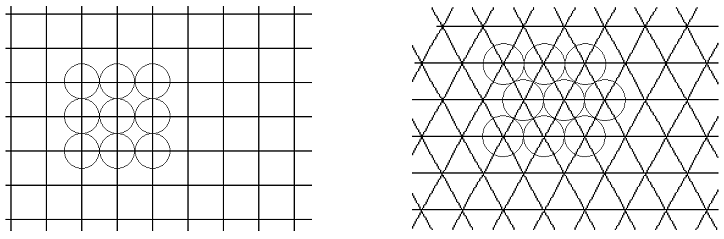
Bild 2
Die Keplersche Vermutung blieb fast 400 Jahre unbewiesen und zählte zu den größten und bekanntesten Herausforderungen in der Mathematik. Ihr besonderer Reiz bestand in der sehr anschaulichen und auch mathematischen Laien verständlichen Problemstellung. Im August 1998, also vor 20 Jahren, publizierte Thomas Hales einen Beweis, der sich stark auf umfangreiche Computerprogramme stützt und seither mehrfach und auf verschiedenen Wegen verifiziert wurde.
Die Aufgabenstellungen auf dieser Seite betreffen vor allem Kugelpyramiden wie in Bild 1. Die beiden Pyramiden wollen wir unterscheiden durch die Begriffe Kugel-Halboktaeder (links in Bild 1) und Kugel-Tetraeder (rechts in Bild 1). Beginnen wollen wir mit der quadratischen Anordnung, jeweils links in Bild 1 und Bild 2. Die Stapelung der Ebenen ist in Bild 3 dargestellt.




Bild 3
Im Folgenden soll n die Anzahl der Schichten in der Pyramide sein, also hier im Kugel-Halboktaeder. Die Schichten sollen von oben nach unten mit j = 1 ... n gezählt werden. Im folgenden Bild 4 sieht man, wie für n = 6 die 3. Schicht auf die 4. - 6. Schicht gelegt wird.

Bild 4
Für die Aufgaben auf dieser Seite sollen alle Kugeln den Durchmesser 1 haben.
Aufgabe 1
Wieviele Kugeln enthält eine Pyramide (Kugel-Halboktaeder) mit n Schichten?
Aufgabe 2
Wie hoch ist eine Pyramide (Kugel-Halboktaeder) mit n Schichten?
Aufgabe 3
Wie groß ist die Kusszahl in der quadratischen Kugelanordnung?
Unter der Kusszahl versteht man die Anzahl der Kugeln, die an eine Kugel anstoßen. Dafür denken wir uns die Pyramide nach allen Richtungen fortgesetzt; es gibt also keine Kugeln "am Rand", der ganze Raum soll mit Kugeln angefüllt sein.
Aufgabe 4
Wie groß ist die Packungsdichte in der quadratischen Kugelanordnung?
Hier geht es jetzt also um die Keplersche Vermutung. Wir denken uns die Pyramide nach allen Richtungen fortgesetzt; d.h. der ganze Raum soll mit Kugeln angefüllt sein. Unter Packungsdichte versteht man den Anteil des Raums, den die Kugeln einnehmen.
Nun kommen wir zur dreieckigen Anordnung wie rechts in den Bildern 1 und 2. Bild 5 zeigt den Aufbau eines Kugel-Tetraeders für n = 4 .
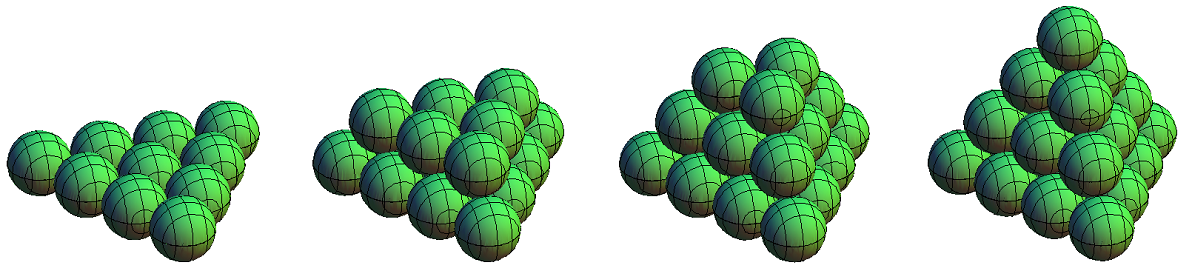
Bild 5
Aufgabe 5
Wieviele Kugeln enthält die j. Schicht einer Pyramide (Kugel-Tetraeder)?
Aufgabe 6
Wieviele Kugeln enthält eine Pyramide (Kugel-Tetraeder) mit n Schichten?
Aufgabe 7
Wie hoch ist eine Pyramide (Kugel-Tetraeder) mit n Schichten?
Aufgabe 8
Bei der dreieckigen Kugelanordnung sei die Pyramide nach allen Richtungen fortgesetzt; d.h. der ganze Raum soll mit Kugeln angefüllt sein. Zeigen Sie, dass es dann für die "Schichtung" der einzelnen Ebenen (im Wesentlichen) zwei verschiedene Möglichkeiten gibt, die man anschaulich mit ABABAB und ABCABC beschreiben kann.
Welche der beiden Möglichkeiten wurde in Bild 5 angewandt?
Aufgabe 9
Wie groß ist die Kusszahl in der dreieckigen Kugelanordnung?
Aufgabe 10
Wie groß ist die Packungsdichte in der dreieckigen Kugelanordnung?
Aufgabe 11
Vergleichen Sie Resultate der Aufgaben 3 und 9 sowie der Aufgaben 4 und 10. Wie lässt sich das Ergebnis dieses Vergleichs erklären?
Welche Rolle spielen dabei die beiden verschiedenen Anordnungen aus Aufgabe 8?
Lösung