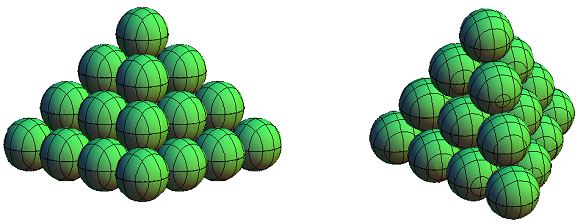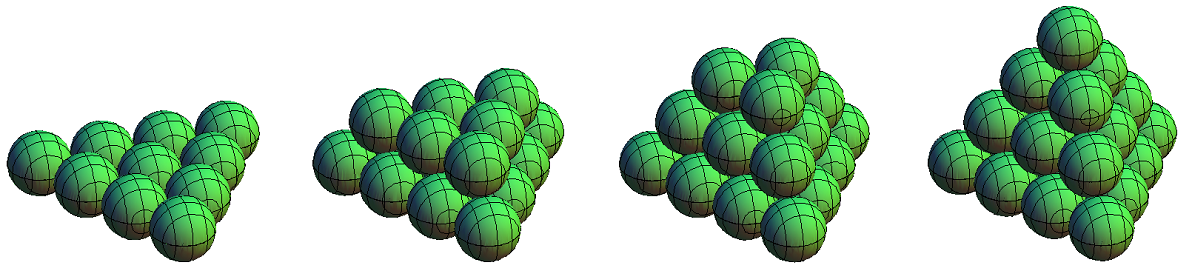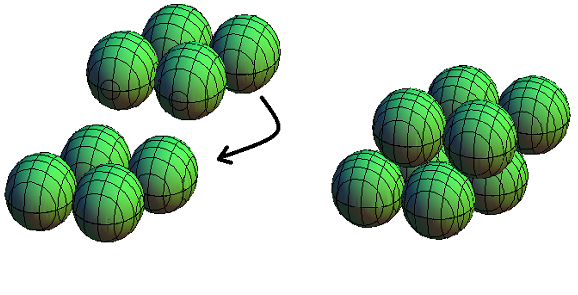Kugelpyramiden
Vor 20 Jahren bewies Thomas Hales die Keplersche Vermutung.
Die Lösung steht im unteren Teil der Seite.
Die hier vorgestellten Probleme hängen eng mit der Keplerschen Vermutung zusammen. Johannes Kepler formulierte 1611 das Prinzip der dichtesten Kugelpackung, nach dem die raumsparendste Anordnung gleichartiger Kugeln genau die ist, die man auch intuitiv anwenden würde, damals etwa für Kanonenkugeln und heute für Apfelsinen.
Das Grundprinzip ist dabei einfach: Man legt die Kugeln in Schichten übereinander; jede Kugel ruht in einer Vertiefung, die durch drei oder vier darunter liegende Kugeln gebildet wird, so wie im folgenden Bild.
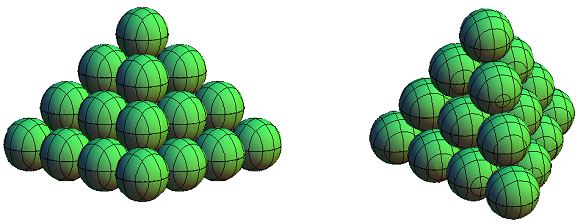
Bild 1
Links in Bild 1 sind die Kugeln in jeder Ebene quadratisch angeordnet, rechts dreieckig. Schematisch lassen sich die Ebenen wie in Bild 2 darstellen:
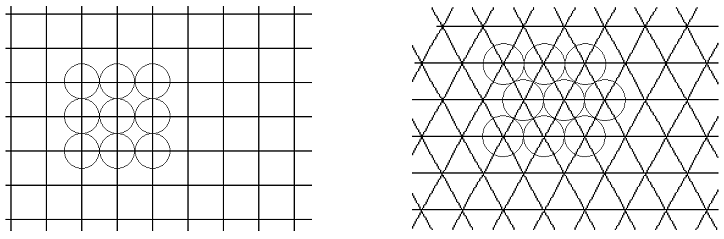
Bild 2
Die Keplersche Vermutung blieb fast 400 Jahre unbewiesen und zählte zu den größten und bekanntesten Herausforderungen in der Mathematik. Ihr besonderer Reiz bestand in der sehr anschaulichen und auch mathematischen Laien verständlichen Problemstellung. Im August 1998, also vor 20 Jahren, publizierte Thomas Hales einen Beweis, der sich stark auf umfangreiche Computerprogramme stützt und seither mehrfach und auf verschiedenen Wegen verifiziert wurde.
Die Aufgabenstellungen auf dieser Seite betreffen vor allem Kugelpyramiden wie in Bild 1. Die beiden Pyramiden wollen wir unterscheiden durch die Begriffe Kugel-Halboktaeder (links in Bild 1) und Kugel-Tetraeder (rechts in Bild 1). Beginnen wollen wir mit der quadratischen Anordnung, jeweils links in Bild 1 und Bild 2. Die Stapelung der Ebenen ist in Bild 3 dargestellt.




Bild 3
Im Folgenden soll n die Anzahl der Schichten in der Pyramide sein, also hier im Kugel-Halboktaeder. Die Schichten sollen von oben nach unten mit j = 1 ... n gezählt werden. Im folgenden Bild 4 sieht man, wie für n = 6 die 3. Schicht auf die 4. - 6. Schicht gelegt wird.

Bild 4
Für die Aufgaben auf dieser Seite sollen alle Kugeln den Durchmesser 1 haben.
Aufgabe 1
Wieviele Kugeln enthält eine Pyramide (Kugel-Halboktaeder) mit n Schichten?
Aufgabe 2
Wie hoch ist eine Pyramide (Kugel-Halboktaeder) mit n Schichten?
Aufgabe 3
Wie groß ist die Kusszahl in der quadratischen Kugelanordnung?
Unter der Kusszahl versteht man die Anzahl der Kugeln, die an eine Kugel anstoßen. Dafür denken wir uns die Pyramide nach allen Richtungen fortgesetzt; es gibt also keine Kugeln "am Rand", der ganze Raum soll mit Kugeln angefüllt sein.
Aufgabe 4
Wie groß ist die Packungsdichte in der quadratischen Kugelanordnung?
Hier geht es jetzt also um die Keplersche Vermutung. Wir denken uns die Pyramide nach allen Richtungen fortgesetzt; d.h. der ganze Raum soll mit Kugeln angefüllt sein. Unter Packungsdichte versteht man den Anteil des Raums, den die Kugeln einnehmen.
Nun kommen wir zur dreieckigen Anordnung wie rechts in den Bildern 1 und 2. Bild 5 zeigt den Aufbau eines Kugel-Tetraeders für n = 4 .
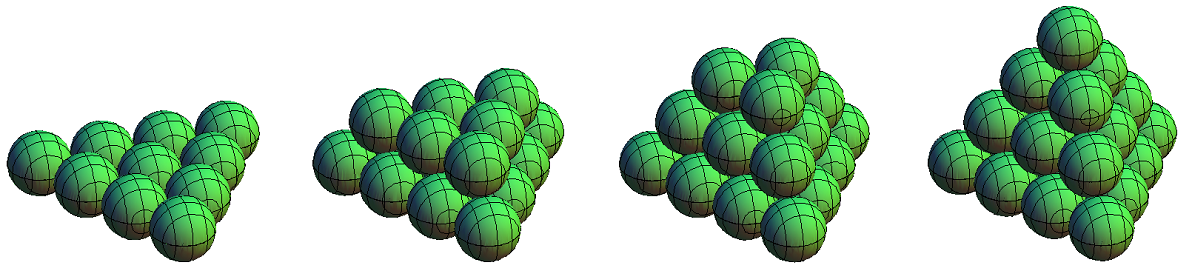
Bild 5
Aufgabe 5
Wieviele Kugeln enthält die j. Schicht einer Pyramide (Kugel-Tetraeder)?
Aufgabe 6
Wieviele Kugeln enthält eine Pyramide (Kugel-Tetraeder) mit n Schichten?
Aufgabe 7
Wie hoch ist eine Pyramide (Kugel-Tetraeder) mit n Schichten?
Aufgabe 8
Bei der dreieckigen Kugelanordnung sei die Pyramide nach allen Richtungen fortgesetzt; d.h. der ganze Raum soll mit Kugeln angefüllt sein. Zeigen Sie, dass es dann für die "Schichtung" der einzelnen Ebenen (im Wesentlichen) zwei verschiedene Möglichkeiten gibt, die man anschaulich mit ABABAB und ABCABC beschreiben kann.
Welche der beiden Möglichkeiten wurde in Bild 5 angewandt?
Aufgabe 9
Wie groß ist die Kusszahl in der dreieckigen Kugelanordnung?
Aufgabe 10
Wie groß ist die Packungsdichte in der dreieckigen Kugelanordnung?
Aufgabe 11
Vergleichen Sie Resultate der Aufgaben 3 und 9 sowie der Aufgaben 4 und 10. Wie lässt sich das Ergebnis dieses Vergleichs erklären?
Welche Rolle spielen dabei die beiden verschiedenen Anordnungen aus Aufgabe 8?
Lösung
Aufgabe 1
Wieviele Kugeln enthält eine Pyramide (Kugel-Halboktaeder) mit n Schichten?
In der j. Schicht liegen j2 Kugeln. Die Summe s der ersten n Quadratzahlen findet man in vielen Formelsammlungen; sie lässt sich leicht mittels vollständiger Induktion beweisen. Diese Summe findet man auch unter dem Namen quadratische Pyramidalzahl. Man erhält als Ergebnis:
s = n(n+1)(2n+1)/6
Aufgabe 2
Wie hoch ist eine Pyramide (Kugel-Halboktaeder) mit n Schichten?
Legt man eine Kugel in die Vertiefung der vier darunter liegenden Kugeln, so bilden die fünf Mittelpunkte der Kugeln ein Halboktaeder (quadratische Pyramide) mit Kantenlänge = 1 . Die Höhe einer solchen Pyramide beträgt 1/√2 . Also liegt jede Schicht um 1/√2 höher als die darunter liegende. Bei n Schichten erhält man für die Gesamthöhe h :
h = 1 +(n-1)/√2
Aufgabe 3
Wie groß ist die Kusszahl in der quadratischen Kugelanordnung?
Jede Kugel hat in ihrer Ebene 4 Nachbarn, siehe Bild 2. In den beiden Nachbarebenen darüber und darunter ruht sie jeweils in einer Vertiefung zwischen 4 Kugeln. Die Kusszahl k beträgt somit:
k = 12
Aufgabe 4
Wie groß ist die Packungsdichte in der quadratischen Kugelanordnung?
Wir wollen das Volumen der Leerräume zwischen den Kugeln bestimmen. Jeder Leerraum ist umgeben von 8 Kugeln, deren Mittelpunkte einen Spat bilden, siehe Bild 6:
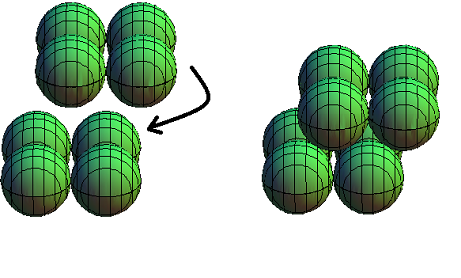
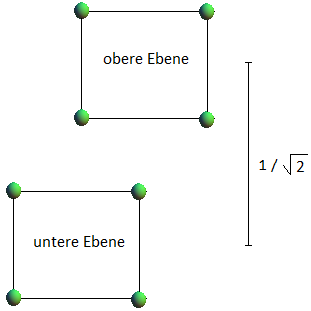
Bild 6
Nach dem Satz von Cavalieri ist das Volumen des Spats gleich Grundfläche × Höhe, also 1 × 1/√2 . In jedem Spat liegen Anteile von 8 Kugeln, die zusammen das Volumen π/6
einer ganzen Kugel haben. Die Packungsdichte p beträgt somit:
p = (π √2)/6 ≈ 0,7405
Der Raum wird also durch diese Kugelpackung zu 74,05 % ausgefüllt. Wegen Hales' Beweis wissen wir, dass sich dieser Wert nicht verbessern lässt.
Aufgabe 5
Wieviele Kugeln enthält die j. Schicht einer Pyramide (Kugel-Tetraeder)?
In der j. Schicht liegen m = 1 + 2 + ... + j Kugeln, also ist
m = j(j+1)/2
Dies sind die Dreieckszahlen, die die dritte Spalte im Pascalschen Dreieck bilden.
Aufgabe 6
Wieviele Kugeln enthält eine Pyramide (Kugel-Tetraeder) mit n Schichten?
Wir addieren die Dreieckszahlen aus der vorigen Aufgabe. Das Ergebnis kann man natürlich in Formelsammlungen finden; dies wird erleichtert, wenn man weiß, dass Dreieckszahlen oder quadratische Pyramidalzahlen (aus Aufgabe 1) wegen ihrer anschaulichen Beziehung zur Geometrie auch figurierte Zahlen heißen. – Man kann sich aber auch die kleine Mühe machen, die Summe d der Dreieckszahlen auszurechnen. Nach Aufgabe 1 ist die Summe der ersten n Quadratzahlen n(n+1)(2n+1)/6, und nach Aufgabe 5 ist die Summe der ersten n natürlichen Zahlen n(n+1)/2. Die Hälfte der Summe dieser beiden Ausdrücke liefert unser gewünschtes Ergebnis: n(n+1)(2n+4)/12 . Somit gilt:
d = n(n+1)(n+2)/6
Diese Zahlen sind als Tetraederzahlen bekannt.
Aufgabe 7
Wie hoch ist eine Pyramide (Kugel-Tetraeder) mit n Schichten?
Legt man eine Kugel in die Vertiefung der drei darunter liegenden Kugeln, so bilden die vier Mittelpunkte der Kugeln ein Tetraeder mit Kantenlänge = 1 . Die Höhe einer solchen Pyramide beträgt (√6)/3 . Also liegt jede Schicht um (√6)/3 höher als die darunter liegende. Bei n Schichten erhält man für die Gesamthöhe h :
h = 1 +(n-1)(√6)/3
Aufgabe 8
Bei der dreieckigen Kugelanordnung sei die Pyramide nach allen Richtungen fortgesetzt; d.h. der ganze Raum soll mit Kugeln angefüllt sein. Zeigen Sie, dass es dann für die "Schichtung" der einzelnen Ebenen (im Wesentlichen) zwei verschiedene Möglichkeiten gibt, die man anschaulich mit ABABAB und ABCABC beschreiben kann.
Welche der beiden Möglichkeiten wurde in Bild 5 angewandt?
Man sollte das mal selbst ausprobieren: Wenn man zwei Schichten gelegt hat, kann man auf zwei Weisen mit der dritten Schicht fortfahren. Schon die erste in die dritte Schicht gelegte Kugel entscheidet: Entweder sie liegt genau über einer Kugel der ersten (untersten) Schicht, oder eben nicht. Das soll durch Bild 7 illustriert werden:
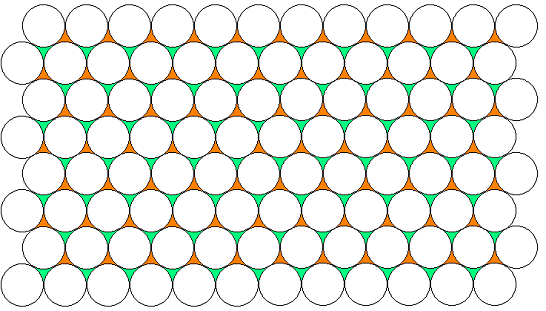
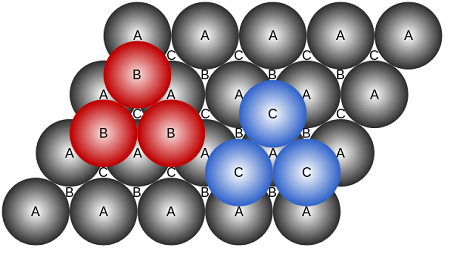
Bild 7 rechts: © Life of Riley CC BY-SA 3.0
Die linke Skizze in Bild 7 wollen wir so interpretieren, dass die weißen Kreise für eine Kugelschicht in Dreiecksanordnung stehen, und die darunter liegende Kugelschicht in den grünen Feldern durchscheint. In der rechten Skizze stehen die A-Kugeln für die weißen Kreise der linken Skizze; unter ihnen scheinen klein die Buchstaben B und C durch: Die B entsprechen den grünen Feldern links (also darunter liegenden Kugeln), die C entsprechen den orangenen Feldern links (stehen also für Lücken). Nun wird klar, wie man in der nächsten Schicht fortfahren kann: Entweder mit einer B-Schicht (rot in der rechten Skizze) oder mit einer C-Schicht (blau).
Legt man Schichten ABABAB... , so erhält man die hexagonale Kugelpackung, während ABCABC... als kubische Kugelpackung bezeichnet wird.
Natürlich kann man auch Mischformen erzeugen, z.B. ABCABAB...
Welche der beiden Möglichkeiten wurde in Bild 5 angewandt? Das lässt sich durch genaue Betrachtung des Bildes oder durch Ausprobieren mit Kugeln erkennen:
Für die Aufschichtung von Kugel-Tetraedern kommt nur die kubische Kugelpackung in Frage.
Das sieht man gut in Bild 8: Die noch fehlende Kugel in der obersten Ebene liegt nicht über einer Kugel der untersten A-Ebene.
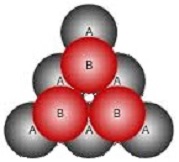
Bild 8 © Life of Riley CC BY-SA 3.0
Aufgabe 9
Wie groß ist die Kusszahl in der dreieckigen Kugelanordnung?
Jede Kugel hat in ihrer Ebene 6 Nachbarn, siehe Bild 7 links. In den beiden Nachbarebenen darüber und darunter ruht sie jeweils in einer Vertiefung zwischen 3 Kugeln. Die Kusszahl k beträgt somit:
k = 12
Aufgabe 10
Wie groß ist die Packungsdichte in der dreieckigen Kugelanordnung?
Wir wollen wie in Aufgabe 4 das Volumen der Leerräume zwischen den Kugeln bestimmen. Jeder Leerraum ist umgeben von 8 Kugeln, deren Mittelpunkte einen Spat bilden, siehe Bild 9:
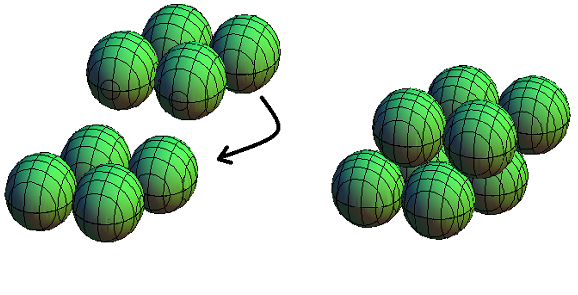
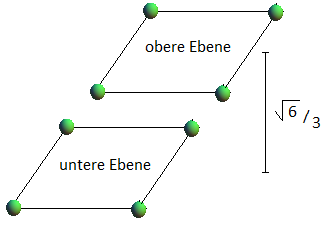
Bild 9
Nach dem Satz von Cavalieri ist das Volumen des Spats gleich Grundfläche × Höhe. Zunächst zur Grundfläche: Die Mittelpunkte je dreier benachbarter Kugeln in Bild 7 links bilden ein gleichseitiges Dreieck mit Seitenlänge 1 , also mit der Höhe (√3)/2 . Der Spat hat also als Grundfläche ein Parallelogramm mit Flächeninhalt (√3)/2 . Nach Aufgabe 7 beträgt seine Höhe (√6)/3 , was ein Volumen von 1/√2 ergibt. Analog zu Aufgabe 4 liegen in jedem Spat Anteile von 8 Kugeln, die zusammen das Volumen einer ganzen Kugel haben. Damit erhalten wir für die Packungsdichte p :
p = (π √2)/6 ≈ 0,7405
Der Raum wird also durch diese Kugelpackung ebenfalls zu 74,05 % ausgefüllt. Wegen Hales' Beweis wissen wir, dass sich dieser Wert nicht verbessern lässt.
Aufgabe 11
Vergleichen Sie Resultate der Aufgaben 3 und 9 sowie der Aufgaben 4 und 10. Wie lässt sich das Ergebnis dieses Vergleichs erklären?
Welche Rolle spielen dabei die beiden verschiedenen Anordnungen aus Aufgabe 8?
Offenbar ist die "Dichte" der Kugeln im Raum bei den beiden Varianten in Bild 1 gleich groß. Das ist kein Zufall, wie wir noch sehen werden.
Schaut man sich nur eine Schicht von Kugeln an, so wird aus Bild 2 klar, dass die Kugeln in der dreieckigen Anordnung dichter liegen als in der quadratischen Anordnung. Andererseits sinken die Kugeln in der nächsten Schicht tiefer in die Lücken zwischen jeweils vier Kugeln der quadratischen Anordnung ein als in die Lücken zwischen jeweils drei Kugeln der Dreiecksanordnung. Aber wie kommt es, dass sich die beiden Effekte gegenseitig genau aufheben, so dass sich insgesamt dieselbe Packungsdichte ergibt?
Jeder, der selbst mal Kugeln aufgeschichtet hat, kennt die Antwort:
Die kubische Kugelpackung (aus Aufgabe 8) ist identisch mit der quadratischen Kugelanordnung (aus Aufgabe 4).
Auf den ersten Blick (Bild 1) ist das verblüffend. Der Zusammenhang wird erst klar, wenn man sich die Pyramiden in den ganzen Raum ausgedehnt vorstellt und die Anordnung der Kugeln unter verschiedenen Perspektiven betrachtet. Ganz deutlich fällt das links in Bild 1 auf: Die Kugelebene, die die rechte Flanke der Pyramide bildet, ist offensichtlich eine dreieckige Anordnung wie in der rechten Grafik in Bild 2. Umgekehrt kann man von der ABCABC...-Schichtung (kubische Kugelpackung aus Aufgabe 8) ausgehen; in Bild 10 schauen wir ins Innere und finden quadratisch angeordnete Schichten (mit Punkten markiert):

Bild 10
Zusammenfassung
Für die Packungsdichte spielt es keine Rolle, ob man die einzelnen Ebenen der Kugeln in quadratischen oder dreieckigen Anordnungen auslegt. Bei den dreieckigen Anordnungen gibt es zwei Varianten (Kurzform ABABAB bzw. ABCABC), die auch in Mischformen vorkommen können. Die quadratische Anordnung ist identisch mit ABCABC .
Diese Packungsdichte beträgt 74,05 % ; sie wurde von Thomas Hales als die maximal mögliche Packungsdichte nachgewiesen.
Beim Pyramidenbau in Tetraeder-Form kommt nur die Schichtung ABCABC... vor.
|
Publiziert 2018-10-11 Stand 2018-01-13
voriges Problem | Liste aller Probleme mit Lösungen | nächstes Problem
Manfred Börgens |
zur Leitseite