Manfred Börgens
Mathematische Probleme     Jubiläumsseite  Stern # 100 Stern		 Liste aller Probleme mit Lösungen
voriges Problem      nächstes Problem		 zur Leitseite


Walmdach

          Die Lösung steht im unteren Teil der Seite.

Zum Jubiläum dieser Seite gibt es ein klassisches Extremwertproblem.

In Bild 1 sieht man ein Walmdach (blau), dessen typische 5-Balken-Konstruktion rechts zu sehen ist.

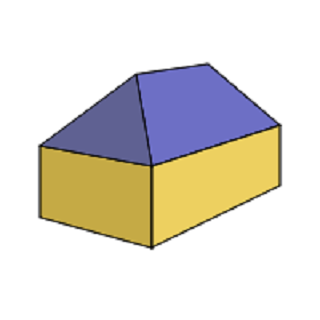
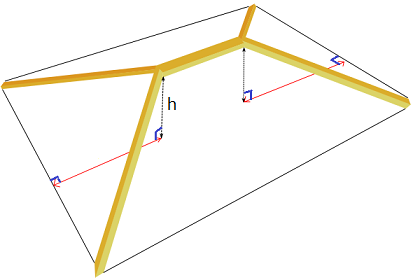
Walmdach 1                  Walmdach 2
Bild 1

Wir wollen hier nur vollständig symmetrische Walmdächer betrachten. Diese haben einen Firstbalken der Länge  x , der in beiden Dimensionen mittig zum Dach liegt, und vier Schrägbalken der Länge  s .

Drei Maße des Daches sind fest vorgegeben: Es ruht auf einem Rechteck mit den Seitenlängen  a  und  b , und seine Höhe (also die Höhe des Firstbalkens über dem Dachboden) ist  h .

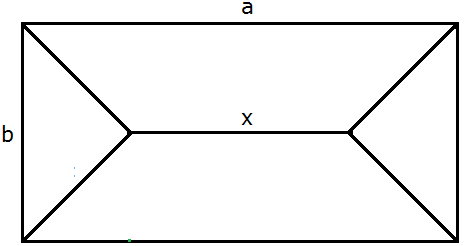
Draufsicht

Bild 2  -  Draufsicht

Aufgabe 1a
Wie ist  x  zu wählen, damit die Gesamtlänge aller fünf Balken minimal wird?
Aufgabe 1b
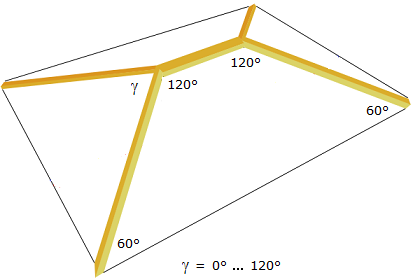
Wie lässt sich die Minimallösung mit Hilfe der Winkel zwischen den Balken ausdrücken?

Aufgabe 2
Wie ist  x  zu wählen, damit die Dachfläche minimal wird?

Lösung


Da die Längen  a  und  b  beliebig gewählt werden können, können wir zunächst ohne Einschränkung annehmen, dass der First parallel zur Seite mit der Länge  a  liegt, so wie in Bild 2.

Der maximale Definitionsbereich für unser Problem ist  x ∈[0,a]. Für ein echtes Walmdach ist  x ∈(0,a). Für  x = 0  liegt ein Spitzdach und für  x = a  ein Giebeldach vor.

Aufgabe 1a
Wie ist  x  zu wählen, damit die Gesamtlänge aller fünf Balken minimal wird?

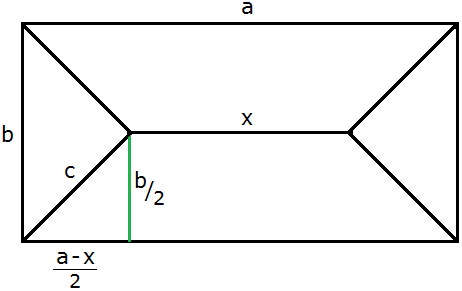
Draufsicht_Loesung

Bild 3 - Draufsicht

Man beachte, dass in Bild 2  c ≠ s  ist, da es sich um die Draufsicht handelt.

4c2 = b2 +(a-x)2   s2 = h2 + c2   ⇒  Gesamtlänge der Balken: ya(x) = x + 4s = x + 2(4h2 + b2 + (a-x)2)1/2

Zur Vereinfachung setzen wir  da = 4h2 + b2 . Die Indizierung von  y  und  d  mit  a  soll darauf hinweisen, dass der First parallel zur  a-Seite liegt (diese Einschränkung wird später noch aufgehoben).

Zu minimieren ist also die Funktion

ya(x) = x + 2((a-x)2 + da )1/2

ya'(x) = 1 - 2(a-x)·((a-x)2 + da )-1/2

ya''(x) = 2da·((a-x)2 + da )-3/2 > 0

Also wächst  ya'  streng monoton. Entweder hat also  ya'  genau eine Nullstelle auf (0,a) (dort liegt dann ein striktes absolutes Minimum von  ya  vor), oder  ya'  ist auf (0,a) positiv (denn  ya'(a) > 0 ;  ya  wächst dann streng monoton).

Nun bestimmen wir das Minimum.

ya'(x) = 0   ⇔  1 + da/(a-x)2 = 4   ⇔  a-x = (da/3)1/2   ⇔   x = a -(da/3)1/2

Eine Lösung für  x ∈(0,a) erhalten wir also nur, falls  da < 3a2. Ansonsten ist  ya  für das Spitzdach ( x = 0 ) kleiner als für jedes Walmdach.

Die minimale Balkenlänge beträgt für  xmin = a -(da/3)1/2 :

ya(xmin) = a + (3da)1/2

Falls das Walmdach kein Minimum hat, ist der Grenzwert (Spitzdach):

ya(0) = 2(a2 + da )1/2.

Man sieht, dass bei Vorliegen eines Minimums für das Walmdach eine Verkürzung oder Verlängerung von  a  eine entsprechende Veränderung von  xmin  erzeugt. Verlängert man z.B. die Hausseite  a  um  1 m , so wird auch die Firstlänge  xmin  um  1 m  größer, wenn die Gesamtbalkenlänge minimal sein soll; insbesondere bleiben die Querbalken gleich.

In Bild 4 sieht man die Graphen für  ya  für zwei verschiedene Hausmaße (Einheit: m ). Im linken Bild gibt es ein Walmdach mit einem absoluten Minimum für  ya . Im rechten Bild sind  b  und  h  so vergrößert worden, dass kein solches Minimum mehr existiert; hier liegt das Minimum am linken Intervallrand  x = 0  und steht nicht mehr für ein Walmdach, sondern für ein Spitzdach.

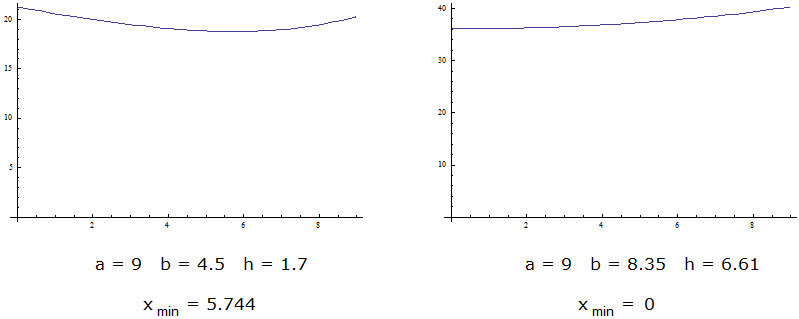
2 Skizzen
Bild 4


Warum ist das Problem damit nicht vollständig gelöst? Das liegt an unserer bisherigen Festlegung, dass der First parallel zur Hausseite mit der Länge  a  liegt. Dies führt dazu, dass für  a > b  der First immer parallel zur langen Hausseite und für  a < b  immer parallel zur kurzen Hausseite liegt. Der Bauherr könnte da aber eine Vorliebe haben: Er zieht vielleicht eine der beiden Varianten vor. Oder aber er stellt sich die Frage: Kann es vielleicht zwei Minima geben, wenn man einen First sowohl parallel zur langen oder zur kurzen Seite in Betracht zieht?

Um nun die Problemstellung in diesem allgemeineren Rahmen zu betrachten, wollen wir ab hier immer  a ≥ b  annehmen, aber je eine Funktion  ya  für den First parallel zur langen und  yb  für den First parallel zur kurzen Seite definieren. Dabei ergibt sich  yb  aus  ya (wie bereits definiert) durch Vertauschung von  a  und  b :

ya(x) = x + 2((a-x)2 + da )1/2

yb(x) = x + 2((b-x)2 + db )1/2    mit  x ∈[0,b]  und  db = 4h2 + a2.

Es kann tatsächlich zwei lokale Minima geben. Dazu muss (mit der gleichen Argumentation wie bei  ya)   db < 3b2  gelten. Für das Minimum erhalten wir:

xmin = b -(db/3)1/2
yb(xmin) = b + (3db)1/2

In Bild 5 sehen wir einen solchen Fall (in der Draufsicht). Die Hausmaße  a, b, h  sind unter der Graphik angegeben (Einheit: m ).   x  entspricht in beiden Bildern dem optimalen Wert, so dass die Gesamtbalkenlänge minimal wird.

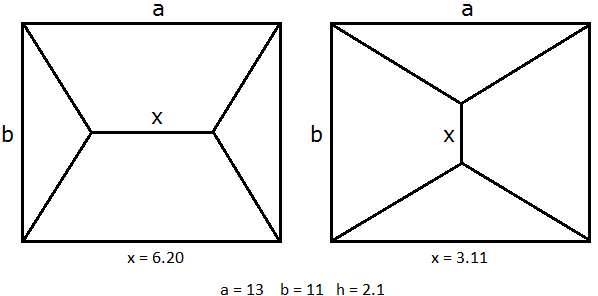
2 Minima
Bild 5

Aus  db < 3b2  folgt  da < 3a2 (aber nicht umgekehrt) wegen  a ≥ b , wie man leicht nachrechnet. Somit liegt für alle Walmdächer mit  a > b  einer von drei Fällen vor:

-  ya  und  yb  haben beide ein Minimum         ↔        db < 3b2
-  ya  hat ein Minimum, aber  yb  nicht            ↔        da < 3a2, db ≥ 3b2
-  ya  und  yb  haben beide kein Minimum        ↔        da ≥ 3a2

Die drei Fälle werden in Bild 6 illustriert. Dort steht die untere Kurve für  ya , die obere für  yb .

Man kann zeigen: Auf (0,b) ist  ya < yb .
Dies folgt aus  (a-x)2 + da < (b-x)2 + db  durch Ausmultiplizieren.

Also ist im Falle von zwei Minima das Minimum für  ya  das absolute (linke Graphik in Bild 6).

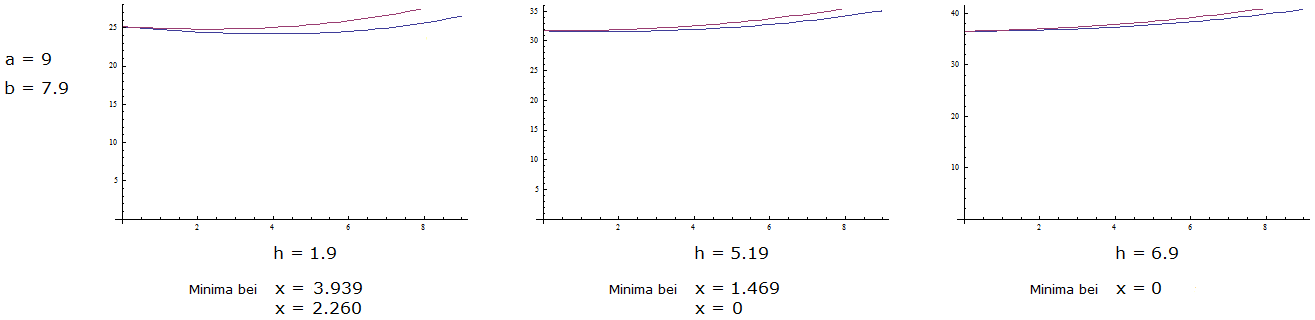
3 Doppelgraphen
Bild 6

In Bild 6 wurde die Grundfläche des Daches konstant gehalten, nur die Dachhöhe wurde variiert.

Nun sollen die bisherigen Ergebnisse zusammengefasst werden:

Auf einem Haus mit den Seitenlängen  a, b  und  a ≥ b  soll ein echtes Walmdach der Höhe  h  mit der Firstlänge  x  errichtet werden. Echt bedeutet:  x ∈(0,a), falls der First parallel zur langen Hausseite liegt, und  x ∈(0,b), falls er parallel zur kurzen Hausseite liegt.

1. Fall: Der Bauherr will den First parallel zur langen Seite liegen haben, oder es ist ihm gleichgültig, wie der First liegt.

Falls  4h2 + b2 < 3a2  →   Es gibt genau ein absolutes Minimum für die Gesamtbalkenlänge  y ; der First muss dafür parallel zur langen Hausseite liegen; das Minimum liegt bei
xmin = a -((4h2 + b2)/3)1/2
ymin = a + (12h2 + 3b2)1/2

Falls  4h2 + b2 ≥ 3a2  →   Es gibt kein Minimum für  y ; je kürzer der First, desto kürzer ist  y ; erst im Grenzwert  x → 0  (Spitzdach) würde das Minimum  2(a2 + b2 + 4h2 )1/2  für  y  erreicht.


2. Fall: Der Bauherr will den First parallel zur kurzen Seite liegen haben.

Falls  4h2 + a2 < 3b2   →   Es gibt genau ein absolutes Minimum für die Gesamtbalkenlänge  y ; es liegt bei
xmin = b -((4h2 + a2)/3)1/2
ymin = b + (12h2 + 3a2)1/2

Falls  4h2 + a2 ≥ 3b2  →   Es gibt kein Minimum für  y ; je kürzer der First, desto kürzer ist  y ; erst im Grenzwert  x → 0  (Spitzdach) würde das Minimum  2(a2 + b2 + 4h2 )1/2  für  y  erreicht.


Aufgabe 1b
Wie lässt sich die Minimallösung mit Hilfe der Winkel zwischen den Balken ausdrücken?

In Bild 7 wollen wir zwei Winkel bestimmen:  BAD  und  BAC .

Winkel

Bild 7

In Bild 7 legen wir den Koordinatenursprung in  R3  nach  C :
A=((a-xmin)/2, b/2, h)
B=(0, b, 0)
C=(0, 0, 0)
D=((a+xmin)/2, b/2, h)

Für die Winkelberechnung benötigt man die Vektoren
AB = B - A
AC = C - A
AD = D - A

Der Winkel  BAD  ist dann gleich  arccos( AB·AD /(||AB||·||AD||)) (das erste Produkt ist ein Skalarprodukt; die Norm  ||·||  steht für die euklidische Vektorlänge). Eine kurze Rechnung zeigt:

Winkel BAD = 120°

Charakteristisch für die Minimallösung ist also, dass die beiden viereckigen (trapezförmigen) Dachseiten die Winkel  120°-120°-60°-60°  aufweisen, siehe Bild 8.

Für den Winkel  γ = BAC  berechnet man:
AB·AC = - b2/6 + 4h2/3     ||AB||·||AC|| = b2/3 + 4h2/3

γ → 120°  für  h → 0 .
γ → 0°  für  h → +∞ .

Winkel

Bild 8  Optimallösung


Aufgabe 2
Wie ist  x  zu wählen, damit die Dachfläche minimal wird?

Wir übernehmen aus Aufgabe 1 die Bezeichnungen, die zur Definition von  ya  benötigt wurden. Die Dachfläche besteht aus zwei Dreiecken und zwei Trapezen. Die Dreiecke haben die Basis  b  und die Höhe  ((a-x)2/4 + h2)1/2 . Die Trapeze haben die Mittellänge  (a+x)/2  und die Höhe  (b2/4 + h2)1/2 . Als Flächeninhalt  F  des Daches erhalten wir also:

F(x) = b·((a-x)2/4 + h2)1/2 + (a+x)·(b2/4 + h2)1/2

F'(x) = (-b/2)·(a-x)·((a-x)2 + 4h2)-1/2 + (b2/4 + h2)1/2 =
      = (1/2)·((a-x)2 + 4h2)-1/2·(-b(a-x) + ((b2 + 4h2)((a-x)2 + 4h2))1/2) > 0
                    ↓          ↓         ↓
                   > 0             - Y            + Z

Dass  F' positiv ist, sieht man so: Die Ableitung wurde so umgeformt, dass der Vorfaktor (bis zur großen Klammer) positiv ist. Der erste Summand  -Y  in den großen Klammern ist negativ, der zweite Summand  Z (der gesamte Wurzelausdruck) positiv. Durch Ausmultiplizieren von  Z  erkennt man  Y2 < Z2 , somit auch  Y < Z . Daraus folgt, dass  F' positiv ist.  F  hat also auf dem Definitionsbereich (0,a) kein Extremum, sondern wächst streng monoton.

Zum gleichen Ergebnis gelangt man in analoger Weise (durch Vertauschung von  a  und  b ), wenn der First parallel zur Hausseite mit der Länge  b  liegt.

Die Dachfläche von Walmdächern weist kein Minimum auf. Ein Minimum würde man für den Grenzwert  x → 0  erhalten, also für ein Spitzdach. Dessen Dachfläche beträgt  (a√da + b√db)/2 .


Publiziert 2017-10-18          Stand 2015-08-28

voriges Problem   |   Liste aller Probleme mit Lösungen   |    nächstes Problem

Manfred Börgens   |    zur Leitseite