... tun manche von ihnen aber doch - jedenfalls in der folgenden Geschichte. Die habe ich mir nicht ausgedacht, sondern sie stammt aus einer Zeitschrift, also nehme ich auch keine Beschwerden von gekränkten Pfadfindern an. In der Zeitschrift wurde die Geschichte als "Rätsel" angekündigt, die "Lösung" fand sich passenderweise in der gleichen Ausgabe. Der Name der Zeitschrift wird hier mildherzig verschwiegen, denn das Rätsel und die angegebene Lösung sind barer Unsinn. Aber dadurch wird die Sache erst interessant und verlangt nach einer genaueren Untersuchung.
Hier kommt das "Rätsel":
In einer großen Runde am Lagerfeuer sitzen Pfadfinder. Einige sind notorische Lügner, die anderen sagen immer die Wahrheit. Jeder sagt, seine beiden Sitznachbarn seien Lügner. Ein Junge sagt "Wie witzig, wir sind genau 99 Pfadfinder hier am Feuer". Darauf antwortet einer seiner Nachbarn: "Du lügst, wir sind genau 100 ." Wieviele Pfadfinder saßen am Feuer?
Aua.
Hier kommt die "Lösung":
Neben jedem Lügner müssen zwei sitzen, die die Wahrheit sagen, sonst könnte nicht jeder seine Nachbarn Lügner nennen. Deshalb muss die Zahl gerade sein. 100 ist also richtig.
Nochmal aua.
Erstens
Was ist falsch an der Lösung? Was bedeutet das für die Lösbarkeit des Rätsels?
Zweitens
Sei n die Anzahl der Pfadfinder. Da jeder zwei Nachbarn haben soll, ist n ≥ 3 . Machen Sie eine kleine Tabelle, in der für n = 3,...,10 die Anzahl der möglichen Sitzordnungen der Pfadfinder eingetragen wird. In Bild 1 sieht man alle vier möglichen Sitzordnungen für n = 8 . Weiße Kreise stehen für wahrheitsliebende Pfadfinder, schwarze für Lügner. Für die Zählung wird folgendes vereinbart: Man fixiert einen der Wahrheitsliebenden (grüner Pfeil in Bild 1) und zählt dann alle unterschiedlichen Anordnungen aus seiner Sicht.
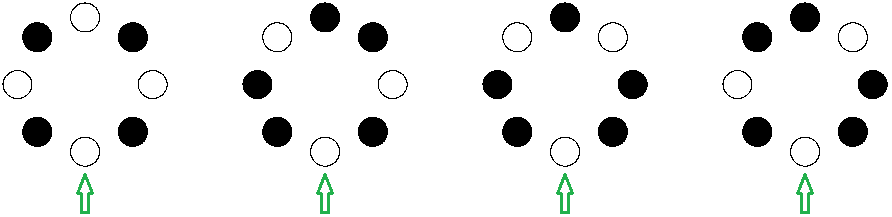
Bild 1
Drittens
Für die Identifikation von Folgen ganzer Zahlen gibt es die ausgezeichnete Datenbank OEIS. Geben Sie die Anzahlen für die möglichen Sitzordnungen für n = 3,...,10 dort ein. OEIS gibt Ihnen den Namen der Folge, weitere Folgenglieder und eine Rekursionsformel an. Beachten Sie, dass es verschiedene Möglichkeiten gibt, bei welchem Glied man die Folge beginnen lässt. Bei unserer Aufgabenstellung wird die Folge (an)n≥3 gebildet, also z.B. a8 = 4 (Bild 1). Überzeugen Sie sich, dass die Rekursionsformel für die von Ihnen gefundenen Folgenglieder stimmt.
Viertens
Die Rekursionsformel für die Folge aus OEIS muss man nicht einfach glauben. Es sollte überprüft werden, ob sie für beliebige n auf unser Pfadfinder-Problem anwendbar ist. Dazu ist es hilfreich, die Sitzordnung zu codieren. Ausgehend von der fixen Position (grüner Pfeil in Bild 1) notiert man die Sitzordnung im Uhrzeigersinn. Man erkennt, dass es nur Zweiergruppen (weiß-schwarz) und Dreiergruppen (weiß-schwarz-schwarz) gibt. Für das Beispiel n = 8 (Bild 1) ist die Abfolge bei den vier Möglichkeiten:
2 2 2 2
3 3 2
3 2 3
2 3 3
Die Summe dieser Zahlen muss zeilenweise natürlich wieder n = 8 ergeben. Das bedeutet allgemein, dass hier die natürlichen Zahlen n in geordnete Summanden 2 und 3 zerlegt werden. Aus dieser Überlegung ergibt sich dann der Beweisansatz für die Richtigkeit der Rekursionsformel.
Fünftens
Nun soll noch eine geschlossene Formel für die an gefunden werden. OEIS hat uns ja den Namen der Folge genannt. Wenn man diesen in der deutschen Wikipedia recherchiert, findet man eine Summenformel mit Binomialkoeffizienten. Auch hier (wie schon in OEIS) muss man auf die Nummerierung der Folge aufpassen, da aus der Rekursionsregel nicht hervorgeht, an welcher Stelle die Folge beginnen soll.
Zeigen Sie, dass diese Formel für die an der Rekursionsformel genügt.
Tipp: Das geht über die Summenformel für benachbarte Binomialkoeffizienten im Pascal'schen Dreieck; aber vorher muss man eine Indexverschiebung durchführen.
Sechstens
Suchen Sie die Binomialkoeffizienten aus der Summenformel im Pascal'schen Dreieck auf. Sie bilden ein interessantes Muster.
Siebtens
Ganz am Anfang stand ein Rätsel aus einer Zeitschrift. Was lässt sich nun dazu sagen?
Lösung