Aufsteigende Würfel 2                     Problem # 97 :  Aufsteigende Würfel 1

          Die Lösung steht im unteren Teil der Seite.




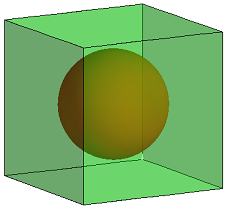
Bild 1


Für das Spiel in Problem # 97 werden sechs Würfel mit aufsteigender Größe benötigt. Damit alle das gleiche Gewicht haben, soll nur der kleinste massiv sein; die anderen sind innen ausgehöhlt. Das soll nun genauer definiert werden:

(a)  Die Würfel sind alle aus dem gleichen homogenen Material gefertigt.

(b)  Ihre Kantenlänge wächst von einem Würfel zum nächstgrößeren mit einem festen Faktor  q > 1 . Der kleinste Würfel soll die Kantenlänge  1  haben.

(c)  Der kleinste Würfel ist massiv. Alle anderen sind innen kugelförmig ausgehöhlt. Die inneren Hohlkugeln haben ihren Mittelpunkt im Mittelpunkt der Würfel (siehe Bild 1). Ihr Durchmesser ist maximal so groß wie die Kantenlänge des zugehörigen Würfels.

(d)  Alle (Hohl-)Würfel haben das gleiche Gewicht wie der massive (kleinste) Würfel.

Nun zur Aufgabe:

Geht das mit allen  q > 1 ?  Falls nicht: Welche  q  sind mit (a) - (d) vereinbar?

Ein bestimmtes  q  sei festgelegt. Welche Radien haben dann die Hohlkugeln im Inneren der Würfel?  Betrachten Sie auch den Spezialfall, dass die Hohlkugel an die Seiten des Würfels stößt.

Lösung

Wir wählen die folgenden Bezeichnungen (für  i = 1 ... 6 ) :

V_i  Volumen der Würfel (massiver Würfel mit Volumen  V₁ , Hohlwürfel nach Kantenlänge aufsteigend geordnet mit Volumen  V₂ ... V₆ ).

r_i  Radien der Innenkugeln ( r₁ = 0  für den kleinsten Würfel; für  i = 2 ... 6  gehört  r_i  zum Hohlwürfel mit Volumen  V_i ).

Dann gilt:

Volumen der Vollwürfel (ohne Hohlraum):  V_i^voll = (q^i-1)³

Volumen der Hohlkugeln:  V_i^Kugel = ⁴/₃·π·r_i³

Da alle  V_i = 1  sind, folgt

(1)  V_i = V_i^voll - V_i^Kugel = (q^i-1)³ - ⁴/₃·π·r_i³ = 1

Wir lösen nach  r_i  auf, um die zweite Frage aus der Aufgabenstellung zu beantworten:

(2)  r_i = (^.75/_π(q^3(i-1)-1))^1/3

Nun gibt es aber eine Einschränkung: Wegen (c) muss  r_i ≤ q^i-1/2  gelten. Ist das mit (2) vereinbar? Aus der Ungleichung und (2) folgt:

(3)  q^3(i-1) = 1 + ⁴/₃·π·r_i³ ≤ 1 + ^π/₆·q^3(i-1)

(4)  q^3(i-1) ≤ 1/(1-π/6)

(5)  i = 6 :  q ≤ q_max = (1-π/6)^-1/15 ≈ 1.050675

Es gilt auch die Umkehrung der Argumentation, die zu (5) führte, d.h. aus (5) folgt  r_i ≤ q^i-1/2 . Denn aus (5) folgt (4) wegen  q^3(i-1) ≤ q¹⁵ ≤ 1/(1-π/6) . -  q^3(i-1) ≤ 1/(1-π/6)  ist aber gleichbedeutend mit  q^3(i-1) ≤ 1 + ^π/₆·q^3(i-1) , also gilt auch die Ungleichung in (3), die wiederum äquivalent zu  r_i ≤ q^i-1/2  ist.

Wir fassen zusammen:

Alle Hohlkugeln "passen" in die Würfel    ⇔  r_i ≤ q^i-1/2  ⇔  q ≤ (1-π/6)^-1/15

Damit ist auch die erste Frage aus der Aufgabenstellung beantwortet. Es ergibt sich nur ein sehr kleiner Spielraum für den Faktor  q , nämlich zwischen  1  und ca.  1.05 .

Woran liegt das? Ein "Restkörper" (ein Würfel mit Kantenlänge  a  ohne Innenkugel) hat mindestens das Volumen  V(a) = a³ - ⁴/₃·π·(a/2)³  (also Würfelvolumen abzüglich der maximal großen Kugel).  V(a) = a³(1 - ^π/₆) ;  für  a → +∞  gilt  V(a) → +∞ , somit muss  a  nach oben beschränkt bleiben, wenn  V = 1  sein soll; bei maximal großer Innenkugel ist  a = (1 - ^π/₆)^-1/3 . Das entspricht den oben hergeleiteten Ergebnissen mit  a = q⁵_max  (größter Würfel mit maximaler Innenkugel; siehe Bild 2, die Berührungspunkte von Kugel und Würfel sind weiß markiert).



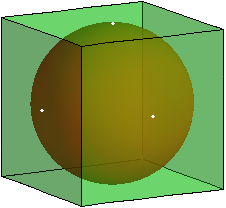
Bild 2

Damit ist gezeigt, dass für  q = q_max  die Hohlkugel des 6. Würfels an die Seiten des Würfels stößt. Der Vollständigkeit halber wollen wir noch etwas ausführlicher darlegen, dass dies nur beim größten Würfel auftreten kann.

Das Verhältnis  r_i/q^i-1 (Radius Innenkugel / Kantenlänge Würfel) wächst streng monoton sowohl mit  i  als auch mit  q :

(r_i/q^i-1)³ = 3(1-q^-3(i-1))/(4π)

Der maximale Wert wird also für  i = 6  und  q = q_max  angenommen:  r₆/q⁵_max = 1/2

Nur beim 6. Würfel und nur für  q = q_max  ist der Durchmesser der Innenkugel gleich der Kantenlänge des Würfels (Bild 2).

Publiziert 2017-04-08          Stand 2015-12-31

voriges Problem   |   Liste aller Probleme mit Lösungen   |    nächstes Problem