Schattenwurf


Dies ist nach  Problem # 54  die zweite Aufgabe zur Schattenlänge.


Ein Mann lebt in den mittleren nördlichen Breiten, also zwischen dem nördlichen Wendekreis (der z.B. etwas südlich des Assuan-Staudamms des Nils in Ägypten verläuft) und dem nördlichen Polarkreis (der durch Lappland verläuft).

Sein Schatten ist am Mittag eines bestimmten Tages  1,35 m  lang. Viele Wochen später misst der Mann seinen Schatten erneut (mittags am selben Standort) und kommt auf  13,9 m .

Aufgabe 1    Auf welchen Breitengraden könnte der Mann leben?

Aufgabe 2    Einer der möglichen Breitengrade aus Aufgabe 1 ist  60°. Auf diesem Breitengrad möge der Mann wohnen. Welche Körpergröße könnte er haben?

Aufgabe 3    Eine der möglichen Körpergrößen aus Aufgabe 2 ist  1,80 m . Diese Größe möge der Mann haben. An welchen Tagen hat er seinen Schatten gemessen?

Damit die Aufgabe nicht zu schwer wird, gehen wir von der idealisierten Annahme aus, dass die Erde kugelförmig ist.  -  Für die Lösung ist der Zusammenhang zwischen Sonnenstand und Datum wichtig. Tabellen dazu findet man durch eine Recherche zum Stichwort Deklination.

Lösung

Zunächst muss wohl geklärt werden, wie die Schattenlänge  a  vom Breitengrad  φ (Frage 1), von der Körpergröße  h (Frage 2) und von der Jahreszeit (Frage 3) abhängt. Eine Skizze (Bild 1) soll bei der Antwort helfen.



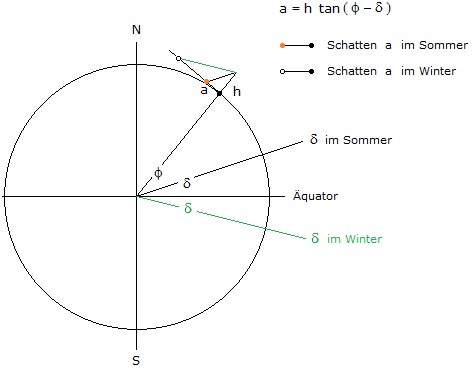
Bild 1


In Bild 1 ist die entscheidende Formel schon angegeben:  a = h·tan(φ-δ) . Die Skizze zeigt den Querschnitt durch den Globus, der durch die Pole und den Standpunkt des Beobachters (schwarzer Punkt) auf dem Breitengrad  φ  verläuft. Der Beobachter (seines eigenen Schattens) hat die Höhe  h  (natürlich sind  h  und der Schatten  a  in der Skizze stark überzeichnet worden). Die Problemstellung legt die Messung des Schattens auf die Mittagszeit fest, also beim täglichen Sonnenhöchststand. Wir können uns also die Sonne in der Querschnittebene der Skizze denken, und zwar weit rechts im Bild. Nun kommt die Deklination  δ  ins Spiel. Dies ist der Winkel relativ zur Äquatorebene, unter dem die Sonnenstrahlen die Erde treffen. Im Sommerhalbjahr ist  δ  positiv (d.h. die Sonne steht nördlich vom Äquator), im Winterhalbjahr negativ, und zu Frühlings- und Herbstanfang ist  δ = 0 , dann steht die Sonne in der Äquatorebene.

Wie betrachten nun das rechtwinklige Dreieck mit  h  und  a  als Katheten (doppelt eingezeichnet für Sommer und Winter). Der Winkel an der rechten Ecke (quasi beim Kopf des Mannes) ist  φ-δ , da die Hypothenuse von dieser Ecke zum Ende des Schattens (orangener bzw. weißer Punkt in der Skizze) parallel zu der eingezeichneten  δ-Linie liegt. Somit ist  tan(φ-δ) = a/h .

Welche Werte können für  φ  und  δ  eingesetzt werden? Es gilt  δ ∈ (-23,44°, 23,44°)  und nach Aufgabenstellung  φ ∈ (23,44°, 66,56°) .

Aufgabe 1
Auf welchen Breitengraden könnte der Mann leben?

Wegen  φ-δ ∈(0°, 90°) kann  tan(φ-δ) und damit die Schattenlänge  a  alle positiven reellen Werte annehmen. Sehr kleine Schattenlängen würden wir am Sommeranfang (δ = 23,44°) in der Nähe des nördlichen Wendekreises (also  φ ≈ 23,44°) messen. Beliebig große Schattenlängen kommen am Winteranfang (δ = -23,44°) in der Nähe des nördlichen Polarkreises (also  φ ≈ 66,56°) vor.

Könnte der Mann mitten in Deutschland leben, also z.B. auf  50° nördlicher Breite? Wir kennen nur zwei Schattenlängen. Ihr Verhältnis beträgt  a₁/a₂ = 13,9/1,35 ≈ 10,3 . Ein so großes Verhältnis zweier Schattenlängen kommt in Deutschland nicht vor. Um das zu verstehen, zeichnet man (Bild 2) zunächst die Graphen für  a/h = tan(φ + 23,44°) (obere Kurve) und  a/h = tan(φ - 23,44°) (untere Kurve). Diese beiden Funktionen beschreiben das Verhältnis von Körpergröße und Schattenlänge zu den beiden Extremzeitpunkten, also zu Winter- und Sommeranfang (siehe Bild 2).


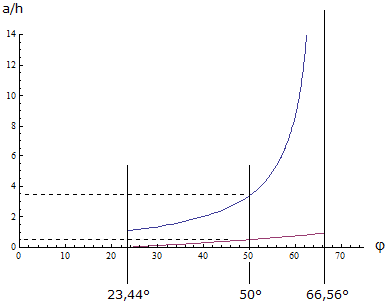
Bild 2

In Bild 2 sieht man auch die Verhältnisse in Deutschland (φ = 50°). Die gestrichelten Linien zeigen an, dass  a/h  zwischen ca.  0,5  und  3,363  liegt. Das kann man übersetzen in das Verhältnis zweier beobachtbarer Schattenlängen  a₁/a₂ , das dann für  φ = 50°  maximal ca.  3,363/0,5 ≈ 6,73  beträgt. Auch ganz im Norden von Deutschland (φ = 55°) und im äußersten Süden (φ = 47,25°) sind die Verhältnisse ähnlich.

Wir müssen also nur die Quotienten der Kurvenwerte aus Bild 2 berechnen, d.h.  tan(φ + 23,44°)/tan(φ - 23,44°), um festzustellen, wo  a₁/a₂  den Wert  13,9/1,35 ≈ 10,3  aus der Aufgabenstellung annehmen kann. Das Ergebnis ist in Bild 3 zu sehen.


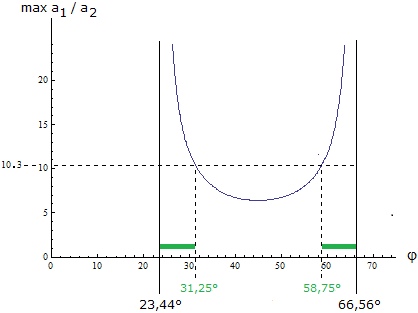
Bild 3

Auf den grün eingezeichneten Breitengraden in Bild 3 liegen z.B. Alexandria in Ägypten bzw. Norrköping in Schweden. An diesen Orten könnte man also ein Verhältnis der Schattenlängen wie in der Aufgabenstellung feststellen, und zwar wenn man genau zu Winter- und Sommeranfang misst. Auf den Breiten zwischen dem nördlichen Wendekreis und Alexandria sowie auf den Breiten zwischen Norrköping und dem nördlichen Polarkreis (grüne Balken) könnte man sogar noch extremere Verhältniswerte erhalten. Die grünen Balken in Bild 3 markieren also die Breitengrade, auf denen der Mann aus der Aufgabenstellung leben könnte.

Nun sieht es so aus, als ob man die Lösung der Aufgabe 1 aus der Grafik abgelesen hätte (was ja auch zumindest näherungsweie möglich und als Lösung akzeptabel wäre). Es gibt aber auch die folgende analytische Lösung. Wir setzen zunächst:

A = a₁/a₂ , a₁ > a₂
γ = 23,44°
c = tan γ

Gesucht sind Lösungen  φ  von
(1)   tan(φ+γ)/tan(φ-γ) = A

Additionstheorem für den Tangens:
tan(φ±γ) = (tan φ ± tan γ)/(1 ∓ tan φ tan γ)

(1) wird also mit  t = tan φ  zur quadratischen Gleichung
(t+c)(1+ct) = A(t-c)(1-ct)

Diese Gleichung formen wir um zu:
(2)   t² - t·(c + 1/c)(A-1)/(A+1) + 1 = 0

Damit können wir Aufgabe 1 (und andere Aufgaben mit beliebigen  A) exakt lösen. Wir setzen  A = 13,9/1,35  und erhalten die beiden Lösungen  t ≈ 0,60674  und  t ≈ 1,64816 . Mit  φ = arctan t  sind  φ ≈ 31,247°  und  φ ≈ 58,753° (vgl. Bild 3).

Der Mann aus der Aufgabenstellung könnte nördlich des Breitengrades  58,753° (der durch Norrköping in Schweden verläuft) bis zum nördlichen Polarkreis leben, oder südlich des Breitengrades  31,247° (der durch Alexandria in Ägypten verläuft) bis zum nördlichen Wendekreis.

Wenn  A  genügend klein wird, hat (2) nur eine Lösung (dann verläuft in Bild 3 die waagerechte gestrichelte Linie durch das Kurvenminimum) oder gar keine Lösung. Wir wollen untersuchen, wann das der Fall ist.

Mit  d = (c + 1/c)(A-1)/(A+1)  erhält man als "kritischen Punkt" für die Lösung von (2), also von  t² - t·d + 1 = 0 :

A₀ = (1/2 - c/(c²+1))^-1 - 1 ≈ 6,405315 .  Das bedeutet (vgl. Bild 3):

d > 2  ⇔  A > A₀    →    2 Lösungen
d = 2  ⇔  A = A₀    →    1 Lösung
d < 2  ⇔  A < A₀    →    keine Lösung

Damit haben wir die Aufgabe 1 allgemein, d.h. für beliebige Schattenlängen  a₁ > a₂  gelöst. Das soll nochmal übersichtlich dargestellt werden:

A > A₀   →   aus (2) erhält man zwei Winkel  φ₁ < φ₂ 
Im Intervall zwischen diesen beiden Winkeln liegen die Breitengrade, in denen die Schattenlängen nicht gemessen worden sein können; alle anderen Breitengrade (grüne Balken in Bild 3) kommen als Lösung in Frage. Eine Besonderheit liegt vor, wenn man sich genau auf  φ₁  oder  φ₂  befindet: dann ist das Verhältnis der beiden Schattenlängen bereits das maximal mögliche, so dass die Messungen nur zu Winter- und Sommeranfang durchgeführt worden sein können.

A = A₀   →   aus (2) erhält man genau einen Winkel  φ
Alle Breitengrade kommen als Lösung in Frage. Eine Besonderheit liegt vor, wenn man sich genau auf  φ  befindet: dann ist das Verhältnis der beiden Schattenlängen bereits das maximal mögliche, so dass die Messungen nur zu Winter- und Sommeranfang durchgeführt worden sein können.

A < A₀   →   (2) hat keine Lösung
Alle Breitengrade kommen als Lösung in Frage.


Aufgabe 2
Einer der möglichen Breitengrade aus Aufgabe 1 ist  60° . Auf diesem Breitengrad möge der Mann wohnen. Welche Körpergröße könnte er haben?

Nun kennen wir  a₁, a₂  und  φ . Die Gleichung  a₁ = h tan(φ-δ) (siehe Bild 1) hat genau eine Lösung  h  für jedes  δ ∈(-γ,γ). Die Gleichung hat also die Lösungsmenge

h ∈(a₁/tan(φ+γ), a₁/tan(φ-γ))

Analog erhält man für die Gleichung  a₂ = h tan(φ-δ) die Lösungsmenge

h ∈(a₂/tan(φ+γ), a₂/tan(φ-γ))

Da beide Gleichungen erfüllt sein müssen, liegt  h  in der Schnittmenge der beiden Lösungsmengen:

(3)   h ∈(a₁/tan(φ+γ), a₂/tan(φ-γ))

Wir überzeugen uns, dass diese Menge nicht leer ist:
φ  liegt im "grünen Bereich" in Bild 3, d.h.  A = a₁/a₂  liegt unterhalb der Kurve  tan(φ+γ)/tan(φ-γ) . Daraus folgt  a₁/tan(φ+γ) ≤ a₂/tan(φ-γ) .

Für  φ = 60°  erhalten wir mit (3) die Lösung zu Aufgabe 2: Der Mann ist mindestens  1,60 m  und höchstens  1,82 m  groß.


Aufgabe 3
Eine der möglichen Körpergrößen aus Aufgabe 2 ist  1,80 m . Diese Größe möge der Mann haben. An welchen Tagen hat er seinen Schatten gemessen?

Nun sind in unserer Grundgleichung  a = h tan(φ-δ) alle Werte außer  δ  bekannt. Wir lösen die Gleichung nach  δ  auf:

(4)   δ = φ - arctan(a/h);  hier:  δ = 60° - arctan(a/1,8)

Als der Mann seinen kurzen Schatten misst (a = 1,35), ist  δ ≈ 23,1301° .
Als der Mann seinen langen Schatten misst (a = 13,9), ist  δ ≈ -22,6215° .

Ein Blick in eine Deklinationstabelle zeigt, dass der kurze Schatten am 12.6. oder am 1.7. gemessen wurde, der lange Schatten am 8.12. oder am 6.1.
(Man beachte, dass in dieser Tabelle statt der Nachkommastellen die Minuten angegeben werden; Umrechnung: Minuten/60 ergeben Nachkommastellen; es gibt aber auch Deklinationstabellen mit Nachkommastellen.)


Zusammenfassung der allgemeinen Lösung

In der Aufgabenstellung könnten zwei beliebige Schattenlängen  a₁ > a₂  stehen. Um die erlaubten Breitengrade zu ermitteln, löst man Gleichung (2). Welche Breitengrade in Frage kommen, steht am Ende der Lösung zu Aufgabe 1.

Kennt man zusätzlich den Breitengrad des Beobachters, so gibt (3) die möglichen Körpergrößen an.

Kennt man außerdem die Körpergröße, so gibt (4) die Deklinationen der Sonne und damit die zum Problem passenden Daten an.



Kategorie: Geomathematik

Publiziert 2015-06-26          Stand 2014-07-14

voriges Problem   |   Liste aller Probleme mit Lösungen   |    nächstes Problem