101
Die Lösung steht im unteren Teil der Seite.
101 ist ein objektives (oder neutrales) 2-Personen-Spiel, das auch Unentschieden zulässt ( → Spieltheorie).
"Spielbrett": n nebeneinander angeordnete (zunächst leere) Felder; n ≥ 3 (im Bild n = 9 ).

Spielregel: Die Spieler A (Anziehender) und B (Nachziehender) füllen abwechselnd die Felder in beliebiger Reihenfolge aus; es sind nur die Einträge 0 oder 1 erlaubt. Der Spieler, der als erster die Teilfolge ...101... erzeugt, ist Sieger.
Da es sich um ein endliches objektives Spiel handelt, muss es optimale Strategien für A bzw. B geben. Diese wollen wir suchen. Wir werden sehen, dass diese Strategien von n abhängen.
An dieser Stelle könnte die Problemstellung enden. Wer also ohne weitere Hilfe die Lösung finden möchte, soll einfach nicht weiterlesen.
Für dieses Problem gibt es einen Schlüssel, der sehr einfach zu formulieren, aber nicht leicht zu finden ist. Wenn man geduldig ausprobiert, welche Spielsituation (immer!) beim letzten Zug vor dem Gewinnzug vorliegt, kann man den Schlüssel finden.
Für die Ungeduldigen soll der Schlüssel hier offenbart werden. Interessant wird dann der zweite Teil des Problems: Wie sollen A und B den Schlüssel für ihre Strategie verwerten?
Schlüssel: Ein Spieler kann nur gewinnen, wenn der Gegner gezwungen ist, in der folgenden Konstellation eines der leeren Felder zwischen den Einsen auszufüllen.

Noch ein Hinweis: A oder B werden versuchen, die Schlüssel-Konstellation bei Spielbeginn so schnell wie möglich zu erzeugen. Probieren Sie dies am besten zuerst für große n aus.
Lösung
Im Original wurde dieses Spiel mit Y2K Game bezeichnet, und statt 101 wurde SOS verwendet (Mathematics Magazine 73/3).
Der Spieler, der nur noch zwei leere Felder zwischen zwei Einsen vorfindet, hat offenbar verloren. Das gilt auch, wenn es mehrere solcher Lücken gibt, aber sonst alles ausgefüllt ist, wie z.B. in dem folgenden Bild:
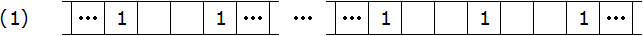
Es soll bewiesen werden, dass keine anderen Konstellationen zum Erfolg führen können. Wir betrachten den vorletzten Zug (also den des Verlierers). Dieser Zug muss sowohl beim Eintrag einer 1 als auch einer 0 zum Verlust führen. Da bei beiden Spielern optimales Spiel vorausgesetzt wird, kann es in allen früheren Zügen keine Gelegenheit gegeben haben, die 101 zu erzeugen. Der Eintrag einer 1 oder einer 0 beim vorletzten Zug muss also in eines der drei Felder der (im nächsten Zug siegbringenden) 101 erfolgen, ein weiteres (passendes) muss bereits ausgefüllt sein, und das dritte muss noch leer sein (für den Gewinnzug). Wir gehen beide Möglichkeiten durch (vorletzter Zug ins grüne Feld):
1. Fall: Der vorletzte Zug ist eine 0. Damit dieser Zug dem anderen Spieler zum Gewinn verhilft, muss ein Nachbarfeld eine 1 enthalten und das andere leer sein.

2. Fall: Der vorletzte Zug ist eine 1. Nur wenn angrenzend an das leere Feld eine 1 steht, kann der andere Spieler im nächsten Zug gewinnen.

Also muss vor dem vorletzten Zug die Konstellation (1) vorgelegen haben.
Die folgende Strategie liegt also nahe: Man setzt (möglichst früh im Spiel) eine 1, und wenn man das nächste Mal am Zug ist, setzt man eine weitere 1 drei Felder daneben (das ist natürlich nur dann erfolgversprechend, wenn am Ende des Spiels der Gegner den vorletzten Zug machen muss):
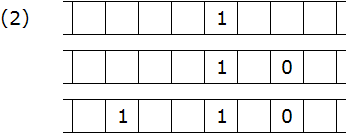
Die 0 in der zweiten Zeile steht für den Versuch, die Schlüsselkonstellation zu verhindern. - Das Spiel geht nun weiter, bis die Konstellation (1) übrigbleibt. Dort gibt es eine gerade Anzahl leerer Felder. Wer am Zug ist, verliert. Das führt uns zu einem ersten Teilergebnis:
- A kann nur gewinnen, falls n ungerade ist.
- B kann nur gewinnen, falls n gerade ist.
Insbesondere ist es für den Ausgang des Spiels gleichgültig, welcher der beiden Spieler eine Schlüsselkonstellation herstellt. Wenn z.B. n ungerade ist und A so wie in (2) vorgeht, nützt es B nichts, danach das Gleiche zu tun. Auf der anderen Seite schadet es A bei geradem n , so wie in (2) zu handeln.
Wir werden sehen, dass n genügend groß sein muss, um einen Gewinn zu ermöglichen (für sehr kleine n sieht man sofort, dass das Spiel unentschieden ausgeht).
Wie groß muss das Spielfeld sein, damit A mittels (2) gewinnt? Da B immer eine Seite der zuerst gesetzten 1 blockieren kann, müssen auf jeder Seite dieser 1 drei freie Felder sein. Das bedeutet:
- A gewinnt genau dann, wenn n ≥ 7 und ungerade ist.
B macht es ähnlich, benötigt aber mehr Platz, da A mit seinem ersten Zug (A1) die Mitte versperren kann (Position n/2 oder n/2 + 1 ; im ersten Fall spielt B rechts weiter, sonst links):

B muss also mit seinem ersten Zug (B1) sowohl von der Mitte als auch vom Rand genügend weit weg bleiben, um (3) (evtl. spiegelbildlich) erzeugen zu können. A's zweiter Zug (A2) steht wieder nur symbolisch für eine Blockade der Schlüsselkonstellation und könnte auch links von B1 erfolgen.
n = 14 ist offenbar noch nicht groß genug dafür (obwohl bei B's erstem Zug 7 benachbarte Leerfelder zur Verfügung stehen):

A macht erst die Mitte dicht, versperrt dann das rechte Ende. Jetzt müsste B Feld 8 mit einer 1 besetzen, um die Schlüsselkonstellation zu erzeugen. Aber dann verliert B, weil A mit einer 1 auf Feld 6 gewinnt.
Fazit:
- B gewinnt genau dann, wenn n ≥ 16 und gerade ist.
Es folgt eine Übersicht für 3 ≤ n ≤ 23 .  steht für Sieg von A,
steht für Sieg von A,  für Sieg von B und
für Sieg von B und  für Unentschieden.
für Unentschieden.

Publiziert 2011-09-27 Stand 2010-12-31
voriges Problem | Liste aller Probleme mit Lösungen | nächstes Problem
Manfred Börgens |
zur Leitseite


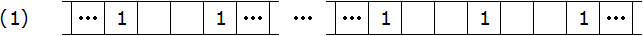





 steht für Sieg von A,
steht für Sieg von A,  für Sieg von B und
für Sieg von B und  für Unentschieden.
für Unentschieden.
