Warum ist  1000001000001₂₂₆₄  keine Primzahl ?


Die Antwort lautet in Kurzform :  Weil die Anzahl der Nullen zwischen den Einsen ungerade ist. ( 2264  ist dabei die Basis der Zahldarstellung und vollkommen willkürlich gewählt).

Ausführlich lautet die Behauptung :
y₁ = 1 ,  y_n+1 =  y_n + b^k·n  definiert eine Zahlenfolge  y_n , die in Basis  b  geschrieben aus  n  Einsen besteht, zwischen denen Gruppen aus  k - 1  Nullen stehen. (Also ist z.B. für  b = 3  und  k = 2: y₄ = 1010101₃ .) Dann lässt sich zeigen: Für  n > 2  ist  y_n  in allen Basen  b  keine Primzahl, falls  k > 1  gerade ist.

Die Faktorisierung lässt sich konstruktiv angeben. Wie sieht sie in Basis  b  aus ?

Problem 51 stellte einen Spezialfall dieses Problems dar. Den dortigen Lösungsansatz kann man auch hier verwenden, um  y_n  in geschlossener Form darzustellen. Analog zu Problem 51 kann man eine andere (äquivalente) rekursive Definition angeben :

y₁ = 1 ,  y_n+1 = y_n·b^k + 1

Für ungerade  k  gilt die Primzahl-Behauptung nicht. Primzahlen unter den  y_n  sind dann zwar sehr dünn gesät, aber Sie können welche finden. Eine notwendige, aber nicht hinreichende Bedingung ist:  y_n  prim   →   n  prim  (warum?).

Lösung

k/2  ist eine natürliche Zahl, also erhalten wir für  n > 2  die folgende Zerlegung von  y_n  mit Hilfe der geometrischen Reihe :



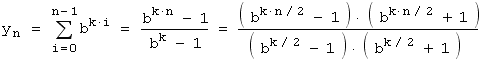
Welche ganzzahligen Faktoren stecken in dieser Zerlegung? Wir setzen zur Abkürzung  x = b^k/2 .

Für  n  ungerade hat  xⁿ ± 1  die Nullstelle  -₊ 1 , ist also durch  x ± 1  teilbar. Somit zerfällt  y_n  in die beiden ganzzahligen Faktoren



Für  n  gerade  hat  xⁿ - 1  die Nullstellen  ± 1 , ist also durch  x² - 1  teilbar. Somit zerfällt  y_n  in die beiden ganzzahligen Faktoren



Damit ist die zentrale Behauptung aus der Problemstellung bewiesen.  -  Für gerade  n  gibt es offenbar noch eine weitere Zerlegung, da  y₂  ebenfalls ein Faktor ist (siehe Problem 51).

Mit der geschlossenen Form aus der geometrischen Reihe für  y_n  lässt sich auch die zweite rekursive Darstellung der Folge  y_n  in der Problemstellung durch Einsetzen leicht nachweisen.


Wie sehen die Faktoren in Basis  b  aus ?  An Beispielen werden einfache Muster deutlich :

Für  b = 7  und  k = 4  ist  y₅ = 10001000100010001₇ = 101010101₇·66006601₇ .

Für  b = 9  und  k = 2  ist  y₇ = 1010101010101₉ = 1111111₉·808081₉ .

Für  k = 4  ist  y₆ = 100010001000100010001_b = 100010001_b·1000000000001_b

      oder  y₆ = 10001_b·10000000100000001_b  (der erste Faktor ist  y₂ ).

Wir wollen die allgemeinen Zerlegungen in Form dieser Beispiele angeben (mit  a = b - 1 ).


n  ungerade :



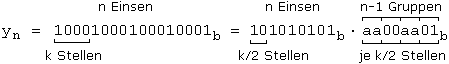
Beweis :  Zur Verdeutlichung schreiben wir die Anzahl der Stellen in den "Gruppen" als oberen Index der Folge. Der erste Faktor auf der rechten Seite ist dann :



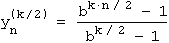
Also ist nur zu zeigen, dass der zweite Faktor gleich



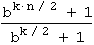
ist. Wir schreiben diesen zweiten Faktor als geometrische Reihe auf:



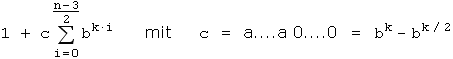
Dann folgt aus



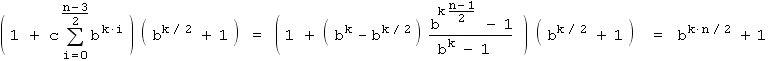
die Behauptung.


n  gerade :


Beweis :  Zu zeigen ist :



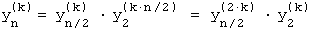
Dies folgt aber direkt aus der Summe der geometrischen Reihe für  y_n . -  Damit ist die Darstellung der Faktorisierung in Basis  b  vollständig.


Hinter der letzten Zerlegung steht die Beobachtung, dass sich bei geradem  n  die Einsen in  y_n  in  n/2  Zweiergruppen teilen lassen. Das lässt sich leicht verallgemeinern :  Ist  n  keine Primzahl, also  n = q·r , so lassen sich die Einsen in  r  Gruppen mit je  q  Einsen teilen. Daraus folgt die schöne Formel, die sich wieder direkt aus der Summe der geometrischen Reihe für  y_n  ergibt :



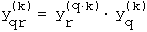
Diese Formel ist auch für  k = 1  richtig (dann besteht  y_n  nur aus Einsen).

Wir hatten uns in der Problemstellung auf  n > 2  beschränkt. Für  n = 2  ist die angegebene Zerlegung nicht möglich, weil einer der Faktoren  1  ist. In der Tat ist etwa  101_b = b² + 1  eine Primzahl für  b = 2, 4, 6, 10, 14, 16, ...

Für  n > 2  können also Primzahlen unter den  y_n  nur bei  n  prim und  k  ungerade vorkommen. Für  k = 1  findet man etliche Primzahlen. Die kleinsten Primzahlen für  k > 1  erhält man mit  n = k = 3 : Dann ist  y₃ = 73, 757, 262657, 1772893  für die Basen  b = 2, 3, 8, 11 . Die dritte dieser Zahlen ist auch  y₃ = 262657  für  k = 9  und  b = 2 .

Publiziert 2010-03-29          Stand 2009-07-19

voriges Problem   |   Liste aller Probleme mit Lösungen   |    nächstes Problem

Manfred Börgens   |    zur Leitseite