Eine Kette hat n Perlen, die je zur Hälfte weiß und schwarz sind. Die Kette kann geschlossen oder offen sein, so wie im folgenden Bild:
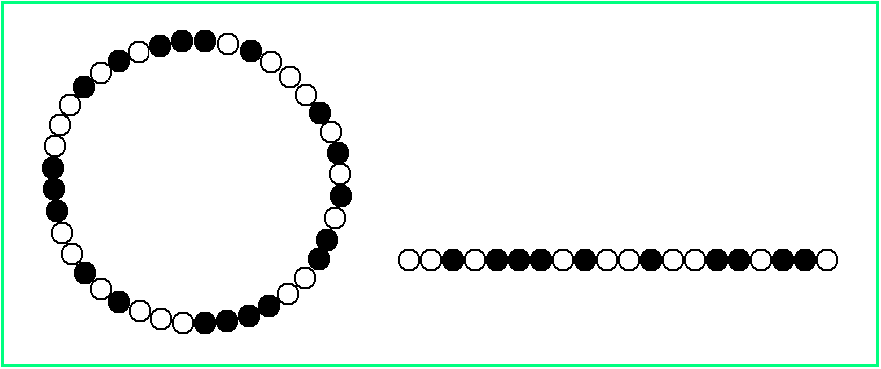
Aus der Kette soll ein zusammenhängendes Teilstück der Länge m geschnitten werden, in dem ebenfalls gleich viele weiße und schwarze Perlen sind. Es stellt sich die Frage, ob das immer geht. Durch Ausprobieren erhält man schnell Gegenbeispiele, z.B. n = 12 , m = 8 für die offene Kette (schreibt man weiße Perlen als 0 und schwarze als 1 , so lässt sich aus der Kette 000111111000 kein Teilstück der Länge 8 schneiden, das je vier weiße und schwarze Perlen enthält).
Wir wollen nun das Problem präzise formulieren. n und m sollen gerade Zahlen sein mit 2 ≤ m < n . Eine Kette (geschlossen oder offen) soll n/2 weiße und n/2 schwarze Perlen enthalten; dabei ist jede Reihenfolge möglich. Das Zahlenpaar (n,m) soll kompatibel heißen, wenn zu jeder Kette der Länge n (n - Kette) ein Teilabschnitt der Länge m (m - Abschnitt) existiert, in dem jeweils m/2 weiße und schwarze Perlen sind. Nicht kompatible Paare (n,m) nennen wir inkompatibel.
Im einfachsten Fall der offenen Kette ist m = n/2 . Dann kann man die n - Kette in zwei disjunkte m - Abschnitte einteilen, und darin liegt auch schon die Beweisidee für (n,m) kompatibel. Das kann man zunächst an kleinen Beispielen wie (n,m) = (8,4) ausprobieren. Eine naheliegende Verallgemeinerung ist dann die Kompatibiltät bei m | n ( m ist Teiler von n ). Wer hierzu einen Tipp haben möchte, kann den Hinweis lesen. Was man aus diesem einfachen Fall lernt, lässt sich mit kleinen Modifikationen auf die folgenden Aussagen anwenden, die bewiesen werden sollen :