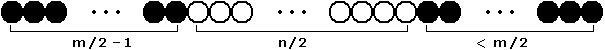Ein Kettenproblem
Die Lösung steht im unteren Teil der Seite.
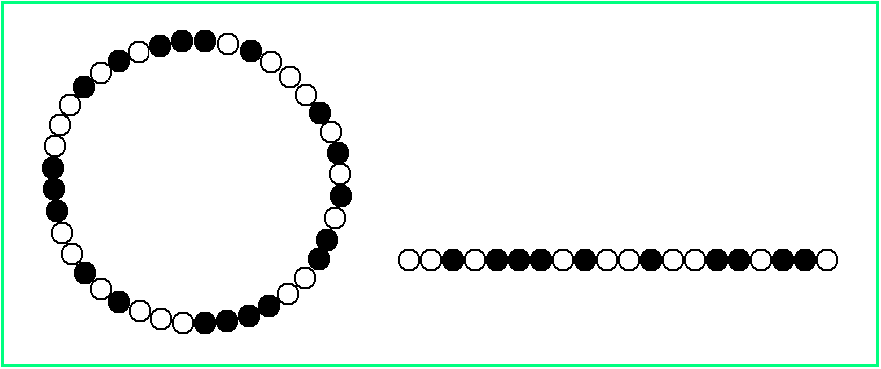
Eine Kette hat n Perlen, die je zur Hälfte weiß und schwarz sind. Die Kette kann geschlossen oder offen sein, so wie im folgenden Bild:
Aus der Kette soll ein zusammenhängendes Teilstück der Länge m geschnitten werden, in dem ebenfalls gleich viele weiße und schwarze Perlen sind. Es stellt sich die Frage, ob das immer geht. Durch Ausprobieren erhält man schnell Gegenbeispiele, z.B. n = 12 , m = 8 für die offene Kette (schreibt man weiße Perlen als 0 und schwarze als 1 , so lässt sich aus der Kette 000111111000 kein Teilstück der Länge 8 schneiden, das je vier weiße und schwarze Perlen enthält).
Wir wollen nun das Problem präzise formulieren. n und m sollen gerade Zahlen sein mit 2 ≤ m < n . Eine Kette (geschlossen oder offen) soll n/2 weiße und n/2 schwarze Perlen enthalten; dabei ist jede Reihenfolge möglich. Das Zahlenpaar (n,m) soll kompatibel heißen, wenn zu jeder Kette der Länge n (n - Kette) ein Teilabschnitt der Länge m (m - Abschnitt) existiert, in dem jeweils m/2 weiße und schwarze Perlen sind. Nicht kompatible Paare (n,m) nennen wir inkompatibel.
Im einfachsten Fall der offenen Kette ist m = n/2 . Dann kann man die n - Kette in zwei disjunkte m - Abschnitte einteilen, und darin liegt auch schon die Beweisidee für (n,m) kompatibel. Das kann man zunächst an kleinen Beispielen wie (n,m) = (8,4) ausprobieren. Eine naheliegende Verallgemeinerung ist dann die Kompatibiltät bei m | n ( m ist Teiler von n ). Wer hierzu einen Tipp haben möchte, kann den Hinweis lesen. Was man aus diesem einfachen Fall lernt, lässt sich mit kleinen Modifikationen auf die folgenden Aussagen anwenden, die bewiesen werden sollen :
- Für geschlossene Ketten sind alle (n,m) kompatibel.
Sei nun die Kette offen.
In den folgenden Fällen ist (n,m) ein kompatibles Paar :
Im folgenden Fall ist (n,m) ein inkompatibles Paar :
Man kann sich also bei weiteren Überlegungen auf m < n/2 beschränken. Dafür gilt, dass (n,m) in den folgenden Fällen kompatibel ist :
Mit diesen Resultaten findet man dann recht schnell inkompatible Paare (n,m) wie z.B. (n,m) = (12,8) (siehe oben) oder mit m = 10 < n/2 . Es empfiehlt sich aber, ein kleines Programm zu schreiben, das die Permutationen der Kettenelemente und die m - Abschnitte überprüft. (Auch für den Fall m = 8 < n/2 , in dem die Kompatibilität gezeigt werden soll, lassen sich zwar mit vertretbarem Aufwand die möglichen Fälle von Hand darstellen, aber der Rechner ist natürlich schneller.) Es stellen sich noch die folgenden Fragen :
- Welches ist das kleinste inkompatible Paar (n,m) ?
- Welches ist das kleinste inkompatible Paar (n,m) mit m < n/2 ?
Wenn man dieses inkompatible Paar gefunden hat, kann man das Ergebnis verallgemeinern, um die letzte Frage zu beantworten :
- Warum gibt es unendlich viele inkompatible Paare (n,m) mit m < n/2 ? (Diese Paare lassen sich konstruktiv angeben.)
Noch ein paar Tipps
Lösung
Die grundlegende Beobachtung bei geschlossenen und offenen Ketten ist : Verschiebt man einen m - Abschnitt um eine Position, so bleibt die Anzahl der weißen (bzw. schwarzen) Perlen entweder gleich oder ändert sich um ± 1 . Macht man mehrere solcher Verschiebungen, kommen alle Anzahlen weißer Perlen zwischen der Anzahl am Anfang (vor den Verschiebungen) und am Ende (nach den Verschiebungen) vor.
Beginnt man beispielsweise mit einem Abschnitt, der 6 weiße Perlen enthält, verrückt dann diesen Abschnitt um beliebig viele Positionen, und zählt dann 13 weiße Perlen, so muss es für jede Zahl k ∈ {6, 7, ... , 13} eine Zwischenposition mit genau k weißen Perlen gegeben haben. Das scheint offensichtlich, soll aber bewiesen werden :
Diskreter Zwischenwertsatz
Eine endliche Folge natürlicher Zahlen ( r - Vektor) beginne mit n1 und ende mit nr . Es sei nr > n1 . Benachbarte Folgenglieder sind entweder gleich oder haben den Abstand 1 . Dann kommt jedes natürliche n zwischen n1 und nr in der Folge vor.
nr > n1 ist keine Einschränkung. Für nr < n1 dreht man die Folge einfach um.
Beweis (Vollständige Induktion über r ; r = 2 klar)
r → r + 1
Zwischen n2 und nr kommen nach Induktionsvoraussetzung alle natürlichen Zahlen vor. Da nur die drei Fälle n1 = n2 , n1 + 1 = n2 und n1 - 1 = n2 in Frage kommen, kommen also insbesondere ab einschl. n2 alle Zahlen von n1 + 1 bis nr vor.
Mit dem Zwischenwertsatz ist nun die Aussage über die geschlossenen Ketten leicht nachweisbar. Wenn man annimmt, dass es keinen m - Abschnitt mit m/2 weißen Perlen gibt, so müssen nach dem Zwischenwertsatz alle m - Abschnitte (o.E.) mehr als m/2 weiße Perlen aufweisen. Es gibt n solcher Abschnitte. Addiert man die Anzahl weißer Perlen über alle Abschnitte, so beträgt die Summe mehr als n·m/2 . Andererseits gibt es in der Kette genau n/2 weiße Perlen, und jede von ihnen kommt in genau m Abschnitten vor, so dass die Summenbildung über die Abschnitte n·m/2 ergeben muss. Also war die Annahme falsch.
Nun zu den offenen Ketten.
Die Kette lässt sich in n/m disjunkte Abschnitte aufteilen. O.E. enthalte der erste Abschnitt mehr als m/2 weiße Perlen. Dann muss es wegen der gleichen Anzahl weißer und schwarzer Perlen in der Kette einen anderen Abschnitt geben, der weniger als m/2 weiße Perlen enthält. Die Behauptung folgt dann aus dem Zwischenwertsatz.
Wir teilen die Kette in drei Teile mit den Längen n/2-1 , 2 , n/2-1 . Der mittlere Teil ist der Überlappungsbereich des ganz linken und des ganz rechten m - Abschnitts. O.E. enthalte wieder der erste m - Abschnitt, bestehend aus den ersten beiden Teilen, mehr als m/2 weiße Perlen.

1. Fall : Der mittlere Teil enthält eine weiße und eine schwarze Perle. Damit enthält der ganz linke m - Abschnitt mehr weiße Perlen als der ganz rechte. Die Behauptung folgt dann aus dem Zwischenwertsatz.
2. Fall : Der mittlere Teil enthält zwei weiße Perlen. Dann enthält der erste Teil mindestens m/2 - 1 weiße Perlen, der letzte somit höchstens m/2 - 2 weiße Perlen. Also enthält der ganz linke m - Abschnitt mindestens m/2 + 1 und der ganz rechte höchstens m/2 weiße Perlen. Die Behauptung folgt aus dem Zwischenwertsatz.
3. Fall : Der mittlere Teil enthält zwei schwarze Perlen. Dann enthält der erste Teil (und damit der ganz linke m - Abschnitt) mindestens m/2 + 1 weiße Perlen, der letzte Teil (und damit der ganz rechte m - Abschnitt) höchstens m/2 - 2 weiße Perlen. Die Behauptung folgt wieder aus dem Zwischenwertsatz.
Man packt alle weißen Perlen in einen mittleren Block, wie im folgenden Bild :
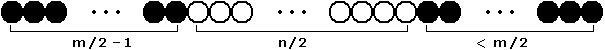
Wegen m < n bleiben für den rechten Teil noch schwarze Perlen übrig; deren Anzahl ist n/2 - m/2 + 1 < m/2 . Ein m - Abschnitt mit m/2 schwarzen Perlen müsste dann den gesamten weißen Abschnitt einschließen und somit mehr als m/2 weiße Perlen. Damit ist die Inkompatibiltät von (n,m) gezeigt.
Ab hier braucht nur noch m < n/2 betrachtet zu werden. Da m | n schon behandelt wurde, muss noch n = 4k + 2 , n ≥ 10 untersucht werden ( k = 1 kann ausscheiden, da in diesem Fall nur m = 2 sein kann). Dann lässt sich die n - Kette wie im folgenden Bild darstellen. Graue Perlen stehen für weiße oder schwarze Perlen.
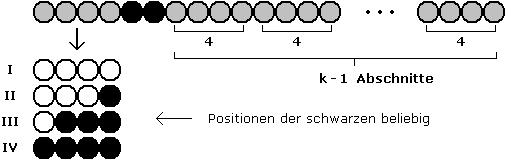
Wenn die linken 4 Perlen gleichverteilt sind ( 2 weiße, 2 schwarze), ist nichts mehr zu beweisen. Also werden nur die vier Alternativen im linken unteren Teil der Graphik untersucht. Sind die beiden folgenden Perlen von verschiedener Farbe, kann man wieder den Zwischenwertsatz anwenden : Dann muss es nämlich in mindestens einem der k - 1 rechten 4 - Abschnitte mehr schwarze Perlen (für die ersten beiden Alternativen) bzw. mehr weiße Perlen (für die letzten beiden Alternativen) geben. Wegen der weiß/schwarz-Symmetrie der vier Alternativen kann o.E. angenommen werden, dass die beiden folgenden Perlen schwarz sind (siehe Graphik).
Zu I : Überschuss an weißen unter den linken 6 Perlen → In einem der rechten 4 - Abschnitte finden sich mehr schwarze als weiße Perlen → Behauptung folgt mit Zwischenwertsatz.
Zu II : Linke 6 Perlen gleichverteilt → Für den Rest gilt m | n - 6 (s.o.).
Zu III und IV : Überschuss an schwarzen unter den linken 6 Perlen → In einem der rechten 4 - Abschnitte finden sich mehr weiße als schwarze Perlen → Behauptung folgt mit Zwischenwertsatz.
Die Fälle m = 6 und m = 8 werden weitgehend analog zu m = 4 behandelt und deshalb etwas komprimiert dargestellt.
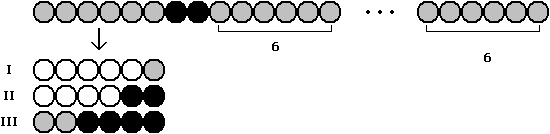
Zu I : Überschuss an weißen unter den linken 8 Perlen → In einem der rechten 6 - Abschnitte finden sich mehr schwarze als weiße Perlen → Behauptung folgt mit Zwischenwertsatz.
Zu II : Linke 8 Perlen gleichverteilt → Für den Rest gilt m | n - 8 .
Zu III : Überschuss an schwarzen unter den linken 8 Perlen → In einem der rechten 6 - Abschnitte finden sich mehr weiße als schwarze Perlen → Behauptung folgt mit Zwischenwertsatz.
Hier müssen zwei Fälle unterschieden werden : 4 schwarze bzw. 3 schwarze Perlen an den Positionen 7 bis 10 .
1. Fall :
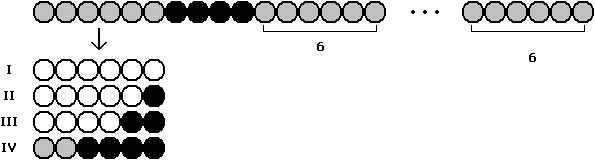
Zu I : Überschuss an weißen unter den linken 10 Perlen → In einem der rechten 6 - Abschnitte finden sich mehr schwarze als weiße Perlen → Behauptung folgt mit Zwischenwertsatz.
Zu II : Linke 10 Perlen gleichverteilt → Für den Rest gilt m | n - 10 .
Zu III : Es gibt 15 mögliche Positionen für die beiden schwarzen Kugeln. Alle ergeben zusammen mit dem angrenzenden schwarzen 4 - Abschnitt einen gleichverteilten 6 - Abschnitt.
Zu IV : Überschuss an schwarzen unter den linken 10 Perlen → In einem der rechten 6 - Abschnitte finden sich mehr weiße als schwarze Perlen → Behauptung folgt mit Zwischenwertsatz.
2. Fall :
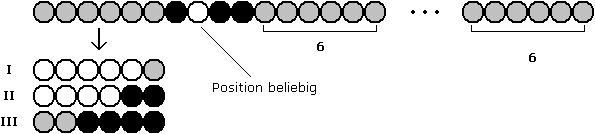
Zu I : Überschuss an weißen unter den linken 10 Perlen → In einem der rechten 6 - Abschnitte finden sich mehr schwarze als weiße Perlen → Behauptung folgt mit Zwischenwertsatz.
Zu II : Linke 10 Perlen gleichverteilt → Für den Rest gilt m | n - 10 .
Zu III : Überschuss an schwarzen unter den linken 10 Perlen → In einem der rechten 6 - Abschnitte finden sich mehr weiße als schwarze Perlen → Behauptung folgt mit Zwischenwertsatz.

Zu I : Überschuss an weißen unter den linken 10 Perlen → In einem der rechten 8 - Abschnitte finden sich mehr schwarze als weiße Perlen → Behauptung folgt mit Zwischenwertsatz.
Zu II : Linke 10 Perlen gleichverteilt → Für den Rest gilt m | n - 10 .
Zu III : Überschuss an schwarzen unter den linken 10 Perlen → In einem der rechten 8 - Abschnitte finden sich mehr weiße als schwarze Perlen → Behauptung folgt mit Zwischenwertsatz.
Hier müssen zwei Fälle unterschieden werden : 4 schwarze bzw. 3 schwarze Perlen an den Positionen 9 bis 12 .
1. Fall :
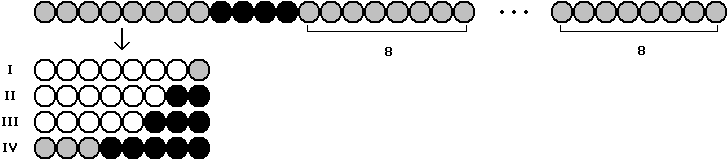
Zu I : Überschuss an weißen unter den linken 12 Perlen → In einem der rechten 8 - Abschnitte finden sich mehr schwarze als weiße Perlen → Behauptung folgt mit Zwischenwertsatz.
Zu II : Linke 12 Perlen gleichverteilt → Für den Rest gilt m | n - 12 .
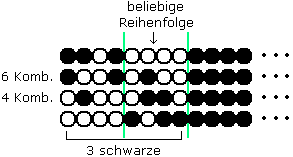
Zu III : Der zweite 4 - Abschnitt von links kann 0 bis 3 schwarze Perlen enthalten, so wie in der folgenden Graphik. Bei 0 und bei 3 schwarzen Perlen ist die Existenz eines gleichverteilten 8 - Abschnitts offensichtlich. In den beiden anderen Fällen muss man nur die 6 bzw. 4 Kombinationen der weißen und schwarzen Perlen im linken 4 - Abschnitt prüfen, um zum gleichen Ergebnis zu kommen.
Zu IV : Überschuss an schwarzen unter den linken 12 Perlen → In einem der rechten 8 - Abschnitte finden sich mehr weiße als schwarze Perlen → Behauptung folgt mit Zwischenwertsatz.
2. Fall :

Zu I : Überschuss an weißen unter den linken 12 Perlen → In einem der rechten 8 - Abschnitte finden sich mehr schwarze als weiße Perlen → Behauptung folgt mit Zwischenwertsatz.
Zu II : Linke 12 Perlen gleichverteilt → Für den Rest gilt m | n - 12 .
Zu III : Überschuss an schwarzen unter den linken 12 Perlen → In einem der rechten 8 - Abschnitte finden sich mehr weiße als schwarze Perlen → Behauptung folgt mit Zwischenwertsatz.
Hier müssen drei Fälle unterschieden werden : 6 , 5 , 4 schwarze Perlen an den Positionen 9 bis 14 .
1. Fall :
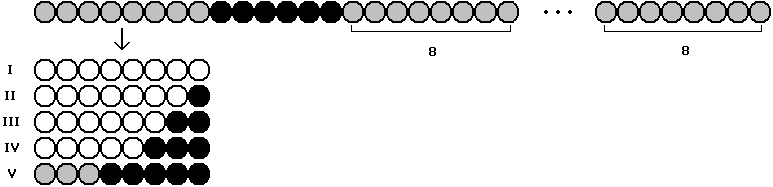
Zu I : Überschuss an weißen unter den linken 14 Perlen → In einem der rechten 8 - Abschnitte finden sich mehr schwarze als weiße Perlen → Behauptung folgt mit Zwischenwertsatz.
Zu II : Linke 14 Perlen gleichverteilt → Für den Rest gilt m | n - 14 .
Zu III : Wie für m = 8 , n = 8k + 4 , 1. Fall III teilt man wieder die linken 8 Perlen in zwei 4 - Abschnitte ; der rechte davon soll 0 , 1 oder 2 schwarze Perlen an beliebiger Position aufweisen. Bei allen drei Möglichkeiten gibt es offensichtlich einen gleichverteilten 8 - Abschnitt innerhalb der linken 14 Perlen.
Zu IV : Dies geht analog zu III, mit 0 , 1 , 2 oder 3 schwarzen Perlen an den Positionen 5 bis 8 . Hier kann man wieder die kleine Graphik aus m = 8 , n = 8k + 4 , 1. Fall III verwenden.
Zu V : Überschuss an schwarzen unter den linken 14 Perlen → In einem der rechten 8 - Abschnitte finden sich mehr weiße als schwarze Perlen → Behauptung folgt mit Zwischenwertsatz.
2. Fall :
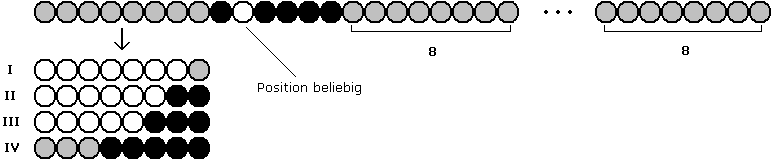
Zu I : Überschuss an weißen unter den linken 14 Perlen → In einem der rechten 8 - Abschnitte finden sich mehr schwarze als weiße Perlen → Behauptung folgt mit Zwischenwertsatz.
Zu II : Linke 14 Perlen gleichverteilt → Für den Rest gilt m | n - 14 .
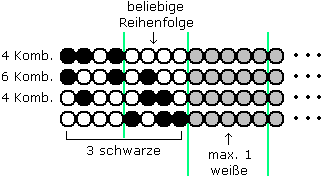
Zu III : Das nächste Bild ist ganz ähnlich wie bei m = 8 , n = 8k + 4 , 1. Fall III. Beim zweiten 4 - Abschnitt von links ist wieder nur die Anzahl schwarzer Perlen von Bedeutung, nicht deren Position. Im linken 4 - Abschnitt muss man dann nur die wenigen möglichen Kombinationen der weißen und schwarzen Perlen durchgehen. Allerdings ist bei jeder dieser Kombinationen zu beachten, dass an einer Stelle des 6 - Abschnitts (Positionen 9 bis 14 ) eine weiße Perle vorkommen muss. Bei der Überprüfung der Kombinationen wird man sehen, dass nur maximal die linken fünf Perlen dieses 6 - Abschnitts für die Auswahl eines gleichverteilten 8 - Abschnitts herangezogen werden müssen; in diesem 5 - Abschnitt (in der Graphik markiert) befindet sich dann eine oder keine weiße Perle.
Zu IV : Überschuss an schwarzen unter den linken 14 Perlen → In einem der rechten 8 - Abschnitte finden sich mehr weiße als schwarze Perlen → Behauptung folgt mit Zwischenwertsatz.
3. Fall :

Zu I : Überschuss an weißen unter den linken 14 Perlen → In einem der rechten 8 - Abschnitte finden sich mehr schwarze als weiße Perlen → Behauptung folgt mit Zwischenwertsatz.
Zu II : Linke 14 Perlen gleichverteilt → Für den Rest gilt m | n - 14 .
Zu III : Überschuss an schwarzen unter den linken 14 Perlen → In einem der rechten 8 - Abschnitte finden sich mehr weiße als schwarze Perlen → Behauptung folgt mit Zwischenwertsatz.
- Welches ist das kleinste inkompatible Paar (n,m) ?
Nach den bisherigen Ergebnissen ist der erste Kandidat (8,6), und dieser erweist sich in der Tat als inkompatibel, wie die Graphik zeigt :

- Welches ist das kleinste inkompatible Paar (n,m) mit m < n/2 ?
Nach den bisherigen Ergebnissen ist der erste Kandidat (22,10). Aber dieses Paar ist kompatibel. Das merkt man zwar nach einigem Probieren, aber den vollständigen Beweis überlässt man am besten einem kleinen Programm. - Der nächste Kandidat ist (24,10), und die Graphik zeigt die Imkompatibilität :

- Warum gibt es unendlich viele inkompatible Paare (n,m) mit m < n/2 ?
Aus der vorigen Frage gewinnt man die Idee, dass Inkompatibiltät sich leicht nachweisen lässt, wenn sich große Abschnitte von weißen Perlen abwechseln mit großen Abschnitten von schwarzen Perlen, so wie in der folgenden Graphik :

In dieser Weise lassen sich beliebig lange Ketten herstellen. Wählt man nun m mit a < m/2 < b , ist das Problem schon gelöst, analog zu der oben gezeigten Kette mit (n,m) = (24,10) und a = 4 , b = 6 .
Man kann das noch etwas detaillierter untersuchen und die Abschnittslängen a und b ausrechnen. Wenn es k Abschnitte der Länge a gibt, gilt a·k = b·(k-1) = n/2 . Insbesondere folgt a = j·(k-1) und b = j·k . Damit lässt sich n darstellen als n = 2·j·k·(k-1) mit j ≥ 2 und k ≥ 3 ( j = 1 scheidet aus wegen a < m/2 < b , k = 2 scheidet aus wegen 2a < m < n/2 ).
Außer den so konstruierten Paaren gibt es noch viele weitere inkompatible mit m < n/2 , da die Abschnitte weißer bzw. schwarzer Perlen für unser Argument nicht exakt gleich lang sein müssen.
Publiziert 2009-12-27 Stand 2009-08-10
voriges Problem | Liste aller Probleme mit Lösungen | nächstes Problem
Manfred Börgens |
zur Leitseite