Eisenbahn-Netzwerk

          Die Lösung steht im unteren Teil der Seite.

Ein Netzwerk von Eisenbahn-Verbindungen lässt sich als Graph darstellen, z.B. wie im folgenden Bild:



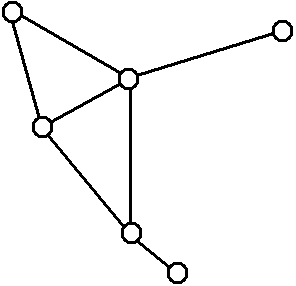
Die Knoten stellen die Bahnhöfe dar. Die Kanten sind die Direktverbindungen zwischen verschiedenen Bahnhöfen. Bahnstrecken zwischen zwei Bahnhöfen A und B, auf denen weitere Bahnhöfe liegen, erhalten also keine eigene Kante von A nach B. Man beachte, dass es auch Kreuzungspunkte von Bahnlinien geben kann, an denen kein Bahnhof liegt, und dass das Netzwerk nicht zusammenhängend sein muss; beides sieht man im folgenden Bild von einem Küstenstaat mit zwei Inseln:




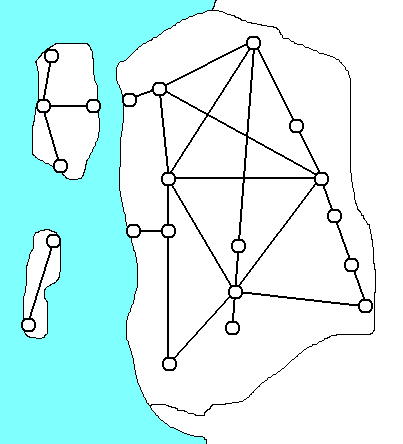
Es soll unterstellt werden, dass es nicht mehrere Direktverbindungen (also Parallelstrecken) zwischen zwei Bahnhöfen gibt.


Wie groß ist die Wahrscheinlichkeit, dass man in einem Netzwerk zwei Bahnhöfe findet, die die gleiche Anzahl von Direktverbindungen zu anderen Bahnhöfen haben ?

Lösung

Zur Problemstellung könnte man einwenden, dass die Wahrscheinlichkeit für eine Direktverbindung (ohne Zwischenstationen) für weiter entfernt liegende Orte kleiner ist als für nahe liegende Orte, und dass man diese Wahrscheinlichkeiten nicht kennt. Insofern erscheint die Aufgabe etwas realitätsfremd. Aber in Wirklichkeit ist diese Aufgabe gar kein Wahrscheinlichkeitsproblem. Wie die beiden Skizzen in der Problemstellung nahelegen, muss man Eigenschaften bestimmter Graphen untersuchen.

Um welchen Graphentyp handelt es sich? Eisenbahn-Netzwerke dieser Art haben eine Reihe spezieller Eigenschaften. Sie sind (in der Terminologie der Graphentheorie):

• ungerichtet (alle Bahnstrecken werden in beiden Richtungen befahren)
• meist nicht vollständig (nicht alle Bahnhöfe sind untereinander direkt verbunden)
• nicht notwendigerweise zusammenhängend
• schlicht (es gibt keine Parallelstrecken und keine "Schleifen", d.h. Strecken, die einen Bahnhof direkt mit sich selbst verbinden)
• es gibt keine isolierten Ecken (Ecken, an die keine Kante grenzt, d.h. Bahnhöfe ohne Anschluss)

Das folgende Bild zeigt nicht erlaubte Bestandteile: isolierte Ecke, Schleife, gerichtete Kante, parallele Kanten.




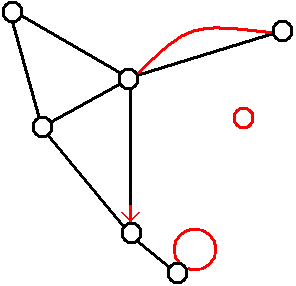
Der graphentheoretische Begriff für die Anzahl der Kanten, die von einer Ecke ausgehen, ist der Grad der Ecke. Isolierte Ecken haben Grad 0. Bei beiden Beispielen in der Problemstellung gibt es jeweils Ecken mit gleichem Grad, d.h. Bahnhöfe mit derselben Anzahl von Direktverbindungen. Es liegt nahe, weitere einfache Beispiele zu untersuchen. Sehr schnell stellt sich die Vermutung ein:

In jedem Eisenbahnnetzwerk gibt es (mindestens) zwei Bahnhöfe mit derselben Anzahl von Direktverbindungen.

Die in der Problemstellung gesuchte Wahrscheinlichkeit ist also  1 .

Dies lässt sich auch leicht beweisen:
In einem Netzwerk mit  n  Bahnhöfen hat jeder Bahnhof zwischen  1  und  n-1  Direktverbindungen. Für den Grad der Ecken gibt es also nur  n-1  Möglichkeiten. Bei  n  Bahnhöfen muss folglich (mindestens) eine dieser Möglichkeiten doppelt (oder mehrfach) vorkommen.

Isolierte Ecken, also Bahnhöfe ohne Anschluss, hätte man nicht ausschließen müssen. Denn der Beweis lässt sich für diesen Fall modifizieren: Wären alle Grade der  n  Ecken verschieden, so käme jeder Grad von  0  bis  n-1  je einmal vor. Dann müsste aber der Bahnhof mit den  n-1  Direktverbindungen mit allen anderen Bahnhöfen verbunden sein, also könnte Grad  0  nicht vorkommen.

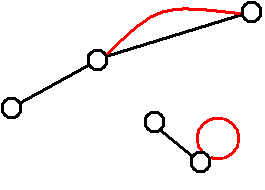
Dagegen versagt die Argumentation bei Parallelstrecken oder Schleifen, wie man an den beiden folgenden Mini-Netzwerken sieht, in denen alle Ecken verschiedene Grade haben:

Publiziert 2006-06-14          Stand 2005-09-13

voriges Problem   |    Liste aller Probleme mit Lösungen   |    nächstes Problem