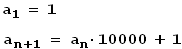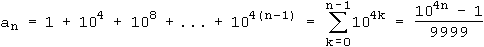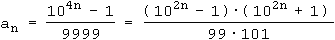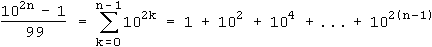Primzahlenfreie Zahlenfolge
Die Zahlenfolge an wird rekursiv definiert:
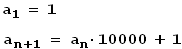
Es ist zu zeigen, dass diese Folge keine Primzahlen enthält.
Es gibt einen konstruktiven Beweis, d.h. zu jedem an lässt sich ein echter Teiler angeben. Wer dabei nicht weiterkommt, kann einen Tipp nachlesen.
Lösung
Die Folge beginnt mit
1, 10001, 100010001, 1000100010001, ...
1 ist keine Primzahl, und 10001 auch nicht, da 10001 = 73·137 . Für gerade n kommen in an eine gerade Anzahl Einsen vor. Offenbar ist also 10001 ein Teiler aller dieser an .
Für ungerade n schreibt man an als geometrische Reihe:
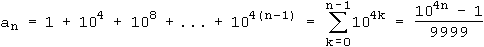
Man muss also in diesem Bruch nach Teilern suchen. Nach der dritten binomischen Formel ergibt sich die folgende Zerlegung:
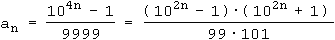
Die 99 wurde nicht weiter zerlegt, da sie - in Analogie zu der Reihe für an - offenbar mit dem ersten Faktor des Zählers wieder zu einer abbrechenden geometrischen Reihe gehört:
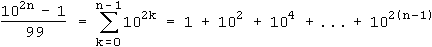
Der gefundene Faktor ist also für n = 3, 5, 7, ... :
10101, 101010101, 1010101010101, ...
Diese Zahlen sind allerdings nur dann Teiler von an , wenn (102n + 1)/101 eine natürliche Zahl ist. Dies gilt sicherlich für n = 1 ; für größere ungerade n geht der Nachweis induktiv:
Sei bn = 102n + 1 durch 101 teilbar. Die Differenz zu bn+2 beträgt 102n · 9999 und ist durch 101 teilbar. Also ist auch bn+2 durch 101 teilbar.
Publiziert 2005-06-12 Stand 2005-04-17
voriges Problem | Liste aller Probleme mit Lösungen | nächstes Problem
Manfred Börgens | zur Leitseite