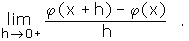| Manfred Börgens Mathematik auf Briefmarken # 35 |
Liste aller Briefmarken vorige Marke nächste Marke |
zur Leitseite |

Die Jensen'sche Ungleichung
nach Johan Ludwig Jensen (1859 - 1925)
Statt einer Briefmarke wird in diesem Monat ein Stempel gezeigt. Es ist außergewöhnlich, dass eine mathematische Formel mit Hilfe einer Frankiermaschine in großer Zahl auf die Reise in alle Welt geschickt wird. Dass es sich um einen dänischen Stempel handelt, ist nicht verwunderlich, wenn man die Formel erkennt: Es ist die Ungleichung, die der Däne Johan Ludwig Jensen 1906 für konvexe Funktionen aufgestellt hat.
J. L. Jensen studierte Mathematik und Naturwissenschaften an einem Polytechnikum in Kopenhagen und arbeitete danach bis zu seiner Pensionierung bei der Kopenhagener Telefongesellschaft, zunächst als Fernmeldeingenieur und ab 1890 als Abteilungsleiter für Fernmeldetechnik. Mathematik betrieb er in seiner Freizeit, erreichte aber ein so hohes Niveau, dass seine Forschungsergebnisse in namhaften mathematischen Zeitschriften gedruckt wurden.
Die Funktion φ in der Ungleichung ist eine reelle Funktion, definiert auf einem Intervall. Die Ungleichung gilt genau dann, wenn φ eine konvexe Funktion ist. Üblicherweise wird die Definition für Konvexität mit der Ungleichung
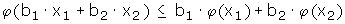
gegeben, wobei x1 und x2 beliebige Punkte aus dem Definitionsintervall und b1 , b2 beliebige positive Zahlen mit der Summe 1 sein können. Die Bedeutung dieser Definition kann man sich zunächst anhand eines einfachen Spezialfalls veranschaulichen. Wählt man b1 = b2 = 1/2 , so lautet die Ungleichung
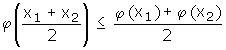
Diese Ungleichung ist in der Jensen'schen Ungleichung auf dem Stempel enthalten; man muss dort nur eine Summe mit genau zwei Summanden nehmen und a1 = a2 = 1 . Bild 1 zeigt die Lage aller Punkte in der Ungleichung; zur Abkürzung sind dort die φ-Funktionswerte von x1 und x2 mit y1 und y2 bezeichnet:
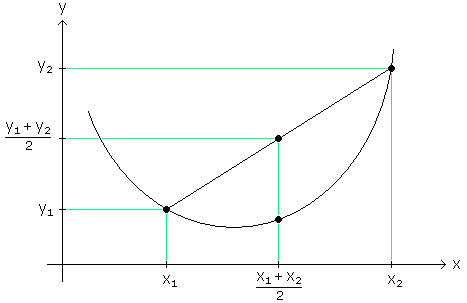
Bild 1
Für diesen Spezialfall bedeutet also die Jensen'sche Ungleichung, dass der Mittelpunkt der Sehne zwischen zwei Kurvenpunkten oberhalb des zugehörigen Funktionswertes liegt.
("oberhalb" soll hier und im Folgenden nicht ausschließen, dass die beiden betrachteten Punkte zusammenfallen; in den Ungleichungen wird ja kein striktes "<" verlangt. - Der Graph der Funktion wird hier der Einfachheit halber immer als "Kurve" bezeichnet.)
Auch die schon genannte Definition der Konvexität
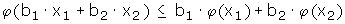
lässt sich graphisch gut veranschaulichen:
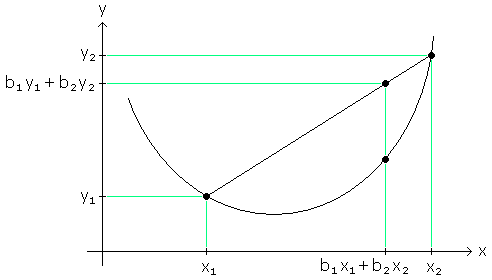
Bild 2
Bild 2 zeigt, dass beliebige Sehnenpunkte immer oberhalb der zugehörigen Kurvenpunkte liegen; dies ist die "graphische Definition" der Konvexität reeller Funktionen.
Die Definition mit b1 und b2 ist äquivalent zur Jensen'schen Ungleichung für zwei Summanden:
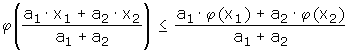
Gilt nämlich diese Jensen'sche Ungleichung, so folgt die Definition, wenn man a1 = b1 und a2 = b2 wählt; die Summen in den Nennern der Jensen'schen Ungleichung sind dann 1 . Gilt umgekehrt die Ungleichung aus der Definition, so wählt man b1 = a1 / ( a1 + a2 ) und b2 = a2 / ( a1 + a2 ) und erhält die Jensen'sche Ungleichung für zwei Summanden.
Durch vollständige Induktion erhält man schließlich die Jensen'sche Ungleichung für mehrere Summanden wie auf dem Stempel. Hier ist der Induktionsschritt von n auf n + 1 Summanden:
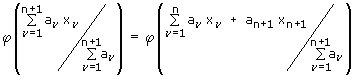
Dieser Ausdruck wird umgeformt, indem man zur Abkürzung
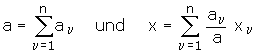
setzt und mit 1/a erweitert:
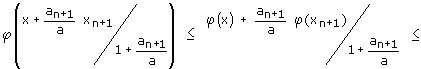
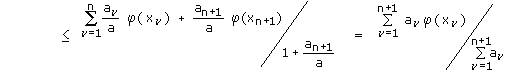
Also ist die Jensen'sche Ungleichung auf dem Stempel eine äquivalente Beschreibung der Konvexität von φ .
Die Jensen'sche Ungleichung kann man sich veranschaulichen als eine Aussage über den Schwerpunkt von Punkten auf der Kurve. Versieht man Punkte ( xv , yv ) in der Ebene mit "Gewichten" av (in Bild 3 als grüne Säulen dargestellt), so liegt ihr gemeinsamer Schwerpunkt in
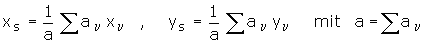
Die Jensen'sche Ungleichung sagt also für Punkte ( xv , yv ) auf einer konvexen Kurve aus:
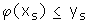
Der Schwerpunkt gewichteter Punkte auf einer konvexen Kurve liegt oberhalb der Kurve.
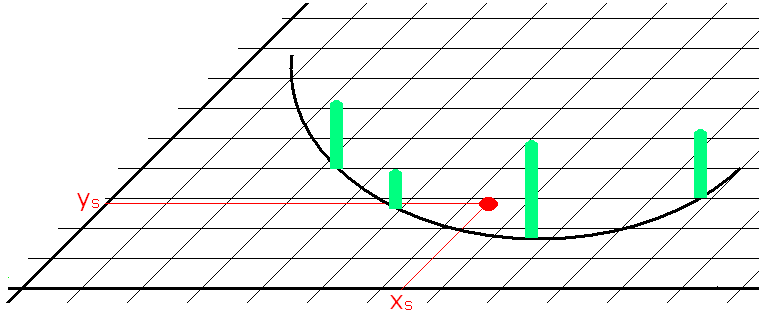
Bild 3
Den schönen Stempel mit der Jensen'schen Ungleichung verdanke ich Herrn Professor Dr. Jacobus van Lint von der Universität Eindhoven. Er ist so wie ich Mitglied der Mathematical Study Unit und hat mir vor einigen Monaten eine große Freude gemacht, als er mir ein dickes Paket mit vielen mathematischen Stempeln schickte. - Professor van Lint ist den Teilnehmern des Mathematischen Weltkongresses 1998 in Berlin sicherlich noch bekannt durch seinen bemerkenswerten Vortrag "The mathematics of the CD-player". - Dem freundlichen Kollegen J. van Lint sei an dieser Stelle noch einmal herzlich gedankt.
Von Prof. van Lint stammt auch ein eleganter und sehr anschaulicher Beweis für die Stetigkeit konvexer Funktionen auf offenen Intervallen. Voraussetzung dafür ist die oben angegebene Definition
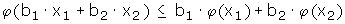
Dies muss deshalb ausdrücklich erwähnt werden, weil in manchen Lehrbüchern die Definition
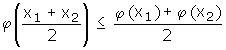
für die Konvexität verwendet wird, und in diesem Fall die Stetigkeit nicht folgt.
Nun zum Beweis: Die Stetigkeit im Punkt x soll gezeigt werden. h > 0 wird so gewählt, dass x + h und x - h im Definitionsintervall liegen. Für die Werte x, x + h, x - h laufe die Kurve durch die Punkte A, B, C . In Bild 4 kann die Kurve wegen der Konvexität nur durch die weißen, aber nicht durch die blauen Bereiche laufen:
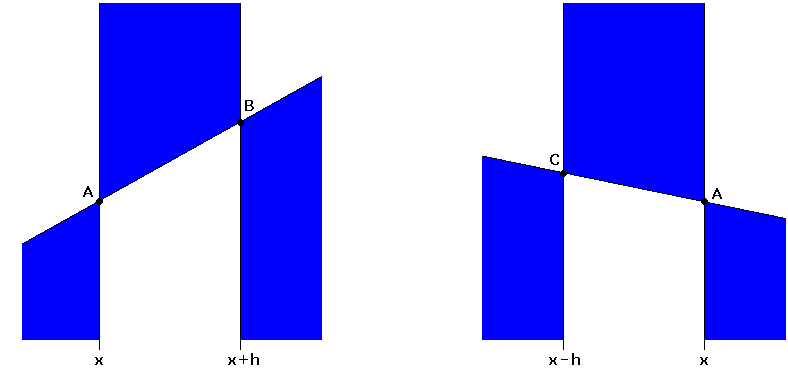
Bild 4
(Natürlich muss die Strecke AB nicht notwendigerweise eine positive Steigung haben bzw. CA eine negative. A muss lediglich unterhalb oder auf CB liegen.)
In Bild 5 werden beide Skizzen aus Bild 4 kombiniert:
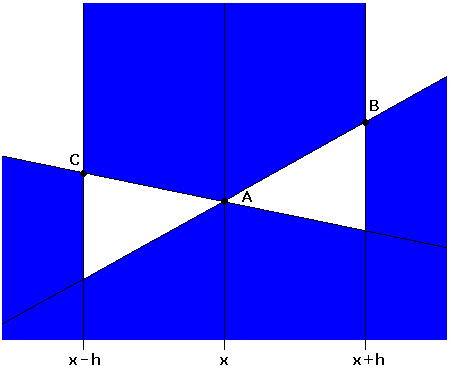
Bild 5
In einer Umgebung von x verläuft also der Graph in einem "Trichter", woraus sofort die Stetigkeit folgt.
Der van Lint'sche Beweis umfasst noch mehr: Aus Bild 5 folgt auch die rechts- und linksseitige Differenzierbarkeit konvexer Funktionen auf offenen Intervallen. Es genügt, den rechtsseitigen Fall zu betrachten. Die Steigung der Strecke AB ist:
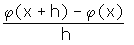
Für 0 < h' < h und den zu x + h' gehörigen Kurvenpunkt B' ist wegen der Konvexität die Steigung der Strecke AB' kleiner oder gleich der Steigung von AB :
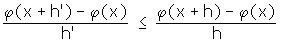
Also ist
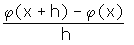
monoton fallend, wenn h > 0 gegen 0 strebt. Aus Bild 6 erkennt man außerdem, dass die Steigung von AB' für alle h' nach unten durch die Steigung der Strecke AD beschränkt ist:
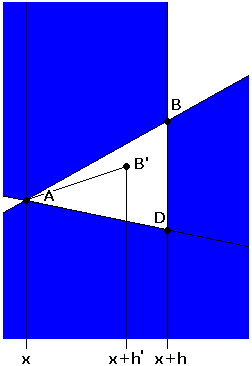
Bild 6
Folglich existiert der Grenzwert (rechtsseitige Ableitung)