
Michel 1273
Scott 579
"Drei Dinge sind mir zu wunderlich, (...)
des Adlers Weg im Himmel,
der Schlangen Weg auf einem Felsen,
des Schiffs Weg mitten im Meer, (...)"
Salomon
Sprüche 30, 18-19
| Manfred Börgens Mathematik auf Briefmarken # 31 |
Liste aller Briefmarken vorige Marke nächste Marke |
zur Leitseite |
 |
Belgien 1962 Michel 1273 Scott 579 |
"Drei Dinge sind mir zu wunderlich, (...) des Adlers Weg im Himmel, der Schlangen Weg auf einem Felsen, des Schiffs Weg mitten im Meer, (...)" Salomon Sprüche 30, 18-19 |
Gerhard Mercator (1512 - 1594)
Im 15. und 16. Jahrhundert entdeckten und eroberten europäische Seefahrer eine Vielzahl unbekannter und entlegener Länder. Der Bedarf an guten Land- und Seekarten stieg stark an. Gerhard Mercator wurde in dieser Zeit mit seinen Karten, Atlanten und Globen weltbekannt.
Die Kartographie hat eine mathematische Basis, denn zur Herstellung einer Karte wird eine Abbildung der Erdoberfläche - näherungsweise also einer Kugel oder eines Rotationsellipsoiden bzw. eines Teils davon - auf eine Ebene benötigt. Diese Abbildung soll geeignet sein für die praktische Nutzung, d.h. sie soll das Bild der Erde möglichst verzerrungsfrei darstellen. Nun ist aber nicht offensichtlich, was genau mit "verzerrungsfrei" gemeint ist: Soll die Karte "längentreu" sein, d.h. sollen Abstände zwischen Punkten auf der Karte die tatsächlichen Entfernungen auf der Erde maßstäblich wiedergeben? Oder soll die Karte "flächentreu" sein, d.h. sollen gleiche Flächeninhalte auf der Erde in gleiche Flächeninhalte auf der Karte verkleinert werden? Schließlich ist noch die "Winkeltreue" von Bedeutung; hierbei sollen die Schnittwinkel sich schneidender Kurven bei der Abbildung von der Erdkugel auf die ebene Karte erhalten bleiben. - Am besten wäre es natürlich, wenn man alle diese Eigenschaften in einer Karte vereinigen könnte, aber schon der Blick in einen Atlas lässt einen vermuten, dass die Kartographen zu Kompromissen gezwungen sind. Woran liegt das?
Mathematische Abbildungen, an die solche Forderungen der Verzerrungsfreiheit gestellt werden können, gehören in das Gebiet der Differentialgeometrie, die sich erst nach der Entdeckung der Infinitesimalrechnung im 17. Jahrhundert entwickeln konnte, also zu Mercators Zeiten noch nicht zur Verfügung stand. Mit den Mitteln der Differentialgeometrie lässt sich beweisen, dass den Schwierigkeiten der Kartographen aller Epochen mit Längen-, Flächen- und Winkeltreue mathematische Ursachen zu Grunde liegen. Die tatsächlichen Möglichkeiten für verzerrungsfreie Kartengestaltung sind nämlich sehr ernüchternd: Längentreue Karten gibt es nicht. Flächen- und Winkeltreue sind einzeln möglich, schließen sich aber gegenseitig aus.
Die Kunst des Kartographen besteht also u.a. darin, entweder eine flächentreue oder winkeltreue Abbildung der Erdoberfläche auf die ebene Karte zu konstruieren oder Abbildungen zu finden, die Längen-, Flächen- und Winkeltreue jeweils in möglichst hohem Maße aufweisen, was bei der Darstellung kleiner Gebiete auch gelingt.
Gerhard Mercator (latinisiert aus seinem Geburtsnamen Kremer) wurde wenige Jahre nach der Entdeckung Amerikas in Flandern geboren und studierte an der Universität Löwen Philosophie und Mathematik. Er wurde ein Landmesser, Instrumentenbauer und Kartograph von Weltruf. Mercator lebte ab 1552 in Duisburg und wurde "Hofkosmograph" seines Landesherrn, des Herzogs von Kleve.
Nach Gerhard Mercator ist die "Mercator-Projektion" benannt. Dies ist eine spezielle und noch heute verbreitete winkeltreue Abbildung, die Mercator vor allem für die Benutzung unter Seeleuten entwickelt hat. Warum war gerade die Winkeltreue von Karten für die Seefahrt interessant?
Will man mit einem Schiff vom Ort A zum Ort B fahren und dabei die kürzeste Route nehmen, so ändert sich permanent der Kurswinkel (d.h. die Kompassrichtung). Ausnahmen bilden lediglich Fahrten in Nord-Süd-Richtung oder auf dem Äquator (denn kürzeste Verbindungen auf der Kugel verlaufen immer entlang von "Großkreisen", also Kurven, die einen vollen Kugelumfang umlaufen). Solche Kurse waren für die Navigatoren früherer Zeiten nur sehr schwer zu berechnen und einzuhalten. Viel einfacher war es, einen Kurs zu wählen, bei dem das Schiff immer in die gleiche Himmelsrichtung fahren konnte, auch wenn dies eine längere Fahrtstrecke bedeutete. Nun könnte man meinen, dass dazu nur auf einer Karte nachgeschaut werden braucht, in welcher Richtung der Ort B von A aus liegt. Aber das gibt bei den meisten Karten ein falsches Ergebnis, nur winkeltreue Karten zeigen die richtige Richtung an.
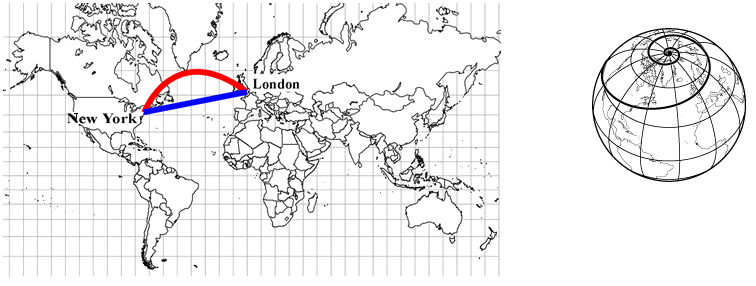
Bild 1
Bild 1 zeigt eine solche winkeltreue Karte. Die rote Linie beschreibt die kürzeste Verbindung, sie ist Teil eines Großkreises. Die blaue Linie beschreibt die Route unter konstanter Kompassrichtung. Überträgt man eine solche Linie (verlängert in beide Richtungen) in eine Kurve auf dem Globus, erhält man eine Spirale wie im rechten Teil von Bild 1.
Gerhard Mercator stellte sich die Aufgabe, eine winkeltreue Zylinderprojektion für die Kugel zu konstruieren. Zylinderprojektionen findet man in Kartenwerken recht häufig; dabei wird (fast) jeder Punkt der Erde mit genau einem Punkt auf dem Zylinder identifiziert; durch senkrechtes Aufschneiden des Zylinders erhält man eine Karte. Beim Standardfall der Zylinderprojektion (Bild 2) liegt die Erde verkleinert innerhalb des Zylinders und berührt ihn entlang des Äquators; alle Meridiane (Längenkreise) werden als senkrechte parallele Geraden auf den Zylinder projiziert, alle Breitenkreise als waagerechte parallele Kreise, die dann auf der ebenen Karte als parallele Geradenstücke erscheinen. Meridiane haben dann auf dem Zylinder die gleichen Abstände, die sie auf dem Äquator der Kugel haben. Dagegen ist zunächst offen, welchen Abstand die Breitenkreise auf dem Zylinder haben sollen, und in der Tat werden dafür verschiedene Möglichkeiten verwendet. - Die Pole werden bei dieser Zylinderprojektion nicht dargestellt. - In Bild 2 sind zwei Meridiane und ein Breitenkreis auf der Kugel in grün eingezeichnet und ihre Abbilder auf dem Zylinder in blau.
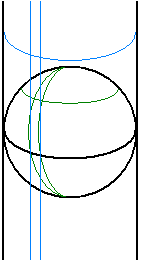
Bild 2
Verwendet man auf der Kugel die geodätischen Koordinaten φ für die geographische Länge und δ für die geographische Breite ( φ macht dabei einen Komplettumlauf von 0° bis 360° in West-Ost-Richtung, δ durchläuft auf der Nordhalbkugel 0° bis 90° und auf der Südhalbkugel 0° bis -90°), so ist φ unverändert auf den Zylinder übertragbar, und statt der Breite δ muss eine Höhe h = m(δ) festgelegt werden. Der Einfachheit halber wird man am Äquator h = 0 = m(0) wählen und ansonsten für h das gleiche Vorzeichen wie für δ . Bei der Beschriftung der Karte wird man aber wieder δ statt h eintragen, damit die Beziehung zu den vertrauten geodätischen Koordinaten erkennbar bleibt.
Mercators Problem bestand also darin, die mathematische Funktion m so zu bestimmen, dass die zugehörige Karte winkeltreu ist. Insbesondere lassen sich dann alle Wege, die immer in gleicher Kompassrichtung verlaufen, auf der Karte als Geradenstücke zeichnen. Das erweist sich aber als keine ganz leichte Aufgabe. Möchte man nämlich einen Winkel auf einer Karte messen, so muss man den Maßstab der Karte in Nord-Süd- und in West-Ost-Richtung kennen. In Bild 3 ist ein Kartenpunkt ( φ , δ ) eingezeichnet, durch den eine Gerade g verläuft. Der Winkel α , den g mit dem Meridian bildet, ist aus dem Zusammenhang tan(α) = dφ / dδ zu berechnen, aber nur, wenn die kleinen Stücke dφ und dδ den gleichen Maßstab aufweisen.
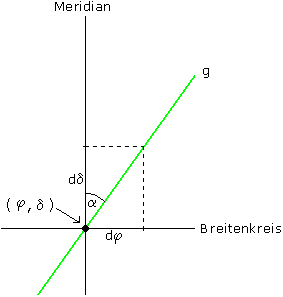
Bild 3
Wie steht es also mit den Maßstäben bei der Zylinderprojektion? Da es keine längentreuen Karten gibt, gibt es für eine Karte gar keinen Maßstab. Für Karten, die die Erdkugel "im Kleinen" sehr genau abbilden, kann man aber lokal einen näherungsweisen Maßstab angeben. Für die Nord-Süd-Richtung können wir bei der Zylinderprojektion noch nichts sagen, da die Funktion m noch ungewiss ist. Aus dem Erdquerschnitt in Bild 4 kann man entnehmen, dass auf einer Einheitskugel (Radius 1) der δ-Breitenkreis den Radius cos δ hat. Während also auf der Erde der δ-Breitenkreis den (cos δ)-fachen Umfang gegenüber dem Äquator aufweist, sind die beiden auf der Karte gleich lang (siehe Bild 2). Anders ausgedrückt: Misst man auf der Karte ein kleines Stück dφ in West-Ost-Richtung wie in Bild 3, so ist es gegenüber einem entsprechenden Stück auf dem Kartenäquator um den Faktor 1/cos φ zu lang. Jetzt kommt die Schlussfolgerung, die auch Mercator zu seiner Karte geführt hat: Damit die Winkelberechnung überall auf der Karte in gleicher Weise durchgeführt werden kann, und damit das Größenverhältnis von dφ zu dδ dem auf der Erdkugel entspricht, muss das Meridianstück dδ ebenfalls um den Faktor 1/cos δ gelängt werden.
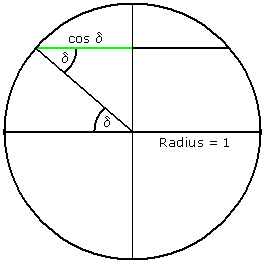
Bild 4
Da sich dδ kontinuierlich zwischen dem Äquator und den Polen verändert, ist eine schrittweise Anpassung (mit dem Faktor 1/cos δ ) von kleinen Stücken dδ auf den Meridianen natürlich nur eine Näherungslösung des Problems der winkeltreuen Zylinderprojektion. Gerhard Mercator konnte mehr nicht erreichen. Er unterteilte seinen Kartenentwurf mit Breitengraden im 1°-Raster. Deren Abstände auf der Kugel betragen π/180, wenn man der Einfachheit halber den Kugelradius auf 1 normiert, was auf eine Karte der Breite 2·π führt. (Diese Abstände gelten ebenfalls für die Längengrade sowohl auf dem Zylinder als auch auf dem Äquator der Kugel.) Statt des Abstandes π/180 hat Mercator (π/180)/cos δ gewählt, wobei er immer das δ "halbgradig" genommen hat, also in der Mitte zwischen zwei Breitengradlinien. Es ist nicht anzunehmen, dass er sich einer Cosinus-Tabelle bedient hat. Er wird wohl rein geometrisch gearbeitet haben; die für die Kartenherstellung erforderlichen Stücke (π/180)/cos δ kann er z.B. wie in Bild 5 erzeugt haben. Dort ist das große rechtwinklige Dreieck mit der senkrechten blauen Linie als Gegenkathete ähnlich zum kleinen blauen Dreieck. a ist ein Meridianstück, hier vereinfacht zu einer geraden Strecke - bei Mercator würde es 1° entsprochen haben. Die durch die Skizze dargestellte Strecke b wird dann auf der Karte abgetragen (statt a ) - bei Mercator also als Abstand zwischen den Breitengradlinien für δ - 0,5 und δ + 0,5 .
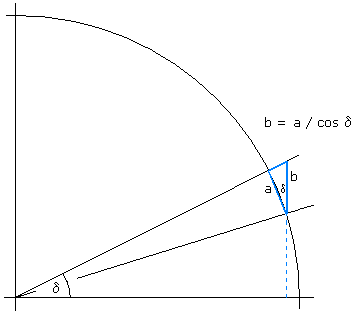
Bild 5
Wie sieht eine "Mercator-Karte" aus? Zunächst erkennt man (siehe Bild 6) das für Zylinderprojektionen typische rechtwinklige Raster von Längen- und Breitengraden. Da zu den Polen hin der Faktor 1/cos δ gegen Unendlich strebt, werden die Abstände der Breitengrad-Linien zunehmend größer. Die Umgebungen der Pole werden also auf der Mercator-Karte nicht abgebildet. Länder weit im Norden oder Süden sind viel größer abgebildet als solche in Äquatornähe, denn sowohl ihre West-Ost- als auch ihre Nord-Süd-Ausdehnung ist (schrittweise) durch den Faktor 1/cos δ gestreckt worden. Wollte man die ganze Erde abbilden (ohne die Pole), so würden Zylinder und Karte unendlich hoch.
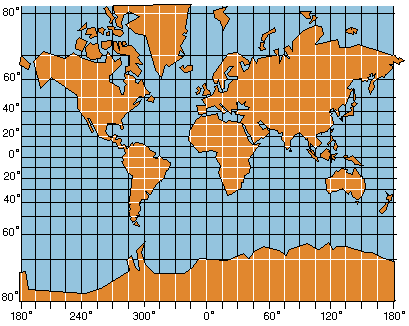
Bild 6
Ein Seefahrer kann nun auf einer Mercator-Karte seinen Start- und Zielort durch eine gerade Strecke verbinden; den Kurswinkel α kann er dann wie in Bild 3 messen. Auf der Erdkugel ist die zugehörige Route eine Kurve, die alle Meridiane unter dem gleichen Winkel α schneidet, also immer in der gleichen Kompassrichtung folgt. Eine solche Kurve auf der Kugel heißt Loxodrome (siehe Bild 1, rechts). Diese Kurve war schon einige Jahre vorher von dem portugiesischen Mathematiker Pedro Nunes beschrieben und für die Seefahrt empfohlen worden. Für einen kleinen Gebietsausschnitt ist in Bild 7 ein Stück dieser Loxodrome dem entsprechenden Kartenausschnitt (wie in Bild 3) gegenüber gestellt.
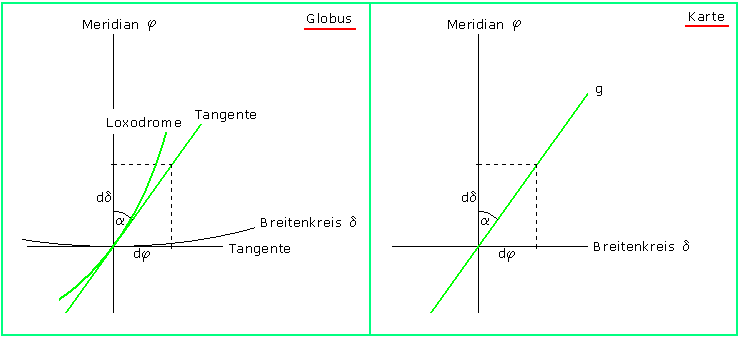
Bild 7
Auf der Kugel (Bild 7, links) wird der Winkel α zwischen dem Meridian und der Tangente an die Loxodrome genommen; für kleine Stücke dφ und dδ ist das näherungsweise der gleiche Winkel wie auf der Karte (Bild 7, rechts).
Es wurde schon erwähnt, dass die Loxodrome nicht den kürzesten Weg zwischen zwei Punkten beschreibt. Vor allem weite Reisen in West-Ost-Richtung, weit weg vom Äquator, werden durch diese Kurswahl erheblich länger. Zu den Polen hin wickelt sich die Loxodrome spiralig auf (siehe Bild 1).
Wie ging es nach Mercator weiter mit seiner Projektion? Wir haben immer noch nicht die Funktion m berechnet, die auf der Karte den Abstand h der Breitengradlinien vom Äquator angibt. Dies war Mercator nicht möglich, da er noch nicht über die Mittel der Infinitesimalrechnung verfügen konnte. Bei ihm war der Breitengrad δ (hier ganzzahlig und im °-Maß) vom Äquator
(π/180)(1/cos 0,5° + 1/cos 1,5° + ... +1/cos (δ-0,5)°)
entfernt, und man sieht, dass dieser Ausdruck bei zunehmend feinerer Teilung als Grenzwert das Integral hat:
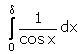
Dieses Integral findet man in jeder Integraltafel mit dem Ergebnis:
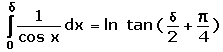
Damit ist die gesuchte Funktion m gefunden. Auf der Mercator-Karte hat der Breitengrad δ vom Äquator den Abstand

Mercator-Schatzkammer im Kultur- und Stadthistorischen Museum Duisburg
Loxodromen (hervorragende Darstellung der zugrundeliegenden Mathematik, insbesondere Berechnung loxodromischer Winkel und Distanzen; Rolle des Pioniers Pedro Nunes)
Kategorie: Geomathematik