Briefmarken des Monats Dezember 2002

  Rumänien 1960 und UdSSR 1956

  Michel 1895 und 1830
  Scott 1345 und 1822

Begründer der nichteuklidischen Geometrie:

Janos Bolyai (1802-1860)

Nikolai Iwanowitsch Lobatschewski (1792-1856)

beide Marken zum 100. Todestag herausgegeben

Beide Mathematiker werden in diesem Dezember mit einer Monatsbriefmarke für einen Jahrestag geehrt: Janos Bolyai zum 200. und Nikolai Lobatschewski zum 210. Geburtstag. Der Ungar Bolyai wurde am 15.12.1802 in Kolozsvar (heute Cluj in Rumänien) geboren, der Russe Lobatschewski am 1.12.1792 in Nishni Nowgorod (am 20.11. nach dem damals in Russland noch gültigen julianischen Kalender).

Die ebene euklidische Geometrie ist eine der fundamentalen mathematischen Disziplinen, Grundlage für Schulgeometrie und technisches Zeichnen, unentbehrlich für die Darstellung von physikalischen und ingenieurwissenschaftlichen Sachverhalten. Euklid gab der Geometrie eine (für seine Zeit) strenge wissenschaftliche Basis, indem er Definitionen, Axiome und Postulate an ihren Anfang stellte.

Die fünf euklidischen Postulate sind für die Entwicklung der Geometrie von besonderer Bedeutung; sie lauten:

1. Es soll gefordert werden, dass sich von jedem Punkte nach jedem Punkte eine gerade Linie ziehen lasse.


2. Ferner, dass sich eine begrenzte Gerade stetig in gerader Linie verlängern lasse.


3. Ferner, dass sich mit jedem Mittelpunkt und Halbmesser ein Kreis beschreiben lasse.


4. Ferner, dass alle rechten Winkel einander gleich seien.


5. Endlich, wenn eine Gerade zwei Geraden trifft und mit ihnen auf derselben Seite innere Winkel bildet, die zusammen kleiner sind als zwei Rechte, so sollen die beiden Geraden, ins Unendliche verlängert, schließlich auf der Seite zusammentreffen, auf der die Winkel liegen, die zusammen kleiner sind als zwei Rechte.

Das fünfte Postulat ist das berühmte Parallelenpostulat (häufig auch Parallelenaxiom genannt), denn es lässt sich zeigen, dass es äquivalent mit der folgenden Formulierung ist:

   5'.  Zu jeder Geraden verläuft durch jeden Punkt, der nicht auf der
           Geraden liegt, höchstens eine Parallele.

In 5'. bedeutet "Parallele" eine Gerade, die die vorgegebene Gerade nicht schneidet. Zusammen mit den anderen Postulaten, Definitionen und Axiomen Euklids folgt dann aus 5. bzw. 5'.:

In der ebenen euklidischen Geometrie gilt: Zu jeder Geraden verläuft durch jeden Punkt, der nicht auf der Geraden liegt, genau eine Parallele.

Über 2000 Jahre lang hat man versucht zu beweisen, dass das Parallelenpostulat aus den anderen Postulaten folgt, also als Postulat auch weggelassen werden könnte. Alle diese Beweisversuche schlugen fehl, aber erst Bolyai und Lobatschewski führten (unabhängig voneinander) Geometrien ein, in denen das euklidische Parallelenpostulat nicht gilt, sondern durch eine andere Aussage ersetzt wird. Heute kennt man eine Reihe von Modellen für solche nichteuklidischen Geometrien, die eine sinnvolle Interpretation innerhalb der Welt unserer Anschauung ermöglichen. Bolyai und Lobatschewski leiteten alle wichtigen geometrischen Eigenschaften her, wenn zu einer vorgegebenen Geraden mehr als eine Parallele durch einen Punkt außerhalb der Geraden verläuft. Zwei besonders wichtige dieser Eigenschaften sollen hier angegeben werden, weil sie den Kontrast zur euklidischen Geometrie deutlich machen:

Die Winkelsumme im Dreieck beträgt weniger als 180°.

Allein aus der Größe der Winkel im Dreieck ergibt sich dessen Flächeninhalt (es gibt also keine ähnlichen Dreiecke verschiedener Größe).

Diese beiden Eigenschaften haben eine Entsprechung in der Kugelgeometrie: Dort beträgt die Winkelsumme im Dreieck mehr als 180°; die zweite Eigenschaft gilt unverändert.

Auch Carl Friedrich Gauß hat Grundzüge der nichteuklidischen Geometrie entwickelt, aber diese nicht veröffentlicht. Er sah voraus, dass die Zeit für eine Anerkennung dieser Ideen nicht reif war. Wie recht er hatte, wird durch die Erfahrungen Bolyais und Lobatschewskis bestätigt. Beide fanden zu ihren Lebzeiten keine nennenswerte Resonanz für ihre neue Geometrie. Da die euklidische Geometrie im Alltag und in der wissenschaftlichen Praxis außerordentlich erfolgreich war, wurde vor allem bezweifelt, dass es eine reale Entsprechung einer nichteuklidischen Geometrie geben könne. Insbesondere glaubte man allgemein, dass unser Universum ein dreidimensionaler euklidischer Raum sei. Der Wert der nichteuklidischen Geometrie für die Physik wurde erst mit der Entwicklung der Relativitätstheorie erkannt. - Während Lobatschewski den Spott seiner Zeitgenossen gelassen ertragen konnte, da er ein ansonsten renommierter Mathematiker in höchsten akademischen Ämtern war, litt Bolyai sehr unter mangelnder Anerkennung, dies war möglicherweise der Grund für seine psychische Erkrankung.

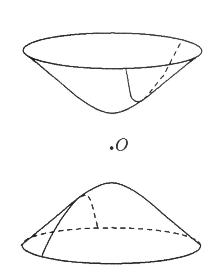
Eine Veranschaulichung einer nicht-euklidischen Geometrie kann u.a. auf der Oberfläche eines Rotationshyperboloiden gegeben werden. Dieser entsteht, indem man beide Äste einer Hyperbel (z.B. x² - y² = 1) um die x-Achse rotieren lässt und so eine Fläche im dreidimensionalen Raum erhält. In der Skizze sieht man diese Fläche mit O als Koordinatenursprung und der x-Achse als der Senkrechten. Die "Geraden" auf dieser Fläche sind die Schnittlinien der Ebenen durch O mit der Fläche. Eine solche Gerade sieht man auch in der Skizze. Es lässt sich nachweisen, dass in diesem Modell alle Sätze der euklidischen Geometrie gelten, mit Ausnahme derjenigen, die vom Parallelenpostulat abhängen, denn auf dem Rotationshyperboloiden hat eine Gerade viele Parallelen durch einen Punkt außerhalb der Geraden.