
Italien 2011 Michel 3466
Goldener Zirkel
Diese italienische Briefmarke zeigt ein mathematisches Instrument: den Goldenenen Zirkel, der in der Geometrie, der Kunst, der Architektur und im Design Anwendung findet. Mit ihm lassen sich u.a. Strecken im Verhältnis des Goldenen Schnitts teilen; dieses Verhältnis findet man ebenfalls im Design der Briefmarke.
Der Goldene Zirkel ist das Emblem eines bedeutenden Preises für Industriedesign, des Premio Compasso d'Oro (dt. Preis Goldener Zirkel), der ca. alle 2 - 4 Jahre vom italienischen Verband für Industriedesign Associazione per il Disegno Industriale (ADI) vergeben wird. Diesem Preis ist die Briefmarke gewidmet.
Wir wollen nun genau anschauen, was auf der Marke zu sehen ist, und dann die dort verwendeten mathematischen Grundlagen erläutern.
Welche Maße finden sich auf der Briefmarke? Wir sehen ein Rechteck, dessen Höhe wir als \(1\) setzen. Der Designer hat ein Goldenes Rechteck gezeichnet, also die Goldene Zahl \(\Phi\) als Breite des Rechtecks gewählt, siehe Bild 1.
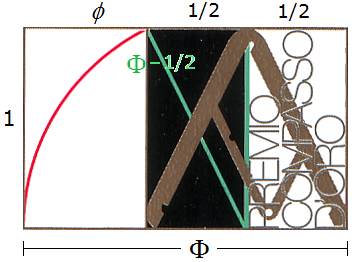
Bild 1 Streckenlängen auf der Briefmarke
Das große Rechteck in Bild 1 ist zusammengesetzt aus einem kleinen Rechteck (links) und einem Quadrat der Seitenlänge \(1\) (rechts, schwarz und weiß). Das kleine Rechteck hat dann die Breite \(\phi=\Phi-1\) . Hier sind die Definitionen von \(\Phi\) und \(\phi\) : \[\Phi~=~\frac{1}{2} (\sqrt{5}+1)~\approx~ 1,618~~~~~~~~~~\phi~=~\Phi-1~=~\frac{1}{2}(\sqrt{5}-1)~\approx~0,618\] Das Quadrat ist halbiert; jede Hälfte nimmt einen der äußeren Schenkel des Zirkels auf. Das schwarze Rechteck in der Mitte hat also die Maße \(1 \times 1/2\) ; daraus ergibt sich die Länge der grünen Diagonalen: \[\text{Diagonale:}~~~\frac{1}{2}\sqrt{5}~=~\Phi-\frac{1}{2}~=~\phi+\frac{1}{2}~\approx~1,118\] Da \(1/\Phi~=~\phi\) , zeigt Bild 1 eine Standardkonstruktion für die Goldene Zahl: Die Seitenlängen des linken Rechtecks stehen im Verhältnis des Goldenen Schnitts, also Höhe/Breite\(~=~\Phi\) ; setzt man an die längere Seite ein Quadrat an, so erhält man wieder ein Rechteck in diesem Verhältnis, also Breite/Höhe\(~=~\Phi\) .
Nun schauen wir uns den Zirkel genauer an. Bild 2 zeigt einen leicht veränderten Ausschnitt der Marke. Wir sehen einen Zirkel mit seinem Gelenk am oberen Bildrand, an dem zwei kleinere Teile mit drei Gelenken befestigt sind. Die Gelenke sind als blaue Punkte markiert. Wir werden noch sehen, dass der Zirkel beweglich ist, weil die blauen Punkte ein Parallelogramm bilden.


Bild 2 Gelenke des Zirkels Bild 3 Teilung der Zirkelöffnung nach dem Goldenen Schnitt
In Bild 3 sehen wir die Funktion des Goldenen Zirkels: Die beiden äußeren orangenen Punkte sollen die Endpunkte einer Strecke markieren. Der Zirkel wird flach auf die Unterlage gelegt und so weit geöffnet, dass diese Punkte in den "Augen" unten an den Schenkeln (auf der Marke als kleine Aussparungen zu erkennen) sichtbar werden. Der mittlere orangene Punkt teilt dann die Strecke im Goldenen Schnitt: (lange Teilstrecke links):(kurze Teilstrecke rechts)\(~=~\Phi\) ; Gesamtstrecke:(lange Teilstrecke links)\(~=~\Phi\) . Der Teilungspunkt ist auf der Marke als offenes "Auge" zu sehen, durch das man einen Stift führen kann.
Der Goldene Zirkel ist also ein mathematisches Werkzeug, dessen mathematische Grundlagen nun untersucht werden sollen. Zunächst ist festzuhalten, dass der Goldene Zirkel einen Spezialfall unter den Proportionalzirkeln darstellt. Wie wir sehen werden, kann man für jedes beliebige Teilungsverhältnis der Strecke zwischen den Schenkelenden einen passenden Zirkel bauen. Alle diese Zirkel bilden die Familie der Proportionalzirkel. Dabei variieren die technischen Ausführungen dieser Zirkel stark; wir wollen hier bei der Grundform bleiben, wie sie auf der Briefmarke für den Spezialfall des Goldenen Schnitts zu sehen ist, aber das Teilungsverhältnis als beliebig ansehen. In Bild 4 ist ein Proportionalzirkel geometrisch abstrahiert dargestellt. Die schwarzen Strecken stellen die vier Einzelteile des Zirkels dar. In Grün ist die zu teilende Strecke auf der Unterlage eingezeichnet.
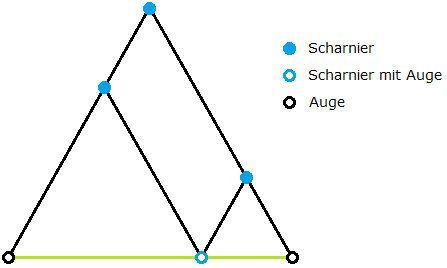
Bild 4 Geometrisches Schema eines Proportionalzirkels
Nun stellen sich mehrere mathematische Fragen: Warum ist der Zirkel beweglich? Liegt das "Scharnier mit Auge" immer auf der grünen Strecke? Wie funktioniert die Streckenteilung in einem vorgegebenen Verhältnis? Um diese Fragen zu beantworten, schauen wir uns an, wie ein Proportionalzirkel konstruiert wird. Bild 5 hilft uns bei dieser Konstruktion.
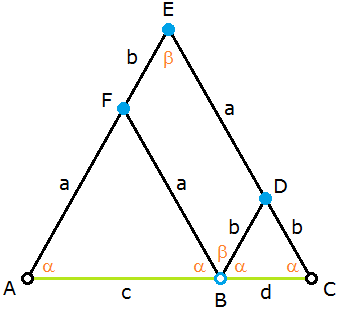
Bild 5 Geometrisches Schema eines Proportionalzirkels
Die Konstruktion eines Proportionalzirkels beginnt wie bei einem normalen Zirkel mit zwei gleich langen Schenkeln \(\text{EA}\) und \(\text{EC}\) (siehe Bild 5); der Einfachheit halber soll die Schenkellänge \(1\) betragen. Dann wird das gewünschte Teilungsverhältnis \(a:b\) vorgegeben, das dann wie in Bild 5 auf die Schenkel übertragen wird. Will man z.B. später mit dem Zirkel Strecken halbieren, wählt man \(a=1/2\) ; will man von Strecken links (rechts) ein Drittel abtrennen, wählt man \(a=1/3 ~~(a=2/3)\); will man den Goldenen Schnitt wie auf der Briefmarke durchführen, wählt man \(a=\phi\) . Diese Teilung der Schenkel führt auf die Teilungspunkte \(\text{F}\) und \(\text{D}\) in Bild 5.
Nun werden Stücke der Länge \(a\) (bei \(\text{F}\) ) bzw. \(b\) (bei \(\text{D}\) ) mit Scharnieren eingehängt; diese Stücke werden an ihren freien Enden mit einem Scharnier verbunden (Punkt \(\text{B}\) ).
Es soll gezeigt werden:
- Der Zirkel ist mit seinen vier Scharnieren beweglich, d.h. der Winkel \(~\beta~\) bei \(~\text{E}~\) kann alle Werte in \(~(0°,~180°)~\) annehmen, und die Strecke \(\text{AC}\) kann alle Längen von \(0\) bis \(2\) annehmen.
- \(\text{B}\) liegt auf der Strecke \(\text{AC}\) .
- \(c:d = a:b\)
Beweise:
\(\text{BDEF}\) ist ein Parallelogramm, da je zwei gegenüberliegende Seiten die gleiche Länge haben. Parallelogramme sind frei verschieblich (alle Winkel können Werte zwischen \(0°\) und \(180°\) annehmen); daraus folgt die Beweglichkeit des Zirkels.
Es folgt: die Winkel bei \(\text{E, F}\) und \(\text{D}\) (genauer: die Winkel \(\text{CEA, BFA}\) und \(\text{CDB}\)) sind gleich (\(~\beta~\) in Bild 5). Also sind \(\text{ACE, ABF}\) und \(\text{BCD}~\) ähnliche Dreiecke (gleichschenklig mit identischem eingeschlossenem Winkel).
\(\text{B}\) liegt auf der Strecke \(\text{AC}\) , denn benennt man die Winkel des großen Dreiecks \(\text{ACE}\) mit \(~\alpha, \alpha, \beta~\), so ergibt die Addition der Winkel bei \(~B~:~~2\alpha + \beta=180°\).
Nun folgt aus den Strahlensätzen: \(~c:a=(c+d):(a+b)~~~~\Rightarrow~~~~c \cdot a + c\cdot b = c\cdot a + a\cdot d~~~~\Rightarrow~~~~c:d = a:b~\).
Welche geometrischen Aufgaben lassen sich mit dem Proportionalzirkel (insbesondere mit dem Goldenen Zirkel) lösen? Bild 6 zeigt nur den unteren Teil von Bild 5, und darunter drei mögliche Wege:
- Teilung von \(~\text{AC}~\) in \(~\text{AB}~\) und \(~\text{BC}~\) im Verhältnis \(~c:d=a:b~\)
\(\rightarrow\) Goldener Schnitt (\(~a=\phi~\)): \(~~a:b=\Phi~~~\Rightarrow~~~c:d=\Phi,~~(c+d):c=\Phi\)
- Verlängerung von \(~\text{AB}~\) auf \(~\text{AC}~\) mit Streckungsfaktor \(~1/a~~~\rightarrow~~~c+d=c/a~\) (hier wird der Stift in das Auge bei \(~\text{C}~\) eingeführt)
\(\rightarrow\) Goldener Schnitt (\(~a=\phi~\)): Streckungsfaktor \(~\Phi~~~\rightarrow~~~c+d=\Phi \cdot c\)
- Verkürzung von \(~\text{AC}~\) auf \(~\text{AB}~\) mit Kürzungsfaktor \(~a~~~\rightarrow~~~c=a(c+d)~\)
\(\rightarrow\) Goldener Schnitt (\(~a=\phi~\)): Kürzungsfaktor \(~\phi~~~\rightarrow~~~c=\phi \cdot (c+d)=(c+d)/\Phi\)
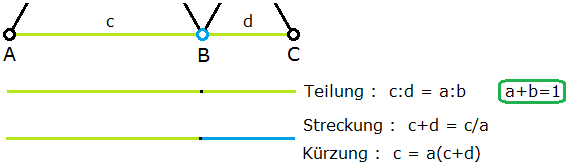
Bild 6 Geometrische Operationen mit dem Proportionalzirkel
Das mathematische Prinzip hinter dem Proportionalzirkel findet sich sehr eindrucksvoll in seiner Weiterentwicklung zum Pantografen. Mit diesem geometrischen Gerät lassen sich Bilder in einen anderen Maßstab übertragen, was in früheren Zeiten u.a. in der Architektur und der Kartografie von großer Bedeutung war.
Der Pantograf ist ein Proportionalzirkel wie in Bild 5, der flach auf dem Papier aufliegt und im Punkt \(~\text{A}~\) drehbar auf der Unterlage fixiert wird. Hält man den Winkel \(~\beta~\) fest, so beschreiben die Punkte \(~\text{B}~\) und \(~\text{C}~\) Kreise um \(~\text{A}~\), wenn das Gerät bewegt wird. Durch Änderung von \(~\beta~\) im Bereich \((0°,180°)\) erreicht man mit \(~\text{B}~\) eine Kreisfläche um \(~\text{A}~\) mit Radius \(~2a~\) und mit \(~\text{C}~\) eine Kreisfläche mit Radius \(~2~\) (wegen \(~a+b=1~\)). Will man eine Figur vergrößert zeichnen, setzt man im Auge \(~\text{B}~\) einen Führungsstift und im Auge \(~\text{C}~\) einen Zeichenstift ein; will man eine Figur verkleinern, vertauscht man diese Stifte.
Bild 7 zeigt (wie in Bild 6) nur die Unterkante \(~\text{ABC}~\) eines Pantografen. Wir sehen drei verschiedene Richtungen dieser Kante (von \(~\text{A}~\) aus gesehen) mit drei verschienenen Öffnungswinkeln \(~\beta~\) (da die Strecken \(~\text{AB}~\) jeweils unterschiedlich lang sind). Es wurde \(~a=2/3~\) gewählt; damit erzielt man eine Vergrößerung aller Längen (nicht der Flächen!) um \(~50\%~\) auf das Anderthalbfache. In Bild 7 soll das grüne Rechteck vergrößert gezeichnet werden. Man fährt es mit dem Führungsstift in \(~\text{B}~\) ab; der Zeichenstift in \(~\text{C}~\) zeichnet dann das blaue Rechteck. Umgekehrt ginge es genauso, wenn man das blaue Rechteck auf \(~2/3~\) der Seitenlängen verkleinern wollte: Führungsstift in \(~\text{C}~\), Zeichenstift in \(~\text{B}~\).
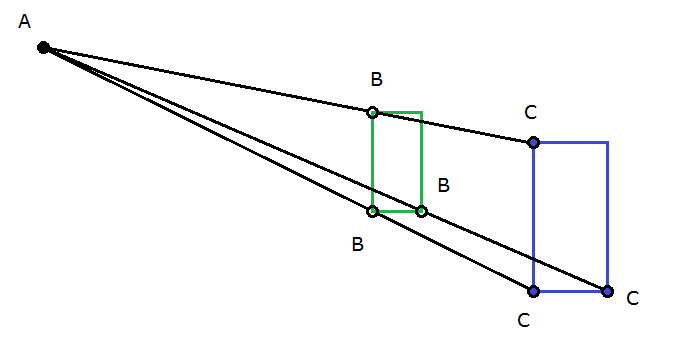
Bild 7 Funktionsweise des Pantografen
Eine Transformation ebener geometrischer Objekte wie in Bild 7 heißt Zentrische Streckung. Sie transformiert diese Objekte in größere oder kleinere geometrisch ähnliche Objekte, ist also eine Ähnlichkeitstransformation. Aus den Strahlensätzen folgt, dass die Zentrische Streckung Geraden parallelverschiebt und winkeltreu ist. Diese Eigenschaften sind für zahlreiche technische Anwendungen erforderlich.
Kategorie: Goldener Schnitt, Goldene Zahl, Fibonacci-Folge