
Liechtenstein 2013 Michel 1662 - 1664
Fibonacci-Zahlen
Das Fürstentum Liechtenstein hat 2013 die Mathematik in bemerkenswerter Weise gefeiert.
Vom 22. November 2012 bis zum 7. April 2013 zeigte das Liechtensteinische Landesmuseum die Mathematik-Ausstellung Geopythafibotonpolyhypotesaeder! Matheliebe. Die Bedeutung einer so umfassenden und hervorragend gestalteten Darstellung der Mathematik für das allgemeine Publikum kann gar nicht genug herausgestellt werden. Besonderes Lob verdient der Brückenschlag von der Mathematik zur Natur und zur Kunst. Die ansprechende Visualisierung mathematischer Sachverhalte mag - so kann man hoffen - der Popularisierung dieser oft wenig geliebten Wissenschaft helfen. Bis Juni 2014 ist diese schöne Ausstellung im Naturkundemuseum Joanneum in Graz zu sehen gewesen.
Initiiert und gestaltet wurde Matheliebe durch Georg Schierscher, der lange Jahre am Liechtensteiner Gymnasium in Vaduz als Mathematiklehrer tätig war. Er wirkte als Kurator der Ausstellung und ist Autor des Katalogs [1]. Dieser Katalog ist ein Prachtband und eine Augenweide. Er zeigt nicht nur die Mathematik von ihrer schönsten Seite, sondern ließe sich auch als Lehrbuch einsetzen (mir gefällt z.B. die didaktische Aufbereitung der Klothoide besonders gut).
Ein kleiner, aber wichtiger Teil der Ausstellung - die Fibonacci-Zahlen - wurde von der Liechtensteinischen Post zum Motiv dreier Briefmarken ausgewählt, die man oben sehen kann.
Über Fibonacci-Zahlen (und deren Zusammenhang mit dem Goldenen Schnitt und der Logarithmischen Spirale) sind auf dieser Website schon mehrere Beiträge erschienen (Briefmarke # 5, Briefmarke # 63, Briefmarke # 75, Problem # 63), so dass es nicht nötig erscheint, die mathematischen Grundlagen hier zu wiederholen.
Was sieht man auf den Marken? Ganz unten rechts stehen die Nennwerte (100, 260, 400 Schweizer Rappen). Davor, in den beiden Fußzeilen, ist der mathematische Gehalt untergebracht, auf den wir noch zu sprechen kommen. Darüber trennt die Goldene Zahl Φ die Wörter Fürstentum und Liechtenstein. Der obere Teil der Marken wird durch ein Spiralraster eingenommen, in das Baumblätter eingepasst sind. Auch darauf wird noch eingegangen.
Auf der linken Marke sieht man die Zahlenfolge 1, 2, 3, 5, 8, ... , 4181 , also die 2. bis 19. Fibonacci-Zahl F(2) ... F(19) , jedenfalls in der am meisten verbreiteten Zählung mit F(1) = F(2) = 1 . Die nächste Fibonacci-Zahl F(20) = 6765 ist aus Platzgründen auf der Marke abgeschnitten. Das Bildungsgesetz ist leicht zu verfolgen: F(n) = F(n-1) + F(n-2) für n ≥ 3 .
Die mittlere Marke wiederholt die Fibonacci-Zahlen und setzt jeweils zwei aufeinanderfolgende von ihnen ins Verhältnis: F(3):F(2) = 2:1, F(4):F(3) = 3:2 usw. bis F(12):F(11) = 144:89 . Folgen würde F(13):F(12) = 233:144 , aber auch das wurde abgeschnitten.
Die rechte Marke enthält nur eine Zahl, nämlich die Goldene Zahl Φ = (1+√5)/2 ≈ 1,61803 . Dies ist der Grenzwert der Brüche auf der mittleren Marke: lim n→∞ F(n+1)/F(n) = Φ .
Dieter Egelriede hat bereits einen sehr detailreichen Artikel über diese Briefmarken veröffentlicht (siehe [2]), auch in der Zeitschrift der Mathematical Study Unit ist ein Beitrag dazu erschienen (siehe [3]). Dieter Egelriede hat viel Geduld und großen Spürsinn bewiesen; er hat sich nämlich die Mühe gemacht, alle Zahlen zu überprüfen und hat tatsächlich zwei Fehler in der Darstellung von Φ aufgedeckt: Die 31. Nachkommastelle (eine 6) fehlt, und die letzte abgedruckte Ziffer muss eine 7 (statt 1) sein.
Der Hintergrund der Blätter ist ein Raster aus Kreisen, Geraden und Spiralen. Die stilisierten Blätter, die dem Raster überlagert sind, haben ihre Spitzen in Schnittpunkten des Rasters. Diese Darstellung folgt dem Entwurf von Martin Hess aus seinem Buch Formvollendet [4]. Das Muster soll auf den Briefmarken möglicherweise den Zusammenhang zwischen Mathematik und Natur illustrieren, der in der Botanik durch das Auftreten der Logarithmischen Spirale augenfällig wird. (Außerdem ist die Goldene Spirale, die sich von der Goldenen Zahl Φ herleitet, ein Spezialfall der Logarithmischen Spirale; damit wäre die Brücke zu den Zahlen auf den Briefmarken geschlagen.) Falls das so beabsichtigt war: Es ist leider nicht ganz geglückt, da die dargestellten Spiralen keine Logarithmischen Spiralen sind. Schon in [4] stimmen die Proportionen nicht, wenn man Logarithmische Spiralen unterstellt (aber auch nicht für andere "regelmäßige" Spiralen), und der Grafiker Hans Peter Gassner aus Vaduz hat zwar in seinem Layout für die Marken die Vorlage von Hess nicht originalgetreu übernommen, aber er hat die korrekten Proportionen ebenfalls nicht getroffen. Hess ist in seiner Beschreibung auch vorsichtig und erwähnt die Logarithmische Spirale nicht; er schreibt lediglich: "Pflanzenblätter und Mathematik: Geometrische Formen in der Natur am Beispiel von Pflanzenblättern. Fotos von Naturblättern wurden in lineare Darstellungen umgesetzt, diese dann abstrahiert, symmetrisiert und auf die relevanten Verästelungen reduziert. Die abstrahierten Blätter wurden in ein Polarkoordinatensystem mit Spiralraster eingezeichnet, um ein Konstruktionsmuster der Blätter zu erstellen. Hierbei kam es nicht darauf an, möglichst genau an das Naturblatt heranzukommen, sondern vielmehr ein Idealblatt zu erhalten."
Was an der Darstellung nicht stimmt, zeigt sich, wenn man die Entstehung der Grafik rekonstruiert. Vom Mittelpunkt gehen 36 Strahlen aus, jeweils im Abstand von 10° . Diese werden geschnitten von mehreren Kreisen in Mittelpunktslage. Durch die Schnittpunkte verlaufen 72 Spiralarme. Will man sich ein eigenes Bild für den Fall verschaffen, dass es sich um Stücke der Logarithmischen Spirale handelt, macht man den Ansatz r = d·eb·φ für die Polarkoordinatendarstellung der Spirale ( r ist der Abstand eines Kurvenpunkts vom Koordinatenursprung; φ ist der zugehörige Winkel, gemessen von der positiven Richtung der waagerechten Achse im Gegenuhrzeigersinn). Die Konstante d ist nur ein Proportionalitätsfaktor, und da auf den Marken kein Maßstab angegeben ist, kann d = 1 gesetzt werden. b ist zunächst frei wählbar, aber wir werden noch sehen, wie sich b aus den Kreisen und Geraden ergeben müsste.
Wir beginnen mit dem Spiralarm, der nach links gekrümmt ist und im obersten Punkt der Grafik endet. Sein genauer Anfangspunkt ist auf den Marken nicht erkennbar (und für das Weitere auch nicht so wichtig). Hier soll er bei einem Winkel von -40° liegen, so dass der ganze Spiralarm den Bereich [-40°, +90°] überstreicht. Das obere Ende dieses Spiralarms kann man ganz gut auf der rechten Marke erkennen.
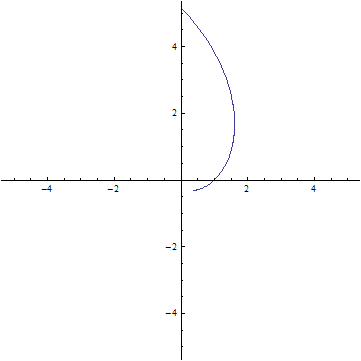
Als nächstes zeichnen wir 36 Geradenstücke ein, die alle radial vom Koordinatenursprung wegzeigen. Ihre Anfangspunkte liegen auf dem Kreis, auf dem auch der Anfangspunkt der Spirale liegt; das gilt analog auch für die Endpunkte. Der Anfangspunkt der Spirale ist also gleichzeitig der Anfangspunkt des Geradenstücks bei -40° , der Endpunkt der Spirale ist auch der Endpunkt des Geradenstücks bei +90° . Es zeigt sich eine charakteristische Eigenschaft der Logarithmischen Spirale: Die Schnittwinkel α der Spirale mit den Geraden sind alle gleich, nämlich α = arccot b .
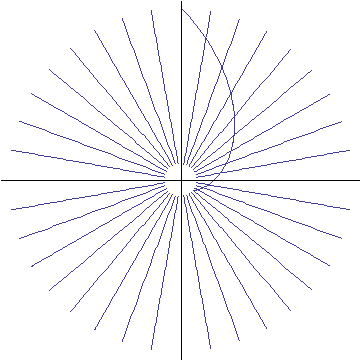
Nun verschiebt man den Spiralarm durch Rotation wiederholt um 10° und erzeugt so 36 Spiralarme, deren Anfangs- und Endpunkte wieder jeweils auf einem der 36 Strahlen liegen.
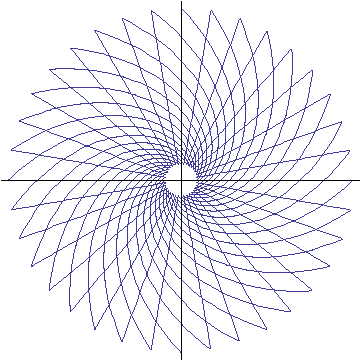
Durch die Schnittpunkte der Spiralen mit den Geraden werden nun 14 Kreise gezeichnet. Auch die Schnittwinkel β der Spirale mit den Kreisen sind alle gleich, nämlich β = arctan b = 90° - α .
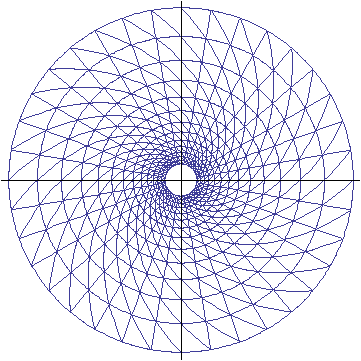
Zuletzt werden noch die 36 rechtsgekrümmten Spiralarme eingezeichnet, die durch die bereits vorhandenen Anfangs-, End- und Schnittpunkte verlaufen:
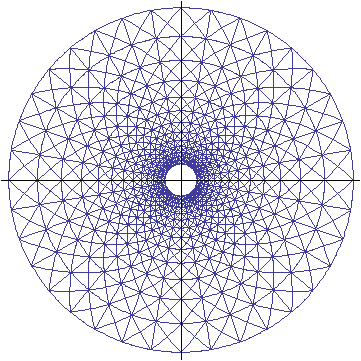
Nun hat man ein Bild, das auf den ersten Blick den Darstellungen in Hess' Formvollendet und auf den Briefmarken entspricht. Es wurde b = 1,045 gewählt, was zu einem Schnittwinkel der Spiralen mit den Geraden von α = arccot b ≈ 43,74° und mit den Kreisen von β = arctan b ≈ 46,26° führt. Dass genau 14 Kreise gezeichnet wurden, hängt mit dem Startpunkt des ersten Spiralarms zusammen; dessen Winkel von -40° wurde gewählt, um die innere (leere) Kreisfläche zu erzeugen, die auf allen Marken (schwach) erkennbar ist, am besten auf der linken Marke.
Nun folgt aber aus dieser Darstellung, dass die Schnittpunkte auf den Geraden in einer geometrischen Folge liegen müssen; genauer: Der Abstand eines Schnittpunkts zum Koordinatenursprung ist eb·k·π/18 , da π/18 (im Bogenmaß) einem Winkel von 10° entspricht; k läuft ganzzahlig von -4 bis 9 ; die Abstände zweier benachbarter Schnittpunkte auf einer der Geraden stehen somit im konstanten Verhältnis eb·π/18 ≈ 1,2 . Ein konstantes Verhältnis ist in Formvollendet und auf den Briefmarken auch nicht annähernd festzustellen; die von den Grafikern gewählten Verhältnisse erscheinen regellos. Man hat den Eindruck, dass zunächst die Kreise (recht willkürlich) gezeichnet wurden und dann die Spiralarme durch die Schnittpunkte der Kreise mit den Geraden gelegt wurden. Jedenfalls sind die Spiralen keine Logarithmischen Spiralen, und die Hinweise in [4] und [5] auf mathematische Gesetzmäßigkeiten in der Natur gehen angesichts der Beliebigkeit der dargestellten Spiralen ein wenig fehl.
 Ersttagsstempel mit Goldener Zahl Φ
Ersttagsstempel mit Goldener Zahl Φ
Literatur
[1] Schierscher, Georg: Geopythafibotonpolyhypotesaeder! Matheliebe, Katalog zur gleichnamigen Ausstellung, Verlag Liechtensteinisches Landesmuseum 2012
[2] Egelriede, Dieter: Mathematik aus Liechtenstein, Techno-Thema 69, S. 13, 2013
[3] Mathematical Study Unit: Fibonacci, Golden Ratio, New Issue from Liechtenstein, Philamath 34/4, S. 3, 2013
[4] Hess, Martin: Formvollendet, Verlag Niggli 2005
[5] Liechtensteinische Post: Ausgabeinformation zur Briefmarkenserie, 2013
Kategorie: Zahlen und Zahlsysteme, Berechnung von π
Kategorie: Goldener Schnitt, Goldene Zahl, Fibonacci-Folge